二叉搜索树
数据结构
本篇文章基于《算法 第四版》第三章,二叉搜索树,我们的树节点是这样的:
private class Node {
Key key;
Value value;
Node left;
Node right;
public Node(Key key, Value value) {
this.key = key;this.value = value;
}
public Node(Key key, Value value, Node left, Node right) {
this.key = key;this.value = value; this.left = left; this.right = right;
}
}
其解决的核心任务是用二叉搜索树构建一个符号表,说白了就是TreeMap,其中Key是二叉搜索树进行比较的依据,它的泛型签名为Key extends Comparable<Key>,Value是映射携带的值,没有类型要求。
读者也可以忽略这些琐碎的细节,只考虑核心代码。
需要注意的是,因为是符号表实现,所以树中没有重复元素
测试用例
使用Junit4进行测试,具有以下初始值:
private OrderedST<Integer, String> st;
@Before
public void setup() {
st = new TreeOrderedSTRecursion<>();
st.put(5, "five");
st.put(4, "four");
st.put(0, "zero");
st.put(8, "eight");
st.put(20, "twenty");
st.put(17, "seventeen");
}
获取最小节点
假设min(Node root)方法用来获取二叉树中的最小节点:
- 如果
root没有左子树,那么最小节点就是root - 如果
root具有左子树,那么最小节点是min(root.left)
private Key min(Node root) {
if (root.left == null)
return root.key;
return min(root.left);
}
测试
@Test
public void testMin() {
int minNumber = st.min();
assertEquals(0, minNumber);
}
后面我们的核心算法都将采用递归这种方式对树进行操作
获取最大节点
不解释了,思路同上:
private Key max(Node root) {
if (root.right == null)
return root.key;
return max(root.right);
}
测试
@Test
public void testMax() {
int maxNumber = st.max();
assertEquals(20, maxNumber);
}
floor——获取小于等于key的最大key
假设floor(Key key, Node root)是在根为root的树中获取小于等于key的最大key,如果没有这样的key,返回null,那么:
- 假设
root==null,那么结果为null - 假设
root.key > key,那么结果为floor(key, root.left) - 假设
root.key == key,那么结果为root.key - 否则
root.key < key,那么令rightFloor = floor(key, root.right),结果为rightFloor == null ? root.key : rightFloor
private Key floor(Key key, Node root) {
if (root == null) return null;
if (biggerThan(root.key, key)) return floor(key, root.left);
else if (equalsTo(root.key, key)) return root.key;
else {
Key rightFloor = floor(key, root.right);
if (rightFloor == null) return root.key;
else return rightFloor;
}
}
测试
@Test
public void testFloor() {
assertEquals(5, (int)st.floor(7));
assertEquals(null, st.floor(-1));
assertEquals(0, (int)st.floor(0));
assertEquals(20, (int)st.floor(22));
assertEquals(4, (int)st.floor(4));
}
ceiling——获取大于等于key的最小值
假设ceiling(Key key, Node root)是获得以root为根的树中,大于等于key的最小key,如果没有这样的key,返回null,那么:
- 假设
root == null,返回null - 假设
root.key < key,返回ceiling(key, root.right) - 假设
root.key == key,返回root.key - 否则
root.key > key,此时令leftCeiling = ceiling(key, root.left),返回leftCeiling == null ? root.key : leftCeiling
由于代码和
floor差不多,不贴了
select——选择树中排名为k的key
select(k, Node root)返回以root为根的树中,排名第k的key。书中的实现感觉时间复杂度有点高,它是假设了有一个size(Node root)方法计算该树的节点数,然后令t=size(root.left):
- 如果
root == null,那么返回null - 假设
t > k,那么返回select(k, root.left) - 假设
t == k,那么返回root.key(由于参数k从0开始) - 假设
t < k,那么返回select(k-t-1, root.right)
我感觉这个算法虽然很优雅,很简洁易懂,但它的时间复杂度较高,虽然理想情况下每次取子树时,size操作需要扫描的节点会变少一半,但还是很多,我们在一个原本就有序的树中获取排名为k的元素,为何不利用一下树的有序性?
实际上,书中的每个节点维护了一个属性
N,代表以它为根的子树的节点数,但我没有维护,所以我没法选择这个办法
我们知道,中序遍历就是按顺序遍历二叉树,那么我们直接对二叉树做一个中序遍历,并维护一个计数器,每次遍历到一个节点时就将计数器递增,当计数器的值为k时,该节点就是我们需要的节点:
private void select(int k, Node root, CounterAndResult car) {
if (root == null) return;
select(k, root.left, car);
if (car.count == k) car.result = root.key;
car.count++;
select(k, root.right, car);
}
@Override
public Key select(int k) {
if (k < 0 || k >= size) return null;
CounterAndResult car = new CounterAndResult();
select(k, root, car);
return car.result;
}
这样写虽然少了些优雅(我想用迭代的方式能将代码写的更优雅一点),但是它的性能相较于之前肯定是提高了,毕竟找到节点后,它的右子树还完全没有遍历过,而书上给的开局就遍历了。
当k很大时(大于节点数的一半),我们可以考虑弄一个“反向的中序遍历”,即按照右中左的顺序遍历,这样遍历就是从大到小遍历了,然后找到第size-k-1个元素(第size-k-1大的也就是第k小的)
private void selectReverse(int k, Node root, CounterAndResult car) {
if (root == null) return;
selectReverse(k, root.right, car);
if (car.count == k) car.result = root.key;
car.count++;
selectReverse(k, root.left, car);
}
@Override
public Key select(int k) {
if (k < 0 || k >= size) return null;
CounterAndResult car = new CounterAndResult();
if (k > size() / 2)
selectReverse(size()-k-1, root, car);
else
select(k, root, car);
return car.result;
}
测试
@Test
public void testSelect() {
assertEquals(0, (int)st.select(0));
assertEquals(17, (int)st.select(4));
assertEquals(20, (int)st.select(5));
assertEquals(4, (int)st.select(1));
assertEquals(null, st.select(-1));
}
deleteMin——删除最小元素
删除最小元素的思路很简单,主要是理解其中的递归技巧。
二叉树中最小的元素就是最最最左边的元素,你只需要一直递归的访问左子树直到一个没有左子树的节点t,并删除它。但是,这个最小的节点可能有右子树,你需要使用t.right代替t的位置,说白了就是让t的父节点的左子树等于t.right。
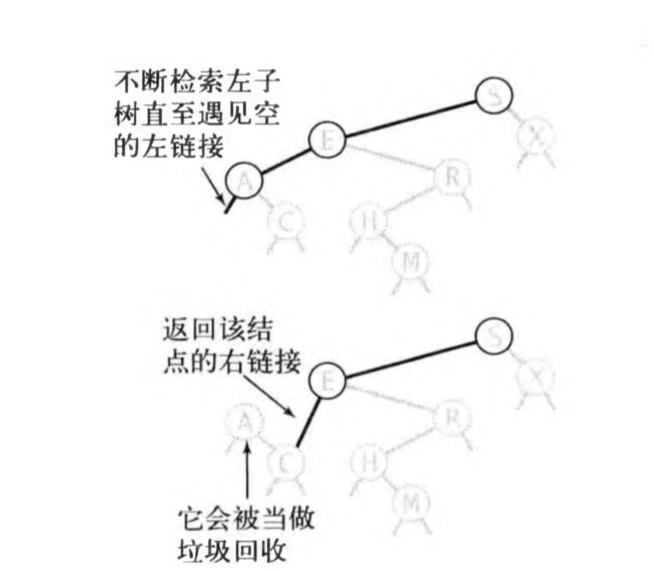
代码很简洁但很巧妙:
private Node deleteMin(Node root) {
if (root.left != null) root.left = deleteMin(root.left);
else return root.right;
return root;
}
deleteMin方法的每一次调用都返回一个值,而在递归调用中,该返回值被设置到当前节点的左子树上:
root.left = deleteMin(root.left);
在正常情况下(当前节点并非最小值的情况),返回值就是传入的参数,所以上面的代码就相当什么也没做,也就是像下面这样:
root.left = root.left;
而在当前节点是最小值的情况下(也就是没有左子树了),那么我们可以对返回值做些手脚,来影响调用栈中的上一层调用的root.left,也就是最小值节点的父节点的left,我们让它等于最小值节点的右子树,也就是最开始所说的思路。相当于:
root.left = root.left.right;
// 原始的root.left由于没人引用了会被GC清理
代码很简单,最主要的是在我们的Node对象没有
parent指针时通过方法调用时的上下层协作,达到用下层返回值来影响上层逻辑的效果
delete——删除元素
删除元素的第一件事就是找到元素,第二件事就是删除它,并继续维持二叉搜索树的性质。
第二件事有点难,说白了就是你要在它的左子树和右子树中找个节点填充它原来的位置,并让二叉搜索树继续保持有序性。待删除节点的左子树中所有元素都比待删除节点小,右子树的所有元素都比待删除节点大,所以,我们只需要将左子树中的最大节点或右子树中的最小节点找出来放上去就好了。我们把删除元素分为四种情况:
- 待删除节点没有左子树和右子树:直接将父节点与它的连接置为null
- 待删除节点有左子树无右子树:将父节点与它的连接置为与它左子树的连接
- 待删除节点有右子树无左子树:将父节点与它的连接置为与它右子树的连接
- 待删除节点有左子树和右子树:从右子树中选出最小的节点m,将父节点与它的连接改为与m的连接,将m的左子树指向待删除节点的左子树,m的右子树指向待删除节点的右子树
private Node delete(Key key, Node root) {
if (root == null) return null;
if (biggerThan(key, root.key)) {
root.right = delete(key, root.right);
} else if (lessThan(key, root.key)) {
root.left = delete(key, root.left);
} else {
size--;
if (root.right == null) return root.left;
if (root.left == null) return root.right;
Node t = root;
root = min(t.right);
root.right = deleteMin(t.right);
root.left = t.left;
}
return root;
}
@Override
public void delete(Key key) {
Requirements.notnull(key, "the key should not be null!");
root = delete(key, root);
}
插入/删除
这部分代码比较简单,我之前用迭代实现的,没有用递归,暂时不放上来了。

