TopK问题 二叉堆与优先队列
面临找工作的我不得不重新刷起数据结构与算法......
问题:TopK元素
非常经典的一个问题,就是给你一堆乱序的数,从中找出其中的TopK。
直接查找
假设K为1,那么很容易想到维护一个max变量并扫描所有数,对于每一个数,与这个max变量比较,如果比它大就将它设置给max,很容易想到这种情况下的时间复杂度为O(N),空间复杂度为O(1)
而对于K>1的情况,你可以维护一个topk数组,这个数组中放的就是前k个最大的元素,而对于每一个扫描到的数,如果它比topk数组中的任意一个大,那么就将topk数组中最小的那个替换出去。所以这个算法的时间复杂度为O(KN),空间复杂度为O(K)。
排序查找
先对TopK数组进行排序,排序后截取TopK个元素,按照当前最好的排序算法,时间复杂度为O(NlogN),空间复杂度为O(N),因为排序要把所有元素都加载进内存。
排序算法确实是较快的一个算法,但若数据量过大,造成的内存成本可能无法承受。
虽然我们有外部归并排序这种基于磁盘的排序手法并且在数据库系统中已经大范围应用,但这种算法很难实现,用在TopK这种小问题上太小题大做了
使用优先级队列
假设我们有这样一种数据结构,MinPQ,它有如下API:
MinPQ(int size) 构建一个能容纳size个元素的MinPQ
void insert(E e) 插入一个元素
E min() 获取最小元素
E delMin() 获取并删除最小元素
int size() 获取元素数量
优先级队列能容纳固定数量的元素,并且可以直接删除并返回其中最小的,这很像我们第一个使用数组的解决办法,只不过使用数组时,我们必须通过扫描topk数组来实现将最小的那个元素替换出去,这个操作的时间复杂度是线性的,导致整体的时间复杂度是平方级别的。
也就是说,只要我们能将delMin方法的时间复杂度限制在线性级别以下,我们就能够获得空间复杂度和时间复杂度都优于之前的算法。
int M = Integer.parseInt(args[0]);
MinPQ<Transaction> pq = new BinaryHeapMinPQ(M + 1);
while(StdIn.hasNextLine()) {
pq.insert(new Transaction(StdIn.readLine()));
if (pq.size() > M) pq.delMin();
}
堆
堆是这样一种数据结构,它是一个树形结构,它的每一个节点都比该节点的所有子节点小或大。如果是小,就称为小顶堆,如果是大,就称为大顶堆,而使用二叉树的就称为二叉堆。下图是一个小顶堆:
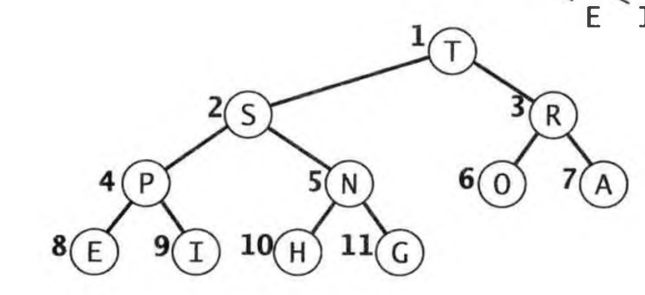
一个小顶堆的的根元素一定是堆中最小的元素,所以这种结构很适合用来实现我们的优先级队列。
我们使用数组来维护二叉堆,对于元素k,它的父节点是k/2,子节点是k*2和k*2+1
我们可以提供上浮和下沉操作来维护堆的有序性:
/**
* 调用该方法时,一般都是数组中的第k个元素可能不在正确的位置
* 它可能比它的子元素大,该方法的作用是让它下沉到正确的位置
*/
private void sink(int k) {
while(k * 2 <= size) {
// 选择两个子当中最小的那个换上来,这样不会出现换上来的那个比另一个大的情况
int toExchIdx = k * 2;
if (toExchIdx + 1 <= size && less(toExchIdx + 1, toExchIdx)) toExchIdx++;
// 如果需要,将最小的那个换上来
if (!less(toExchIdx, k)) break;
exch(toExchIdx, k);
k = toExchIdx;
}
}
/**
* 调用该方法时,一般是该数组中的第k个元素可能不在正确的位置
* 它可能比它的父元素小,该方法的作用是让它上浮到正确位置
*/
private void swim(int k) {
while(k/2 >= 1 && less(k, k/2)) {
exch(k, k/2);
k = k / 2;
}
}
而对于MinPQ的插入操作,我们可以将它插入到数组尾部,也就是二叉堆的最后一个位置,这时它可能顺序不对,调用上浮操作让它上浮到正确位置。
对于MinPQ的弹出最小元素操作,我们可以将树根弹出,并将二叉堆的最后一个元素放到树根位置,此时它的顺序可能不对,调用下沉操作让它下沉到正确位置。
public class BinaryHeapMinPQ<E extends Comparable<E>> implements MinPQ<E> {
private int size;
private final int capacity;
private E[] heap;
public BinaryHeapMinPQ(int capacity) {
this.capacity = capacity;
this.size = 0;
this.heap = (E[]) new Comparable[capacity + 1];
}
@Override
public void insert(E v) {
if (this.size == this.capacity) throw new IllegalStateException("Capacity limited!");
heap[++size] = v;
swim(size);
}
@Override
public E min() {
return heap[1];
}
@Override
public E delMin() {
if (isEmpty()) throw new IllegalStateException("MinPQ is empty now!");
E min = min();
heap[1] = heap[size];
heap[size--] = null;
sink(1);
return min;
}
@Override
public boolean isEmpty() {
return this.size == 0;
}
@Override
public int size() {
return this.size;
}
private void sink(int k) {
while(k * 2 <= size) {
// 选择两个子当中最小的那个换上来,这样不会出现换上来的那个比另一个大的情况
int toExchIdx = k * 2;
if (toExchIdx + 1 <= size && less(toExchIdx + 1, toExchIdx)) toExchIdx++;
// 如果需要,将最小的那个换上来
if (!less(toExchIdx, k)) break;
exch(toExchIdx, k);
k = toExchIdx;
}
}
private void swim(int k) {
while(k/2 >= 1 && less(k, k/2)) {
exch(k, k/2);
k = k / 2;
}
}
private boolean less(int i, int j) {
return heap[i].compareTo(heap[j]) < 0;
}
private void exch(int i, int j) {
E tmp = heap[i]; heap[i] = heap[j]; heap[j] = tmp;
}
}
采用优先级队列后,算法的时间复杂度为O(NlogK),空间复杂度为O(K)。
时空复杂度总结
| 算法 | 时间复杂度 | 空间复杂度 |
|---|---|---|
| topk数组 | \(O(KN)\) | \(O(K)\) |
| 排序 | \(O(NlogN)\) | \(O(N)\) |
| 优先队列 | \(O(NlogK)\) | \(O(K)\) |
综合来说,优先队列的表现最好。
堆排序
堆排序是一种非原地排序算法,思路是构建一个大小为N的堆,将原数组所有N个元素插入,并依次拿出最小的。
堆排序的时间复杂度即使在最坏情况下也只需要\(2NlogN\),在算法分析中,这个2是可以省略的,这已经超越了快速排序在最坏情况下的时间复杂度,而且它需要的额外空间也很稳定,只是\(O(N)\)(快速排序不需要额外空间)。

