CSAPP(二)下——浮点数表示 信息的表示和处理
二进制小数#
先来看看十进制小数的表示法:
上面的十进制小数的值为:
相应的,二进制也一样:
上面二进制小数的值为:
受这个启发,我们可以这样在计算机中表示一个小数,假设我们使用4位表述一个小数,那么我们可以让前两位代表整数位,后两位代表小数位。
然而,几乎没人使用固定的整数和小数位数来在计算机中表示小数,原因在于,假设你运算1.0/8.0,按道理来说,它们两个都可以使用4位整数部分和1位小数部分表示,所以,使用5位完全可以分别表示这两个数,但是它们运算过后的结果0.125却没法使用它们的位模式来表示。
固定的整数和小数位数相当于在给定的位长度下将小数点的位置固定了,由于固定后产生的种种不便,所以小数点不固定的小数表示方法诞生了,这就是浮点数。
初学c语言时好奇,为什么小数要叫浮点数,现在明白了,就是小数点的位置仿佛在所有位之间漂浮,游动。
IEEE表示法#
IEEE的标准浮点数表示法的目标是方便的表示那些值为的数,有点抽象,看个例子
a=10404.0
转换成二进制:10 1000 1010 0100.0
小数点左移13位:1.01000101001000 x 2^13
这就相当于用指数y来控制小数点的浮动,上面的例子中,说明想要得到实际的值,需要将小数点向右移动13位。所以,IEEE把所有的数都标准化成1.xxxxx的格式(并非所有数,只是其中一种情况,稍后会讨论),并且由于1是固定的,所以可以省略不计,只记录小数部分,然后再通过记录一个指数来控制小数点移动的多少,这个指数也可以是负的,代表向左移动呗。
格式定义#
上面只是对IEEE如何表示浮点数的一个全局的概览,下面来介绍细节,内容稍有些枯燥。
IEEE浮点标准使用来表示一个浮点数值,其中有三个参数,就相当于上面讲到的小数部分,就相当于要移动的指数,则是用来控制该浮点数的正负。
下面是IEEE定义的单精度32位和双精度64位浮点数的位级表示
IEEE为了让这个位级表示能够优雅的进行比较(稍后会看到),将位级表示中的三个部分按如下方式映射到上面公式的三个参数中:
s位,直接映射到参数exp位,它是一个正整数,表示范围从全0到全1,它映射到指数参数,但并不是直接映射,并且在不同的情况下映射规则不同,稍后会说frac位,它映射到小数部分参数,同样在不同情况下有不同的映射规则。
规格化的值#
规格化的值是IEEE浮点数的第一个格式,除了不能表示非常靠近0的小数、正负无穷和Nan(Not a number)之外,它负责表示其它的所有小数。
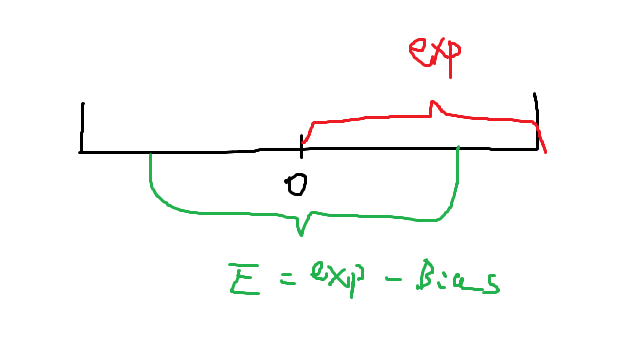
如果exp不是全零或全1,那么当前浮点数就处在规格化模式下,。
Bias是什么?上面说了,将被映射到指数上的exp是一个正整数,但是,如果你想表示1以内的小数,你需要乘以一个负指数,所以你需要做些什么让完全在数轴上0的右侧的exp左移,变成有符号的可负可正的整数,并且最好这个移动是均匀的,即让正数和负数差不多一边多。如果在单精度情况下,exp是8位,那么它能表示的值在0~255之间,,这样就能把完全为正整数的exp拉一半儿到负数那边了。
注意:在
exp长度为时,
为什么
exp字段没有使用补码数而是使用这种方式来表示有符号数?为了使浮点数能够直接作比较还有在非规格化值与规格化值之间平滑过渡。稍后就会看到。
在规格化情况下,,即frac表示小数部分,并且小数点前面有个隐含的1。
总结一下规格化模式下的和:
规格化值示例#
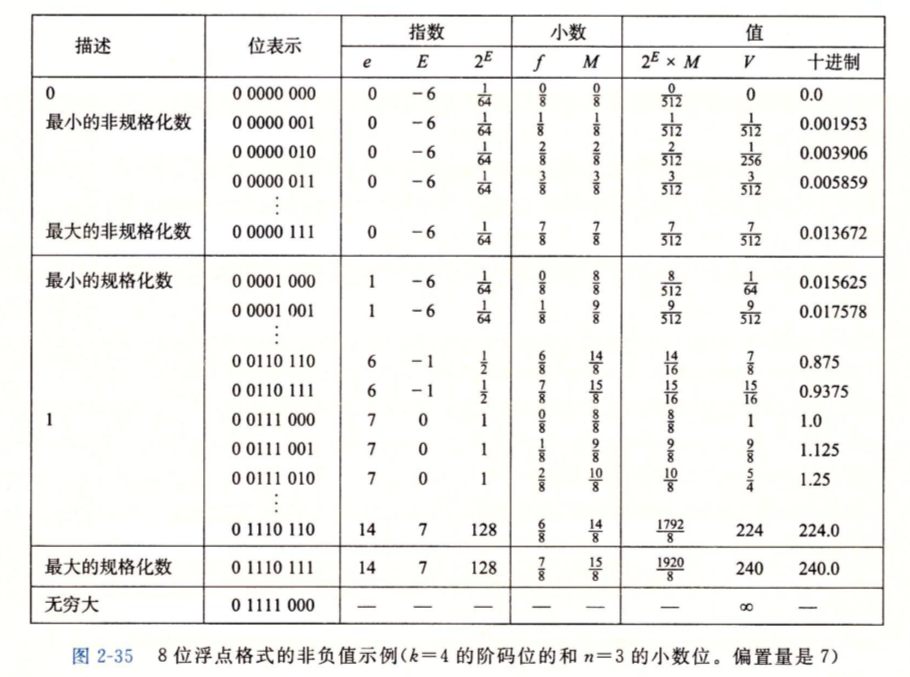
请计算下面的8位浮点值,其中exp长度为4,m长度为3
s exp m
0 0001 001
非规格化的值#
当exp全为0时,该浮点数是非规格化值,非规格化值主要用于表示一些非常接近于0的数,因为毕竟规格化值中的M需要加个1。
非规格化时,,。
非规格化值示例#
s exp m
0 0000 111
特殊值#
当exp全为1,frac全为0时,代表无穷,时是正无穷,是负无穷。当frac非0时,代表Nan。
运算示例#
下面的一个运算示例可以手动算一下,大概就能明白这里面的运算过程了
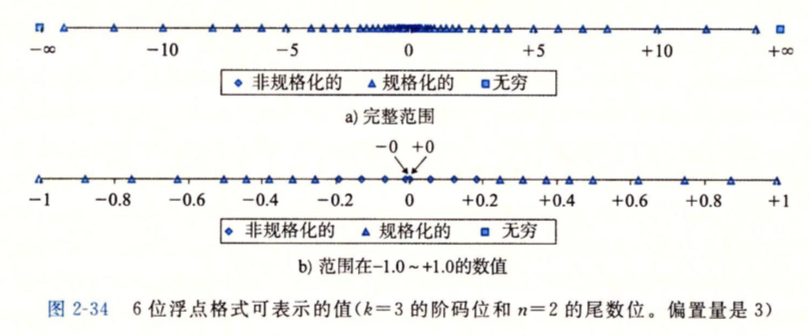
同时也能发现,规格化值下,每当+1,能表示的两个数之间的间隔就大一倍,在非规格化与最初的规格化时,它们的间隔相等。非规格化数值可以平滑的过渡到规格化数值。
IEEE浮点数的特性#
- 浮点数0的位表示与整数0的位表示相同
- 由于浮点数从小到大也是从位全0到位全1表示的,所以它可以直接进行比较(除了负无穷之外)
- 由于采用的编码格式,所以它有+0和-0
关于浮点数的一些思考#
下面的一些思考是我自己瞎琢磨的,感觉能加深对IEEE浮点数工作方式的理解,如果有错误要告诉我o~
假设frac为k位,并且我们忽略负数的情况,即
- 当
exp保持不变时,后面乘以的指数是一个常数,所以。M即frac所表示的内容,不管是在非规格化还是规格化模式下,每次frac增加1,frac中得到的数字都只增加了,这是两个紧挨着的能表示的浮点数之间的间隔。然后这个间隔会被常数放大或缩小,但不论如何,具有同样的的能表示的所有数之间的间隔相同。 - 当
exp+1时,常数等于之前的倍,先别考虑那些特殊情况,只考虑规格化值。所以那些之前的间隔也被扩大了2倍。 - 非规格化扩展到规格化时,虽然的解释和的解释都发生了变化,但IEEE标准巧妙地让非规格化和第一批规格化数具有相同的,所以第一批规格化数之间的间隔和非规格化数之间的间隔相同,并且解释的巧妙变化使得非规格化数能够平滑过渡到规格化数。
- 每轮发生变化,都为能够表示的所有浮点数中贡献了个浮点数,也就是
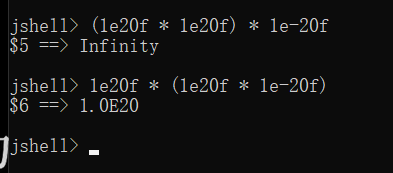
frac那些位中所有能表示的数。 - 所以,能够浮动的小数点只让我们对位的利用率变得更高了,我们实际上还是有很多数没法表示,甚至当越来越大时,每次的放大倍数也越来越大,导致连两个连续的整数都表示不了。这也是为什么
(3.14f + 1e20) - 1e20 = 0,而3.14f + (1e20 - 1e20) = 3.14了。
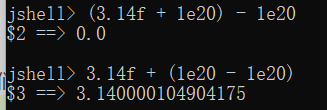
读者不妨想想为什么上面的两个数学上会得到一样结果的表达式在计算机中为什么得到不一样的结果了。
因为,如果先做3.14f + 1e20,将得到很大很大的浮点数,的值也会变得很大,来让小数点疯狂向后移动。增大了,放大倍数就增大了,导致前面的常数3.14直接被埋没在巨大的放大倍数下两数之间的间隔之中,所以导致最终结果是0。而如果你先做后面的减法,这种情况就不会出现。
舍入#
如果你仔细看了上面的那五条,并且你能回答出后面那个问题,你就知道,我们的浮点数设计并不能精确的表示那些间隔之间的每一个小数,所以当一个小数落在间隔之中,我们就要指定一些规则,让它向间隔的某一边靠拢。
以下是四种常见的舍入方式以及它们产生的效果。
向偶数舍入是默认的舍入方式,也是唯一一个需要我们去思考的舍入方式。
为什么向偶数舍入是默认的舍入方式?因为向下舍入,向上舍入和向0舍入都将会在计算平均值时产生一些偏差。如果你使用向下舍入,平均值可能会变得比实际低,如果你使用向上舍入,平均值可能会变得比之前高,而向0舍入只是在正数下的向下舍入,在负数下的向上舍入,对于这种偏差,使用向0舍入不会有什么改观。
向偶数舍入#
向偶数舍入也被称为向最近的值舍入,这两个名字是从两个角度来看这个舍入规则。
先看向最近的值舍入,当遇到1.4,它明显离1最近,那么结果就是1,而1.6,它明显离2最近,舍入结果就是2。
那么向偶数舍入是什么意思?它的意思是说,如果一个数刚好处于间隔中间,比如1.5处于1和2中间,这时候该遵循什么规则,它并不离其中的哪个更近一点儿。这时尊寻向偶数舍入的规则,1不是偶数,所以1.5被舍入到2,对于2.5,3不是偶数,所以2.5也被舍入到2。
所以,这两个名字结合起来才能描述这种舍入方式的运作啊,这名字取的真让人困惑。
向偶数舍入会导致这种正处于中间的值一半向上舍入,一半向下舍入,这样你求平均值时偏差就会变小。(如果你的数据分布正常)
在向某一个小数位舍入时,我们要看的是最低有效位的奇偶,比如下面四组,舍入到2位小数
- 1.2349999 => 1.23
- 1.2350001 => 1.24
- 1.2350000 => 1.24
- 1.2450000 => 1.24
当用在二进制上时,我们可以认为0是偶数,1是奇数,我们也要舍入到两位小数
- 10.11100 => 11.00
下面精确到小数点后一位
- 10.011 => 10.1
- 10.010 => 10.0
- 10.110 => 11.0
- 11.001 => 11.0
浮点运算#
对于浮点运算,IEEE规定对于两个浮点值看成实数,然后对于它们的某个运算,得到的结果将是,也就是对实际的精确结果进行舍入后的结果。
可是在计算机中,我们永远不可能有无限的位来表示一个小数,所以浮点运算单元的设计者通常都会通过一些技巧避免精确值的计算,直接得到舍入后的结果,我们无需考虑具体的实现,只需要知道能得到正确的结果即可。
浮点加法运算#
- 可交换,
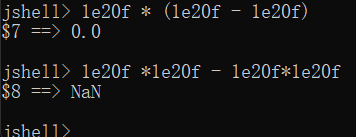
- 不可结合,不一定等于
浮点乘法运算#
参考#
下面是除了原书外的一些其他参考,可能给你带来启发
作者:Yudoge
出处:https://www.cnblogs.com/lilpig/p/16243069.html
版权:本作品采用「署名-非商业性使用-相同方式共享 4.0 国际」许可协议进行许可。
欢迎按协议规定转载,方便的话,发个站内信给我嗷~







【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· winform 绘制太阳,地球,月球 运作规律
· 上周热点回顾(3.3-3.9)