事务的并发控制
前一篇的内容是事务的基本概念,为了保证事务的隔离性,数据库系统需要一定的并发控制机制。这一篇对并发控制机制进行研究,不考虑故障以及故障恢复,把目光放在并发控制上。
基于锁的协议
有并发的地方就有锁,锁的核心原理就是当一方想要访问一个数据项时,先请求获得该数据项的锁,同一时间内只有持有锁的一方可以访问该数据,当访问完成后,释放锁。
锁
有多种多样的锁技术可供我们使用,我们主要考虑两种锁技术
- 共享的(shared):如果事务\(T_i\)持有Q上的共享锁S(shared-mode lock),\(T_i\)可读但不可写Q
- 排他的(exclusive):如果事务\(T_i\)持有Q上的排他锁X(exclusive-mode lock),则\(T_i\)可读可写Q
如果一个事务\(T_i\)请求获得数据项Q上的锁A,此时事务\(T_j(i\neq j)\)已经持有数据项Q上的锁B了,如果此时\(T_i\)仍可立即获得锁,那么称锁A与锁B是相容的(compatible)。
共享锁(S)和排他锁(X)的相容性如下
| S/X | S | X |
|---|---|---|
| S | true | false |
| X | false | false |
意思就是,只有共享锁和共享锁是相容的,一个数据项上只能同时存在多个共享锁,而排他锁无论和共享锁还是排他锁都不相容,一个数据项上如果存在排他锁,那么此时这个数据项上一定只有这一个锁。
我们假设,一个事务可以通过lock-S(Q)申请数据项Q上的共享锁,可以通过lock-X(Q)申请数据项Q上的排他锁,可以通过unlock(Q)释放数据项Q上的锁。
一个事务想要操作一个数据项,那么必须先持有支持操作类型的锁,如果在这之前该数据项上已经有了一个不相容类型的锁,该事务就必须等待持有锁的对应的事务释放锁才能继续操作。
过早释放锁
一个加锁解锁的思路就是当数据项使用完立即释放锁,这在并发条件下可能会产生不一致状态。

比如如上两个事务,假设A账户初始余额是200,B账户初始余额是100,那么无论怎样进行转账操作,A与B余额之和应该始终是300。
考虑如下的并发调度
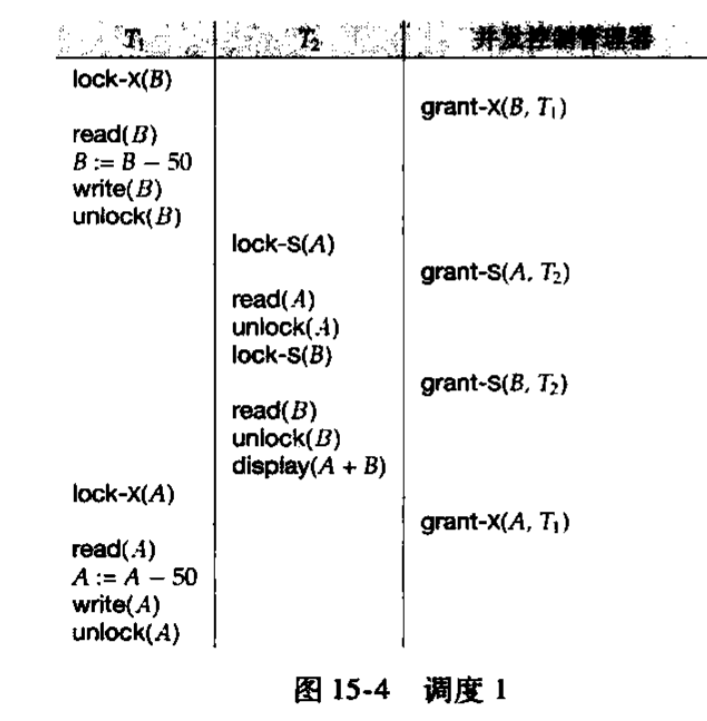
\(T_1\)对B做完扣款操作后立马释放了锁,这时\(T_2\)有可能先执行并且一次性执行完,此时\(T_1\)中的转账操作才完成了一半,所以\(T_2\)将看到不一致的状态,即\(A+B=250\)
死锁
假设有这样的一个调度,它们会产生死锁
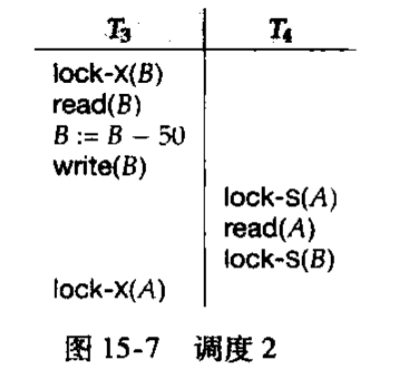
\(T_3\)持有B上的排他锁,\(T_4\)想要获取B上的一个锁只能等待\(T_3\)释放锁才能继续执行。与此同时,\(T_4\)持有A上的共享锁,\(T_3\)想获得A上的排他锁,只有等待\(T_4\)释放锁才能继续执行。
它们互相等待对方释放锁,这时就会陷入无限的等待中。这时必须回滚两个事务中的一个,使另一个可以正常执行。
封锁协议
上面的两个例子说明,释放锁过早和过晚都会产生一些问题,当然过早产生的问题更严重,它已经影响了数据库的一致性。
封锁协议指定了事务何时可以对数据项进行加锁、解锁。它们限制了可产生的调度数目,使那些有问题的调度无法产生。这些调度组成的集合是所有可能的可串行化调度的一个真子集(意思就是保证一致性)。
先学习一些概念:
如果调度S中的事务\(T_i\)在数据项Q上持有A型锁,后来S中的事务\(T_j\)在数据项Q上持有B型锁,并且这两个锁不相容,那么称在调度S中\(T_i\)先于\(T_j\),记作\(T_i\to T_j\)。这意味着在任何等价的串行调度中,\(T_i\)出现在\(T_j\)之前。
当调度S是那些遵从封锁协议规则的事务集的可能调度之一,那么说S在指定封锁协议下是合法的(legal)。
当且仅当一个封锁协议下的所有合法调度都是冲突可串行化的,才称一个封锁协议保证冲突可串行性。
饿死
如果事务\(T_2\)在数据项Q上持有共享锁,\(T_1\)想申请Q上的排他锁,它在等待\(T_2\)释放锁,但在这过程之间,可能有新的事务\(T_3\)来对数据项Q持有共享锁,所以\(T_1\)还要等待\(T_3\)释放锁。
有可能\(T_1\)很久很久也不会得到一个排他锁,因为在\(T_1\)获得锁之前,一直有事务对数据Q持有共享锁。
解决办法是,当一个事务T申请对数据项Q加上M类型的锁时,满足下面两个条件才授予:
- 数据项Q上没有与M不相容类型的锁
- 没有一个事务T'在T之前就等待对数据项Q加锁(主要是这条保证了饿死状态不会发生)
两阶段封锁协议
两端封锁协议保证可串行性。它将加锁和解锁分为两部分
- 增长阶段:只能加锁不能解锁
- 缩减阶段:只能解锁不能加锁
所以事务一旦开始进行了解锁操作,就不能再进行任何加锁操作。
\(T_3,T_4\)符合两段封锁协议


\(T_1,T_2\)不符合两段封锁协议

思考下,这个封锁协议是如何解决不一致的问题的。一旦事务开启缩减阶段时,它就无法再申请排他锁来对数据项进行修改,甚至无法申请共享锁重读一个数据项。也就是说数据项的读取和修改一定在增长阶段和缩减阶段之间,而这个阶段中,其他事务也无法对当前事务已经持有锁的数据项进行修改。
一个事务增长阶段的结束位置(最后加锁的位置)称为封锁点,多个事务可以根据封锁点进行排序,这样就产生了一个可串行化调度。
两段封锁协议不保证无死锁。
两段封锁协议不保证无级联,也就是说一个事务失败了,可能产生多个事务的级联回滚。可以通过稍微修改一下两段封锁协议,让任何事务在commit操作之前,不允许释放排他锁。这避免了其他事务读取到修改后未提交的数据,也就避免了级联回滚。这种协议称为严格两阶段封锁协议。
还有一种就是强两阶段封锁协议,它不允许在未提交之前释放任何锁。
锁转换
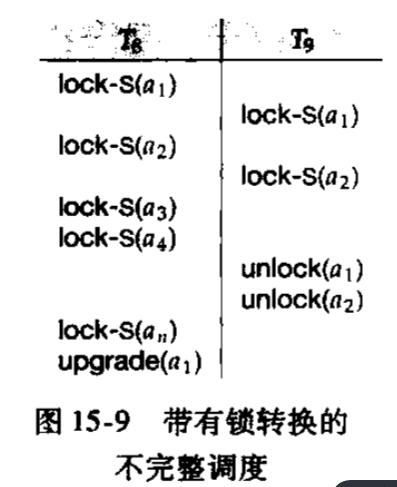
使用两段封锁协议对以下两个事务加锁

\(T_8\)修改数据项\(a_1\),所以我们必须在增长阶段给它加上排他锁,而\(a_2...a_n\)则只需要共享锁。\(T_9\)只需要给\(a_1\)和\(a_2\)加上共享锁即可。这里\(T_8\)和\(T_9\)在数据项\(a_1\)上使用了两个不相容的锁。那么无论如何,这两个事务都会以串行方式执行。
但其实,\(T_8\)只在最后一个指令时对\(a_1\)进行写操作,完全没必要让两个事务串行执行,如果能先让\(T_8\)在\(a_1\)上加一个共享锁,让二者并发执行,当需要写入时再换成排他锁,那么并发度会提高。
所以我们需要一种锁转换机制。使用\(upgrade(Q)\)命令将事务对Q的锁由共享锁升级成排他锁,\(downgrade(Q)\)相反,由排他锁降级成共享锁。
两个命令的操作时机依然受限,\(upgrade\)只允许在增长阶段使用,\(downgrade\)只允许在缩减阶段使用。
如下是使用锁转换时\(T_8\)和\(T_9\)的一个并行调度。
死锁处理
死锁处理主要有两个方法,第一个是死锁预防,第二个是死锁检测。
死锁预防就是使用一些策略来保证系统中永不出现死锁,死锁检测是允许系统中出现死锁,但系统中始终有一个周期执行的算法,它每隔一段时间检测是否存在死锁,如果存在,进行恢复操作。
死锁预防
同时加锁
死锁产生的场景都是这样的:
T1 T2
lock-X(A)
lock-X(B)
lock-X(B)
lock-X(A)
...
多个事务本身是持有锁的,然后它们还尝试去持有其它锁,但它们此时想要获得的锁都被其它事务持有着,所以它们必须全部陷入等待之中。
那让一个事务中的加锁操作同时发生,换句话说,让这些加锁操作变成原子的,要么就全加上,要么就一个都别加,都等着,这问题不就解决了?
T1 T2
lock-X(A)
lock-X(B)
lock-X(B)
lock-X(A)
简单的解决办法一般都有很多缺点
- 当事务没开始执行时一般很难知道都需要对什么数据项加锁
- 数据利用率变低,一些长时间不用到的数据也会在一开始就被加上锁
按次序加锁
按次序加锁给所有数据项排成一个指定的次序,对数据项的加锁必须按次序进行,比如如下会造成死锁的调度,它就不满足按次序加锁,因为\(T_1\)中对数据项加锁的次序和\(T_2\)中的不一致。
T1 T2
lock-X(A)
lock-X(B)
lock-X(B)
lock-X(A)
...
可以修改为
T1 T2
lock-X(A)
lock-X(A)
lock-X(B)
lock-X(B)
...
这样死锁依然不会发生
抢占与回滚
抢占与回滚一般通过给事务分配时间戳来确定系统为了不产生死锁该拒绝哪一个事务的加锁操作,当事务的加锁操作被拒绝时事务就要回滚重启,或以失败告终。
- wait-die:当\(T_i\)想要申请的锁被\(T_j\)持有,仅当\(T_i\)的时间戳小于\(T_j\)时允许\(T_i\)等待,否则直接回滚\(T_i\)
- wound-wait:当\(T_i\)想要申请的锁被\(T_j\)持有,仅当\(T_i\)的时间戳大于\(T_j\)时允许\(T_i\)等待,否则直接回滚\(T_j\)
我用一个例子和wait-die算法来说明抢占与回滚的有效性
下面的例子中,事务后面的括号代表系统分配给它们的时间戳
T1(5) T2(10)
// 正常加锁
lock-X(A)
// 正常加锁
lock-X(B)
// T1时间戳小于T2,T1等待
lock-X(B)
// T2时间戳大于T1,T2回滚,T1可以正常执行了
lock-X(A)
...
锁超时
一个简单的死锁解决办法,当申请锁的等待时间超过一个阈值时,自动回滚当前事务
死锁检测与恢复
死锁检测
系统维护一个等待图,\(G=(V,E)\),\(V\)是顶点集,由参与调度的全部事务组成,\(E\)是边集,若图中存在一条边\(T_i \to T_j\),说明\(T_i\)在等待\(T_j\)释放锁。
当等待图中存在环时,发现死锁,这时需要系统采取恢复措施。
死锁恢复
恢复算法一般选择环中的一个或多个事务进行回滚。
系统会选择代价最小的那一个(一些)事务进行回滚,这依赖于多方面的考量,比如:
- 事务使用了多少数据项
- 多少事务需要级联回滚
- 为完成事务还需要使用多少数据项
- 事务已经计算了多久等
- 事务已经回滚的次数(防止总是这一个事务回滚而饿死)
回滚可以使用彻底回滚,就是将整个事务中止并重启,也可以使用部分回滚,就是只回滚到可以解决死锁的位置。部分回滚需要系统提供更多的信息。
多粒度封锁协议
多粒度
迄今为止讨论的都是基于数据项进行加锁,但现实中行级锁,表级锁都有出现,比如我们想对一个表结构进行修改,如果使用基于数据项的粒度进行加锁,那么我们需要对表中的每一个数据项都加锁,这时不如把粒度放宽,针对整张表加锁。
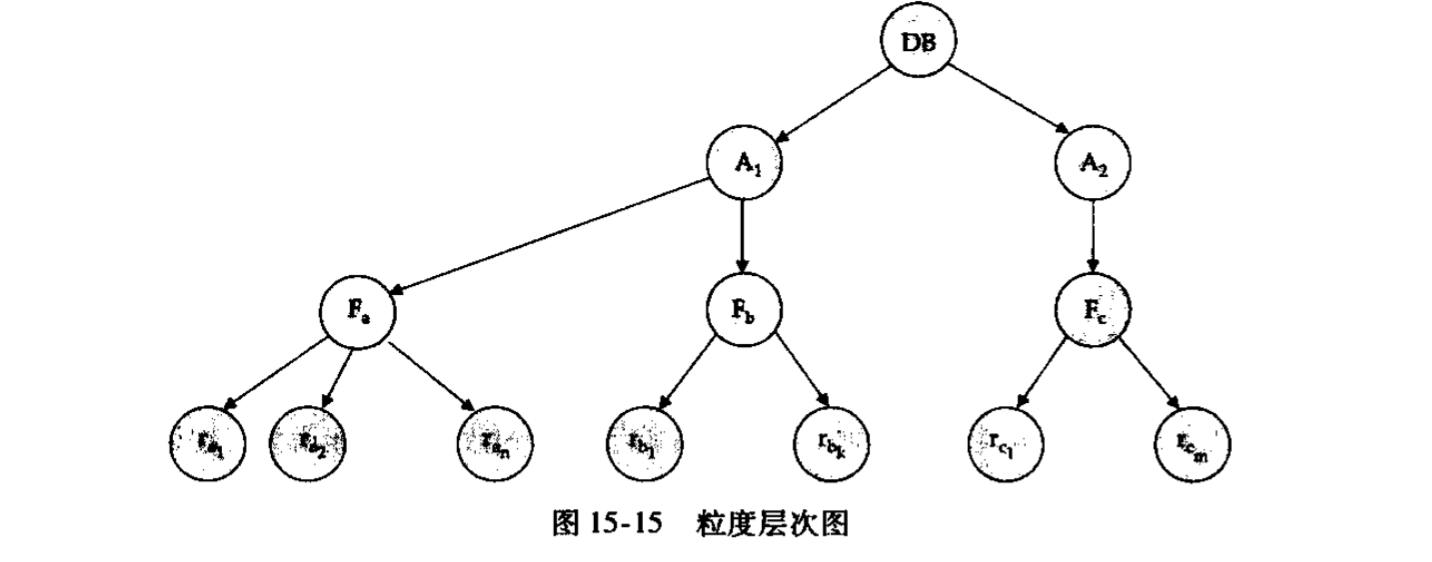
上面分开了许多加锁的粒度,树根是基于整个数据库加锁,下一层是基于数据库中的某些区域加锁,再下一层是基于数据库中的某些文件加锁,再下就是基于文件中的某些记录加锁。我们可以给这些地方加排他锁和共享锁。
如果\(T_i\)给文件\(F_b\)加锁,\(T_j\)此时想给\(F_b\)下的记录\(r_{b_1}\)加锁是不行的,因为\(T_i\)已经锁住了整个文件,但\(r_{b_1}\)上又没有什么能够显示表明它被\(T_i\)锁住了,所以当加锁时需要显式的沿父节点向上找,如果在树的父节点上有锁,那么待加锁的事务必须等待。
反过来考虑,如果\(T_k\)想要给整个数据库加锁,但此时\(T_i\)已经给文件\(F_b\)加上了锁,所以,\(T_k\)不可能成功。所以加锁时不仅要向上找父节点,可能还要遍历整个子树,如果你在根节点上加锁,那么就是遍历整棵树,我们研究多粒度的目标就是不想进行太多操作啊。。。现在反倒更多了。
也看到了,遍历所有父节点比遍历整棵树简单的多,因为父节点能有几个啊。所以我们可以把上面的遍历整棵树问题变成遍历父节点问题。解决办法就是添加意向锁。一个节点上有意向锁,代表这个节点的子节点上有可能有加锁操作。这样如果一个节点要在树底层进行加锁,那么它只需要遍历它的祖先节点并全部加上意向锁就行了。
再考虑\(T_k\)和\(T_i\)的问题,\(T_i\)给文件\(F_b\)加锁,这时\(F_b\)的所有祖先节点上都要有\(T_i\)加的意向锁,也就是\(A_1\)和\(DB\)上,这样\(T_k\)不用遍历整棵树也知道它不能给\(DB\)加锁。
至此我们又多了三种锁:共享型意向锁(intention-shared (IS) mode)、排他型意向锁(intention-exclusive (IX) mode)、共享排他型意向锁(shared intention-exclusive (SIX) mode)。
共享型意向锁代表着它的底层节点上可能显式加锁,但这个显式加的锁只能是共享锁、排他型意向锁代表着这个显式加的锁可以是共享锁和排他锁。共享型排他锁代表着以该节点为根的子树已经显式加了共享锁,并且可能在树的更底层显式的加排他锁。
协议
多粒度封锁协议要求事务\(T_i\)对数据项Q加锁时需要遵守如下规则:
- 事务\(T_i\)必须遵循如下的锁类型相容函数

当存在另一个事务\(T_j\),它已经在数据项Q上加了与\(T_i\)想加的锁类型不相容(对应位置为false)的锁时,\(T_i\)不能立即获得锁 - 事务\(T_i\)必须先封锁树的根节点,并可以加任何类型的锁
- 仅当\(T_i\)对Q的父节点持有
IX或IS型锁时,\(T_i\)才可以在Q上加IS或S型锁 - 仅当\(T_i\)对Q的父节点持有
IX或SIX型锁时,\(T_i\)才可以在Q上加X、IX、SIX型锁 - 仅当\(T_i\)未曾对任何节点解锁时,\(T_i\)可以对节点Q加锁(\(T_i\)采用两段加锁)
- 仅当\(T_i\)不持有Q子节点的锁时,\(T_i\)可以对Q解锁
加锁按照自顶向下的方式(根到叶子),解锁按照自底向上的方式(叶子到根)
基于时间戳的协议
之前讨论的协议都是通过锁。当两个事务面对冲突,它们的次序由哪一个事务先对数据项施加不相容的锁来决定。基于时间戳的协议给出了另一种办法,是在事务执行前先行确定它们在冲突情况下的次序。
时间戳
调度中的每一个事务,在执行之前都会分配一个唯一的时间戳,记作\(TS(T_i)\)。如果在事务\(T_i\)之后又有一个事务\(T_j\)进入系统,则\(TS(T_i) < TS(T_j)\),可以使用以下方法分配时间戳:
- 使用系统时钟
- 使用计数器,每次分配时间戳,计数器自增
系统必须保证,基于该协议产生的调度中,若\(TS(T_i) < TS(T_j)\),则调度等价于某个\(T_i\)在\(T_j\)先前执行的串行调度。
为了实现这一机制,每个数据项Q也必须与两个时间戳相关联:
- \(R-timestamp(Q)\):成功对Q执行读取操作的所有事务的最大时间戳
- \(W-timestamp(Q)\):成功对Q执行写入操作的所有事务的最大时间戳
时间戳排序协议
时间戳排序协议保证对于所有冲突的\(write\)和\(read\)操作,按照时间戳顺序执行
- 假设事务\(T_i\)发出\(read(Q)\)
- 若\(TS(T_i) < W-timestamp(Q)\),\(T_i\)读入的数据项已经被(在等价的串行调度中)应该排在它后面的事务写入了,所以\(T_i\)回滚
- 若\(TS(T_i) \geq W-timestame(Q)\),\(T_i\)可以正确读入数据,正常执行\(R-timestamp(Q)\)被设置成\(TS(T_i)\)与\(R-timestamp(Q)\)的最大值
- 假设事务\(T_i\)发出\(write(Q)\)
- 若\(TS(T_i) < R-timestamp(Q)\),那么\(T_i\)要写入的数据项是被(在等价的串行调度中)应该排在它前面的事务所读取的,但前面的事务已经读取过了,所以\(T_i\)回滚
- 若\(TS(T_i) < W-timestamp(Q)\),那么\(T_i\)要写入的数据已经过时,\(T_i\)回滚
- 其他情况执行写入操作并把\(W-timestamp(Q)\)设置为\(T_i\)
事务\(T_{25}\)显示账户A和B的总余额

事务\(T_{26}\)代表B给A转账50

如下的调度假定\(TS(T_{25}) < TS(T_{26})\),并生成一个满足协议的调度
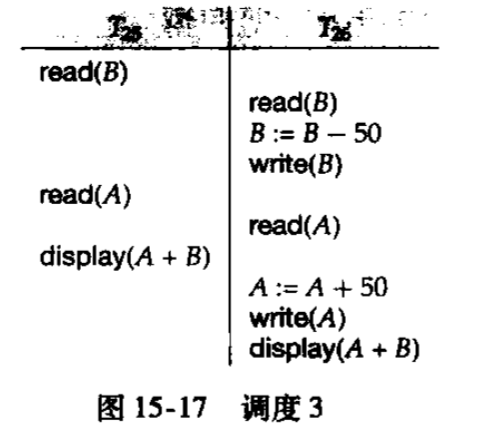
该协议天生保证冲突可串行化和无死锁。但有可能出现一个事务不断被回滚重启而出现饿死状态。
该协议也可能产生不可恢复的调度,因为该协议并未对提交做任何限制,只对写入和读出做了限制。
可以通过以下类似的办法保证可恢复:
- 对未提交数据的读取操作被推迟到更新该数据项的事务提交之后
- \(T_i\)想要提交,如果此时存在\(T_j\)写过\(T_i\)所读取的数据,那么\(T_i\)必须在\(T_j\)提交之后提交。
- 在事务末尾一次性(原子的)执行所有写操作,在此过程中,任何事务都不许访问已写完的任何数据项(没看懂???)
Thomas写规则
假定\(TS(T_{27}) < TS(T_{28})\)

如果使用刚刚的时间戳排序协议,这个\(T_{27}\)的\(read(Q)\)可以成功执行,\(T_{28}\)的\(write(Q)\)也可以成功执行,但\(T_{27}\)的\(write(Q)\)不行,因为\(TS(T_{27}) < W-timestamp(Q)\)。如果不用这套语言而用人话来说,就是这个调度不等价于一个\(T_{27}\)在\(T_{28}\)之前的串行调度。
在时间戳排序协议中,\(T_{27}\)会被回滚,但是实际上,如果想满足让两个调度等价于\(T_{27}\)在前的串行调度的话,直接忽略这个已经过时的\(T_{27}\)中的\(write(Q)\)即可,不需要回滚,这个稍微放宽限制的修改就叫Thomas写规则。
假设事务\(T_i\)发出\(write(Q)\):
- \(TS(T_i) < R-timestamp(Q)\),要写入的数据是先前需要的值,回滚
- \(TS(T_i) < W-timestamp(Q)\),要写入的数据是过时的值,忽略
- 其他,执行写入,重置\(W-timestamp(Q)\)为\(TS(T_i)\)
Thomas生成非冲突可串行化但是正确的调度。
基于有效性检查的协议
有的系统中大部分事务都是只读不写的,其实在很多系统中读操作比写操作的频率要高很多。在这种情况下我们需要一种开销更小的并发控制机制。
有效性检查协议要求事务\(T_i\)在其生命周期中按三个阶段执行
- 读阶段:读入\(T_i\)中所有数据项并保存到\(T_i\)的局部变量中,然后对于所有\(write\)操作,都针对内存中的数据进行操作
- 有效性检查阶段:对于\(T_i\)的所有\(write\)操作检测是否影响可串行性。如果有效性测试失败,中止该事务
- 写阶段:若事务已经通过有效性检查,将\(T_i\)中任何的临时局部变量复制到数据库中。只读事务没有这个阶段。
对于每个事务保存三个时间戳:
- \(Start(T_i)\):事务\(T_i\)的开始时间
- \(Validation(T_i)\):事务\(T_i\)完成读阶段并开始检测有效性的时间
- \(Finish(T_i)\):事务\(T_i\)完成写阶段的时间
我们定义\(TS(T_i) = Validation(T_i)\),通过和上面差不多的时间戳控制机制能够保证调度的可串行性。使用\(Validation(T_i)\)是因为希望在大部分事务都是只读的情况下加快响应时间(而不是使用\(Start(T_i)\))。
有效性测试要求满足\(TS(T_k) < TS(T_i)\)的事务\(T_k\)必须满足下面两个条件之一:
- \(Finish(T_k) < Start(T_i)\),\(T_k\)在\(T_i\)之前完成执行,保证了可串行性
- \(T_k\)所写的数据项集与\(T_i\)所读的数据项集不相交,且\(T_k\)的写阶段在\(T_i\)的有效性检查阶段之前完成(\(Start(T_i) < Finish(T_k) < Validation(T_i)\)。因为第一个前提条件已经指明\(T_k\)的写不影响\(T_i\)的读,并且第二个前提条件指明了\(T_i\)的写不影响\(T_k\)的读,所以可以保证可串行性次序。
没太看懂。。。
多版本机制
基于时间戳的协议的一个痛点就是,经常需要中止并重启事务,一旦有一个事务读取了已被覆盖的值时就会回滚该事务。
多版本并发控制(MVCC)机制中,\(write(Q)\)操作会创建\(Q\)的一个副本,\(read(Q)\)操作为了保证可串行性,可以挑选一个\(Q\)的副本进行读取,而不是直接宣告失败并重启。
多版本时间戳排序
多版本时间戳排序仍然使用一个\(TS(T_i)\)来记录事务\(T_i\)的时间戳,但对于数据项Q,保存一个版本序列\(<Q_1,Q_2,...,Q_m>\),每个版本包含三个数据。
- Content:该版本中数据项Q的值
- W-timestamp:创建该版本的事务的时间戳
- R-timestamp:所有成功读取该版本的事务的最大时间戳
如果事务\(T_i\)创建数据项\(Q\)的新版本\(Q_k\),\(Q_k\)的\(W-timestamp\)和\(R-timestamp\)被设置为\(T_i\),每当有一个事务\(T_j\)读取\(Q_k\)时,如果\(TS(T_j)>R-timestamp(Q_k)\),那么设置\(R-timestamp(Q_k) = TS(T_j)\)
未完...


