关系数据库设计

好的关系设计

上一篇笔记记录了由ER图直接生成关系模式的过程，生成的关系模式完全依赖ER图的质量，如果ER图质量够高，有可能直接生成还不错的关系模式。

在关系设计中，还有其它的一些设计关系模式的方法。

设计选择：更大的模式

假设我们将instructor和department两个模式组合，使用inst_dept来代替它，inst_dept模式如下

\[inst\_dept (ID, name, salary, dept\_name, building, budget) \]

显然inst_dept试图把教员和系的信息存储在一个关系模式中，这样做的好处就是我们在查询时可以使用更少的连接，通常查询效率会更高。但是这会造成很多冗余，比如多个相同系的教师，它们的系名、楼名和预算在这个设计出来的表中要重复多次，而且当我们修改时，很有可能由于疏忽造成数据不一致的问题，比如两个相同系的教师但它们的系预算budget字段不同。

很多查询频率远远大于修改更新的系统允许一部分的冗余数据，尤其是现在这个需要短时间处理大量请求的时代，但是采用这种冗余还需要注意的一点是我们没法表示一个新系，除非这个新系有了一个教师。

设计选择：更小的模式

假设现在我们设计出了inst_dept关系模式，我们可以将它们分解成原来的instructor与department关系模式的情况，并通过在instructor中保存department的主码作为外码来表示两个关系模式之间的连接。

问题是我们如何发现我们的关系模式中可以继续做这种分解，当我们的关系模式中有一个非主码，比如inst_dept中的dept_name，它能唯一确定该关系模式中的另几个值，比如dept_name能够唯一确定budget(只要inst_dept中的任意两个元组的dept_name属性相同，那么它们的budget属性一定也相同)，那么dept_name能够单独拿出来作为它能唯一确定的那些属性的主码。

一个关系模式中的一个属性能确定另外的属性，这个现象就叫函数依赖(functional dependency)，用dept_name和budget举例，就是如果存在模式(dept_name, budget)，则dept_name可以作为单独的主码，记作：

\[dept\_name \to budget \]

原子域和第一范式

范式(normal form)，你一看英文名就明白了，就是给出我们定义关系模式的一般形式，我们可以遵循这些形式去定义关系模式。

在说范式之前，先说，范式是一些好的关系设计模式，但也不完全绝对，现在为了获得更高的查询效率而做反范式设计很常见。

原子域就是我们的域不可再分，ER模型中允许多值属性和组合属性，而这些属性都不叫原子域。如果一个关系模式R的所有属性都是原子的，那么关系模式R符合第一范式(1NF)。

一个例子：

假设一个机构给雇员的编号形如所在岗位+编号的形式，比如CS1101、EE2018那么这个编号就不是原子的。

非原子域带来的坏处就是雇员所在岗位需要应用层自行设计算法通过编号来解析，而且一个雇员如果更换岗位了，那么它的编号还有所有引用到它编号的位置都要更改。

但如果该数据库系统只是这样编码编号，并没有单纯通过编号来表示岗位，而是通过一个其它的字段，比如sec_id来表示员工所在岗位，那么这也不算非原子域。

所以是否是非原子域只看数据库系统有没有依赖一个属性来表示多个值。

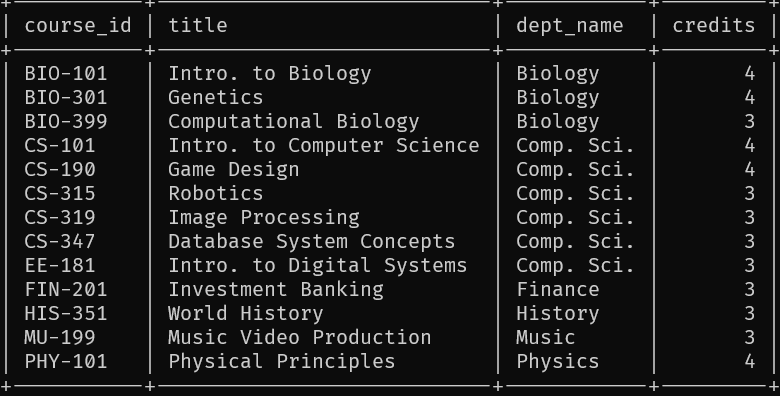
我们的大学数据库系统中虽然采用CS-101这种字符串为课程编号，但它仍保留了表示所在系的属性dept_name，所以我们的大学关系模式设计符合第一范式。

使用函数依赖进行分解

符号

• \(R\)代表一个关系的属性集
• \(r(R)\)代表关系\(r\)的关系模式，\(R\)是\(r\)的全部属性，当我们不关心关系的名字时，也会只用\(R\)代表一个关系。
• \(K\)表示超码，经常看到\(K\)是\(r(R)\)的超码这种表述

用这些符号重新说明超码的概念

如果\(R\)的子集\(K\)是\(r(R)\)的超码，那么对于\(r\)中的任意两个元组\(t_1\neq t_2\)，都满足\(t_1[K] \neq t_2[K]\)

就是说在一个关系中不可能存在两个元组在属性集K上完全相同，称K为\(r(R)\)的超码。

函数依赖

我们再用上面的符号重新说明函数依赖

函数依赖能够确定一个关系中一些属性对另一些属性的约束，比如一个系(dept_name)只能有一个预算值(budget)

考虑\(r(R)，\alpha \subseteq R, \beta \subseteq R\)

1. \(\alpha \to \beta\)的条件是：对于\(r(R)\)的关系实例中的所有元组对\(t_1,t_2\)，若\(t_1[\alpha] = t_2[\alpha]\)，则\(t_1[\beta] = t_2[\beta]\)
2. 如果\(r(R)\)中的每个合法实例都满足函数依赖\(\alpha \to \beta\)，那么称该函数依赖在\(r(R)\)上成立(hold)

使用函数依赖来表达超码的概念，则是：若函数依赖\(K\to R\)在\(r(R)\)上成立，那么\(K\)是\(r(R)\)的超码。

一个函数依赖是平凡的，因为它们在所有关系中都满足，比如\(\alpha \to \alpha\)在所有具有属性\(\alpha\)的关系中都满足，再比如\(\alpha\beta \to \alpha\)。一般地说，\(A\to B\)是平凡的，如果\(B\subseteq A\)。

需要注意到的是，在现实情况中，一个关系实例可能满足函数依赖，但在关系模式的定义上不满足。

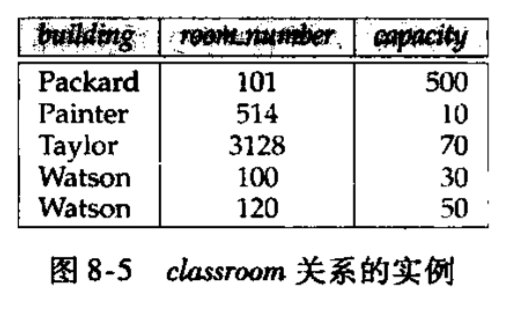
比如下图，\(room\_number \to capacity\)没什么问题，但是现实情况是可能不在同一个建筑的房间，它们有相同的房间号，但它们能容纳的人数不同，所以\(room\_number \to capacity\)不一定成立，而\(building, room\_number \to capacity\)则成立。

如果有\(r(A,B,C)\)，\(A\to B\)在\(r\)上成立，\(B\to C\)在\(r\)上成立，那么\(A\to C\)在\(r\)上也一定成立，因为\(A\)唯一约束\(B\)，\(B\)唯一约束\(C\)，所以\(A\)也能够唯一约束\(C\)。

Boyce-Codd 范式

Boyce-Codd范式(BCNF)能够消除所有基于函数依赖能够发现的冗余。

BCNF规定，具有函数依赖集\(F\)的关系模式\(R\)，对\(F\)中所有的函数依赖\(\alpha \to \beta\)， \(\alpha, \beta\)都包含于\(R\)，那么下面至少有一项成立：

1. \(\alpha \to \beta\)是平凡函数依赖
2. \(\alpha\)是模式\(R\)的一个超码

一个数据库设计符合BCNF的条件是构成该设计的关系模式集中的每一个模式都属于BCNF。

比如如下关系模式不属于BCNF范式

\[inst\_dept (ID, name, salary, dept\_name, building, budget) \]

因为\(dept\_name \to budget\)在\(inst\_dept\)上成立且\(dept\_name\)不是超码。

将一个不属于BCNF范式的关系模式分解称属于BCNF的关系模式分为两步。

假设\(R\)是不属于BCNF的一个模式，则至少存在一个非平凡函数依赖\(\alpha \to \beta\)且\(\alpha\)不是R的超码，那么我们可以将R分解成如下两个模式：

1. \((\alpha \cup \beta)\)
2. \((R-(\beta - \alpha))\)

比如\(inst\_dept\)的例子，\(\alpha=\left \{ dept\_name \right \}\)，\(\beta = \left \{building, budget\right \}\)

1. \((\alpha \cup \beta) = (dept\_name, building, budget)\)
2. \((R-(\beta - \alpha)) = (ID, name, dept\_name, salary)\)

在该例子中，\(\beta - \alpha\)的作用没有体现，当一个函数依赖两面出现相同的属性时这个就有作用了，可以尝试自己构造一个。

分解后的模式可能产生一个或多个不属于BCNF范式的模式，应继续分解。

保持依赖

在BCNF范式下，如果系统的需求更改，那么函数依赖可能得不到保持。

比如一个学生可以有多位导师，但在指定的系只能有一位，可以用如下符合BCNF的关系模式表示

\[dept\_advisor (s\_ID, i\_ID, dept\_name) \]

上面的关系模式中\(s\_ID, i\_ID \to dept\_name\)

如果现在我们有了附加约束，一位教师只能在一个系担任导师，那么上面的关系模式就不符合BCNF了，因为

\[i\_ID \to dept\_name \\ s\_ID, dept\_name \to i\_ID \]

函数依赖左边的都不是平凡依赖且它们都不是超码，所以要对dept_advisor进行分解，根据BCNF分解规则，得到如下两个关系

\[(s\_ID, i\_ID)\\ (i\_ID, dept\_name) \]

这种修改了需求就需要重新计算函数依赖并更新关系模式的设计称为不是保持依赖(dependency preserving)的，我们需要一种比BCNF更弱的范式来保持依赖，这个范式就是第三范式(3NF)。

第三范式

第三范式(third normal form, 3NF)规定，具有函数依赖集\(F\)的关系模式\(R\)，对\(F\)中所有的函数依赖\(\alpha \to \beta\)， \(\alpha, \beta\)都包含于\(R\)，那么下面至少有一项成立：

1. \(\alpha \to \beta\)是平凡函数依赖
2. \(\alpha\)是模式\(R\)的一个超码
3. \(\beta - \alpha\)中的每个属性A都包含于R的一个候选码中

候选码即最小的超码，候选码是任何真子集都不是超码的超码。

第三范式通过附加的条件3放款了BCNF的限制，任何符合BCNF的设计都符合3NF。

还是上面的例子。

\[i\_ID \to dept\_name \\ s\_ID, dept\_name \to i\_ID \]

这时显然对于第三范式的前两条约束，也就是BCNF的约束都不满足，但是\(dept\_name - i\_ID = dept\_name\)，而\(s\_ID, dept\_name\)又构成了\(dept\_advisor\)的一个候选码，所以满足3NF的第三条约束。

更高的范式

BCNF和3NF使用函数依赖来进行关系模式的分解，在开篇也说了，函数依赖只能处理部分冗余，也就是说符合BCNF和3NF的关系模式设计可能仍有一部分冗余。

比如instructor关系现在要记录教师的孩子和电话号，这两个都是多值属性，因为教师可能有多个孩子和多个电话号，通过ER图转换为关系模式后就会分解成这样两个关系模式

\[(ID, child)\\ (ID, phone\_number) \]

如果把这两个关系合并，仍然符合BCNF和3NF，因为这个关系中都是平凡的函数依赖，没有一个属性能唯一确定另一个属性

\[(ID, child, phone\_number) \]

考虑一个教师有两个孩子和两个电话，我们不得不将所有的排列组合列出才能表示完整的信息

\[(99999, David, 512-555-1234)\\ (99999, David, 512-555-4567)\\ (99999, William, 512-555-1234)\\ (99999, William, 512-555-4567) \]

更高的范式用于处理这种冗余，后面介绍。

函数依赖理论

三条公理

这三条公理称作Armstrong公理

• 自反率(reflexivity rule)：\(\beta \subseteq \alpha , \alpha \to \beta\)
• 增补率(augmentation rule)：\(\alpha \to \beta, \alpha \gamma \to \beta \gamma\)
• 传递率(transitivity rule)：\(\alpha \to \beta, \beta \to \gamma, \alpha\to\gamma\)

推演

推演部分推荐各位自行ss演

合并率(union rule)

若\(\alpha \to \beta, \alpha \to \gamma\)证明\(\alpha \to \beta \gamma\)

\[\because \alpha \alpha \to \alpha \beta(增补率) ,\alpha = \alpha \alpha\\ \therefore \alpha \to \alpha \beta \\ \because \alpha \to \gamma\\ \therefore \alpha \beta \to \beta \gamma (增补率)\\ \because \alpha \to \alpha\beta , \alpha \beta \to \beta \gamma\\ \therefore \alpha \to \beta\gamma \]

对于\(\alpha=\alpha \alpha\)可能需要说明一下，因为函数依赖操作的都是属性集，所以当我们写\(\alpha \alpha\)时，实际上是取两个属性集的并集，也就是\(\alpha \cup \alpha\)，那么自然就剩下\(\alpha\)了，所以\(\alpha = \alpha \alpha\)

分解率(decomposition)

若\(\alpha \to \beta \gamma\)成立，则\(\alpha \to \beta\)和\(\alpha \to \gamma\)成立

\[\because \alpha \to \beta\gamma, \beta \gamma \to \beta(自反率)\\ \therefore \alpha \to \beta(传递率)\\ 同样\\ \because \alpha \to \beta\gamma,\beta\gamma \to \gamma\\ \therefore \alpha \to \gamma \]

伪传递率(pseudotransitivity rule)

若\(\alpha \to \beta\)和\(\gamma \beta \to \delta\)成立，则\(\alpha \gamma \to \delta\)成立

\[\because \alpha \to \beta \therefore \alpha \gamma \to \gamma \beta (自反率)\\ \because \gamma \beta \to \delta \therefore \alpha\gamma \to \delta (传递率) \]

例子

\(r(A,B,C,G,H,I)\)以及函数依赖集\(F\)

\[A \to B\\ A \to C\\ CG \to H\\ CG \to I\\ B \to H \]

给定一个函数依赖集\(F\)，被\(F\)蕴含的所有函数依赖集合称为\(F\)的闭包，记作\(F^+\)，上面一些公理和我们推演出来的定律可以用来计算\(F^+\)。

比如，\(A\to H\)可以推出，因为\(A\to B, B\to H\)。是传递率。

再比如\(CG\to HI\)可以推出，因为\(CG \to H, CG \to I\)。是合并率。

再比如\(AG\to I\)可以推出，因为\(A \to C, CG \to I\)。是伪传递率。

可以设计出一个算法来找出给定函数依赖集的闭包\(F^+\)，并且可以通过这个来设计出BCNF分分解算法和3NF分解算法，能力有限不研究了，可以去看原书。

多值依赖

回头看这个例子

\[(ID, child, phone\_number) \]

这个关系模式可能有如下实例

\[(99999, David, 512-555-1234)\\ (99999, William, 512-555-4567)\\ (99999, David, 512-555-4567)\\ (99999, William, 512-555-1234)\\ \]

这个实例代表一个教师有多个孩子和多个电话号，我们要把所有排列组合写上才能完整表示信息，这是一个冗余，这种冗余就叫多值依赖。它的一般定义如下

另\(r(R)\)为一个关系模式，\(\alpha \subseteq R\)且\(\beta \subseteq R\)，如果对于r中任一满足\(t_1[\alpha]=t_2[\alpha]\)的元组对\(t_1\)和\(t_2\)，r中都存在元组\(t_3\)和\(t_4\)使得：

\[t_1[\alpha] = t_2[\alpha] = t_3[\alpha] = t_4[\alpha]\\ t_3[\beta] = t_1[\beta]\\ t_3[R-\beta] = t_2[R-\beta]\\ t_4[\beta] = t_2[\beta]\\ t_4[R-\beta] = t_1[R-\beta]\\ \]

那么称\(r(R)\)上有多值依赖\(\alpha \to \to \beta\)

如果你注意到我把上面的例子调换了顺序，那么你可以把这个复杂的定义套到上面的示例中取对比一下应该就明白了，\(\alpha\)是教师ID，\(\beta\)是孩子姓名，多值依赖说的就是上面的情况。

多值依赖所讲述的就是\(\alpha\)和\(\beta\)之间的联系独立于\(\alpha\)和\(R-\beta\)之间的联系，在上面的例子中就是教师ID与孩子姓名的联系独立于教师ID与教师电话号之间的联系。说白了就是同一个表中存在多对多关系，即，在上面的例子中，同一个表中的多个孩子对应着多个父母的电话。

如果\(\beta \subseteq \alpha\)或者\(\beta \cup \alpha=R\)，则\(\alpha \to \to \beta\)是平凡的。这限定了多值依赖的两个属性必须是各自独立的，它们可以有交集但不能完全是包含关系，而且它们的并集不能是关系中的所有属性。

• 若\(\alpha \to \beta\)，那么\(\alpha \to \to \beta\)
• 若\(\alpha \to \to \beta\)，则\(\alpha \to \to R-\alpha -\beta\)

第四范式

对于函数依赖集和多值依赖集为D的关系模式\(r(R)\)，属于第四范式(4NF)，如果\(D^+\)中所有形如\(\alpha\to \to \beta\)的多值依赖(\(\alpha \subseteq R, \beta \subseteq R\))，至少有以下之一成立：

• \(\alpha \to \to \beta\)是一个平凡多值依赖
• \(\alpha\)是\(R\)的一个超码

4NF一定属于BCNF，因为一个\(r(R)\)不属于BCNF，那么他一定存在一个非平凡函数依赖\(\alpha \to \beta\)，且\(\alpha\)不是超码，因为\(\alpha \to \beta\)就意味着\(\alpha \to \to \beta\)，所以\(r(R)\)不属于4NF。