关系代数
基本运算
选择运算
选择选出关系中满足给定谓词的元组，组成新的关系，用小写希腊字母sigma(\(\sigma\))来表示选择，谓词写作\(\sigma\)的下标，关系则作为参数在括号中出现。
选择instructor关系中物理系的那些元组。
\[\sigma_{dept\_name="Physics"}(instructor)
\]
比较运算符包括\(=,\neq, \lt, \leq, \gt, \geq\)。
逻辑运算包括\(\wedge(and), \vee(or), \neg(not)\)
下面找到物理系并且工资大于90000的教师。
\[\sigma_{dept\_name="Physics" \wedge salary > 90000}(instructor)
\]
选择谓词中也可以包括两个属性的比较，下面选出系名和楼名相同的系
\[\sigma_{dept\_name=building}(department)
\]
投影运算
当只需要关系中的部分属性时可以使用投影运算，用大写字母\(\Pi(pi)\)来表示
下面选择instructor中的ID、dept_name和salary字段。
\[\Pi_{name, dept\_name, salary}(instructor)
\]
关系运算的组合
由于之前我们学的两个运算都需要一个关系并返回一个关系，所以可以把它们组合起来。
\[\Pi_{name}(\sigma_{dept\_name="Physics"}(instructor))
\]
并运算
查询2009年秋和2010年春开课的所有课程的集合
2009年秋
\[\sigma_{semester="Fall" \wedge year=2009}(section)
\]
2010年春
\[\sigma_{semester="Spring" \wedge year=2010}(section)
\]
并集
\[\sigma_{semester="Fall" \wedge year=2009}(section) \cup \sigma_{semester="Spring" \wedge year=2010}(section)
\]
注意，我们不用像SQL一样进行手动去重，因为关系本身在数学中的定义就是集合，不会有重复数据。
对于并集运算\(r\cup s\)，需要满足
- 关系r和s必须同元，即它们的属性数目必须相同
- 它们对于r的第i个属性\(r_i\)，s的第i个属性\(s_i\)的域和\(r_i\)的域一致
集合差运算
在2009年秋季开课但并不在2010年春季开课的课程
\[\sigma_{semester="Fall" \wedge year=2009}(section) - \sigma_{semester="Spring" \wedge year=2010}(section)
\]
笛卡尔积运算
\[r \times s
\]
查找物理系教师并显示出它们教授的课程
\[\sigma_{instructor.ID=teaches.ID}(\sigma_{dept\_name="Physics"}(instructor \times teaches))
\]
更名运算
\[\rho_x(r)
\]
将关系r重命名为x。
\[\rho_{x(A_1,A_2,...,A_n)}(r)
\]
将关系r重命名为x，并将其中的属性重命名为\(A_1...A_n\)
也可以使用\(\$i\)的方式访问第\(i\)个属性，而不用重命名属性。
附加关系代数运算
上面的基本运算在很多时候会显得冗长，所以要设计一些附加的符号来进行运算。
集合交运算
\[r\cap s
\]
返回r和s的交集。每一个集合交运算可以通过\(r=r-(r-s)\)来得到。
自然连接
\[r\Join s
\]
表示r与s进行自然连接。
外连接
左外
\[r \sqsupset \Join s
\]
右外
\[r \Join \sqsubset s
\]
全外
\[r \sqsupset \Join \sqsubset s
\]
广义投影
就是可以在投影的属性里进行算术运算
\[\Pi_{F_1, F_2, ... ,F_n}(E)
\]
E是关系表达式，F1到Fn是E中属性的算术表达式
聚集函数
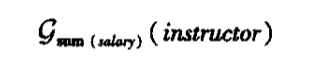
这个我不会打。。。
元组演算
略
域关系盐酸
略
