紫书第八章竞赛题目
抄书（Copying Books, UVa 714）
输入输出
第一行代表有n组数据，以下n组数据每组两行，第一行是m和k，第二行的m个数是序列。
对于每组输入，输出最优的划分方式。
Sample Input
2
9 3
100 200 300 400 500 600 700 800 900
5 4
100 100 100 100 100
Sample Output
100 200 300 400 500 / 600 700 / 800 900
100 / 100 / 100 / 100 100
思路
此题没法暴力破解，如果仅从这个序列上思考，很难思考出个可行的，在规定时间范围内能完成的解决方法。
紫书中是这样想的。
设定谓词\(P(x)\)代表的含义为，是否能在每组子序列的和都不超过x的前提下将原序列划分成k个子序列。若能分成，这个x可能就是答案中最大的\(S(i)\)或者比\(S(i)\)还大，那就使用二分查找搜索左边，如果不能分成，就证明答案中最大的\(S(i)\)一定比x大，使用二分查找搜索右边。
而\(P(x)\)的执行只需要一次遍历，时间复杂度是\(O(n)\)，外层的二分查找是\(O(log_2n)\)，那么总的复杂度就是\(O(nlog_2n)\)。
我试着对\(P(x)\)的时间复杂度来优化，可以经过一次预处理将序列的后n项和算出来，然后因为序列中都是正整数，这个后n项和肯定是递增的，所以这里也能够使用二分查找。但写着写着就写乱了，所以效果不是特别好，代码将就着看吧，看不懂的话不怪你，怪我写的太乱了。。我尽量多写些注释。
代码
#include "iostream"
#include "cstdio"
#include <algorithm>
#include <queue>
#include "cmath"
using namespace std;
#define MAX 500
#define Num long long
// 输入序列
int seq[MAX];
/*
后n项和序列
假设输入序列是 2 3 1 4 5
后n项和序列则是 15 13 10 9 5
*/
Num S[MAX];
int m, k,max_n=0;
// deque用于暂存P(x)中选择的分割线插入位置，min_ans代表当前找到的最小x的分割线插入位置
deque<int> pos,min_ans;
bool cmp_desc(Num a, Num b) {
return a > b;
}
bool P(Num x) {
pos.clear();
Num find = x,*it;
// 尝试在每组数和<=x的情况下分割成k组
for (int i = 0; i < k; i++) {
// 如果只剩下最后一组数，那么只需要判断最后一组加起来是不是<=x，是的话就能分割
if (i == k - 1) {
if (S[0] - (*it) <= x)return true;
}
else {
// 如果不是最后一组数，那么每次都在后n项和序列中找到我们当前要寻找的数，如果没有此数，返回比它要大的第一个，这个数就是分割的位置
it = lower_bound(S, S + m, find,cmp_desc);
// 如果找到头了，结束查找 其实这里逻辑有问题，因为第一个有可能直接大于x，不过不影响算法的正确性，这是我提交后才想到的
if (it == S)return true;
// 插入分割位置
pos.push_front(it - S -1);
// 迭代find
find = x + (*it);
}
}
return false;
}
void showAns() {
int j = 0;
for (int i = 0; i < m; i++) {
cout << seq[i];
if (i != m - 1)cout << " ";
if (j<min_ans.size() && min_ans[j] == i) { cout << "/ "; j++; }
}
cout << endl;
}
int main() {
int kases;
scanf("%d", &kases);
for (int c = 0; c < kases; c++) {
max_n = 0; min_ans.clear(); pos.clear();
scanf("%d %d", &m, &k);
for (int i = 0; i < m; i++) {
scanf("%d", &seq[i]);
}
// 如果k为1，不用分割
if (k == 1) {
showAns(); continue;
}
// 计算后n项和
for (int i = m - 1; i >= 0; i--) {
if (i == m-1)S[i] = seq[i];
else S[i] = seq[i] + S[i + 1];
max_n = max(max_n, seq[i]);
}
// 初始化左边界和右边界，开始二分查找
// 对于P(x)，x不可能比整个序列中的最大值还要小
// 也不可能比整个序列的和还要大
Num l = max_n, r = S[0],min_mid=r;
while (l < r) {
Num mid = (l + r) / 2;
if (P(mid)) {
if (mid < min_mid) {
min_mid = mid;
// 因为P函数中只是对能不能划分做了一个测试，有的时候返回的pos是缺少或不准确的，所以如果pos不准确，就重新计算。
if (pos.size() == k - 1) {
min_ans = pos;
}
else {
// 重新计算答案
min_ans = deque<int>();
int s=0;
for (int i = m-1; i >= 0; i--) {
s += seq[i];
// 因为mid传入了P谓词，所以mid就是上面所说的x。
// 若当前加和已经大于x了，或者前面的数字个数最多只能再分出剩下的组数时
// 插入分割线
if (s>mid || k - min_ans.size() == i+2) {
min_ans.push_front(i);
s = seq[i];
}else if(s==mid){
// 若当前加和等于x，在前面插入分割线
min_ans.push_front(i-1);
s = 0;
}
// 分组完毕，分割线数==组数-1
if (min_ans.size() == k - 1) { break; }
}
}
}
r = mid;
}
else {
l = mid + 1;
}
}
showAns();
}
return 0;
}
全部相加（Add All, UVa 10954）
有n（n≤5000）个数的集合S，每次可以从S中删除两个数，然后把它们的和放回集合， 直到剩下一个数。每次操作的开销等于删除的两个数之和，求最小总开销。所有数均小于\(10^5\)。
输入输出
每组数据包含两行，第一行是一个整数n，第二行的n个数是输入序列。
对于每组输入，输出把他们全部相加的最小开销。
Sample Input
3
1 2 3
4
1 2 3 4
0
Sample Output
9
19
思路
这就是Huffman编码树，每次选择两个最小的，相加，并且把结果放到集合中。
关于算法的正确性，这是一个贪心算法，因为想要总开销最小，并且相加的结果还要放回集合中，那么很自然的就能想到每次选择两个最小的数相加。
诶试试用反证法？
假设\(a\)和\(b\)是当前集合中最小的，它们相加之后，总开销增加了\(a+b\)，现在假设这个开销并不是当前阶段的最小开销，那么必然存在其他的一对数，比如\(c\)和\(d\)，并且\(c+d<a+b\)，可是\(a\)和\(b\)是当前集合中最小的，不可能大于\(c+d\)，所以这个开销就是当前阶段的最小开销。
代码
#include "iostream"
#include "cstdio"
#include "queue"
using namespace std;
int main() {
int n;
priority_queue<int,vector<int>,greater<int> > q;
while (scanf("%d", &n) != EOF,n) {
while(!q.empty())q.pop();
for (int i = 0; i < n; i++) {
int t; scanf("%d", &t);
q.push(t);
}
int ans = 0;
while (q.size() > 1) {
int a = q.top(); q.pop();
int b = q.top(); q.pop();
ans += a + b;
q.push(a + b);
}
printf("%d\n", ans);
}
return 0;
}
奇怪的气球膨胀（Erratic Expansion, UVa12627）
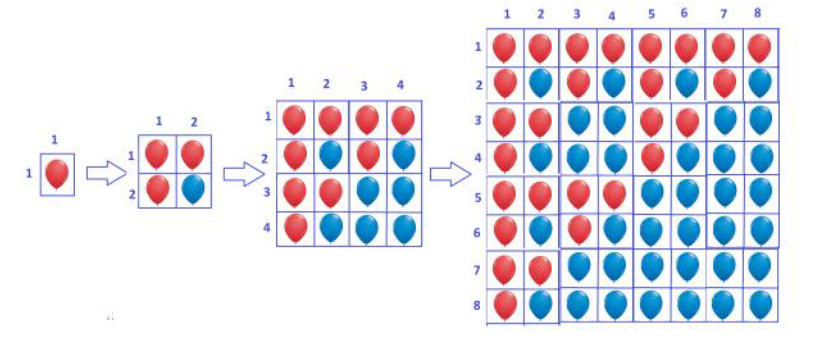
一开始有一个红气球，每经过一个小时，一个红气球分裂成三个红气球，一个蓝气球。就像下图。
给你三个数，A,B,K，求经过K小时，[A,B]之间的红气球数量。
输入输出
第一行是一个数T，不超过1000，代表示例总数，以下的T行每行是一个示例，包含三个数，分别是K，A和B，K在[0,30]中。
对于每组示例，输出经过K小时，[A,B]之间的红色气球数量。
Sample Input
3
0 1 1
3 1 8
3 3 7
Sample Output
Case 1: 1
Case 2: 27
Case 3: 14
思路
想了三个版本的递推。
第一个版本是\(cnt(r,K)\)代表K小时后，r行的红气球数，则答案为。
那么cnt函数如何计算？通过观察发现，每隔一小时不过是把当前的图案作为下一次图案的左上角，并复制了两份，作为左下和右上，而右下角全是蓝色。那么，对于\(cnt(r,K)\)，如果r在图形的下半部分\((r>2^{k-1})\)，那么其中的红色气球数为$cnt(r-\(2^{k-1}\),k-1)$，就是当k-1小时时对应的上半部分的行的红色气球数量，因为是从那里复制过来的，所以没问题。对于r在上半部分就更简单了，可以变成\(2\times cnt(r,k-1)\)。
我们应该给这个递推式一个基本解，就是当\(k=0,r=1\)时，有1个红色气球。
这不是一个好的递推算法，需要\(k\times (B-A)\)次循环。是\(O(n^2)\)的复杂度。
第二个版本的递推，是按区域来递推，省去了一层循环，但由于A和B的差异可能很大(最大可差\(2^{30}-1\))，所以这个线性时间的复杂度也难以应付题目中1000毫秒的要求，这里不写了。
第三个版本是紫书的版本，利用了一个我之前从没注意到的点。
\(c(k)\)是k小时后总共的红气球数，不难发现\(c(k) = 3^k\)，因为每次复制三个原来的图形。
\(f(K,B)\)是k小时后前B行的红气球数，那么\(f(K,B) - f(K,A-1)\)就是所求的区间内红气球的数量。
现在只需要找到\(f(K,B)\)的递推关系就好了。
还是分成两部分，当B在上半部分时\((B<=2^{k-1})\)，红气球的数量为\(2\times f(K-1,B)\)，因为左右两边是一样的，只需要递推求解一个乘二即可，当在下半部分时，则为\(2\times c(K-1) + f(K-1,B-2^{k-1})\)，加法中前面一项是上面一半所有的红气球数，因为都占满了，所以直接用c函数就可以计算，省去了很多递推的麻烦。
规定当\(f(0,1)=1\)，\(f(K,r)(K<0||B<=0) = 0\)。
时间复杂度\(O(K)\)，虽然也是线性，但K的取值范围是[0,30]，大大降低运行时间。
代码
#include "iostream"
#include "cstdio"
#include "cmath"
using namespace std;
#define LL long long
LL c(int k) {
return pow(3, k);
}
LL f(int K, int B) {
if (K == 0 && B == 1)return 1;
if (K <= 0 || B <= 0)return 0;
int km1pwr = 1 << (K - 1);
if (B < km1pwr)return 2 * f(K - 1, B);
return 2 * c(K - 1) + f(K - 1, B - km1pwr);
}
int main() {
int T, K, A, B;
scanf("%d", &T);
for (int i = 1; i <= T; i++) {
scanf("%d %d %d", &K, &A, &B);
printf("Case %d: %lld\n",i,f(K,B) - f(K,A-1));
}
return 0;
}
