紫书第八章例题笔记
煎饼（Stacks of Flapjacks, UVa120）
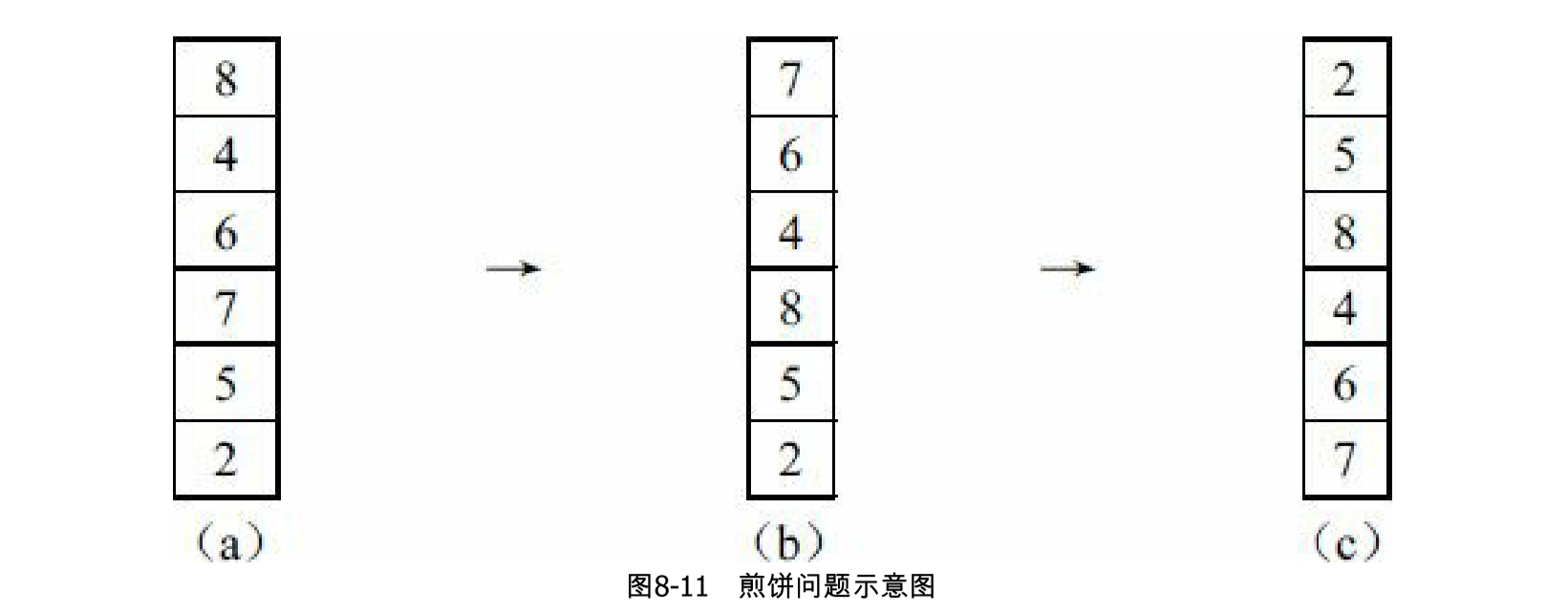
有一叠煎饼正在锅里。煎饼共有\(n（n≤30）\)张，每张都有一个数字，代表它的直径大小，如图8-11所示。flip(k)操作可以把铲子插到倒数第k张煎饼下面，并且翻转铲子上面所有的煎饼。例如，图8-11（a），依次执行操作flip(3),flip(1)后得到图8-11（c）的情况。
设计一种方法使得所有煎饼按照从小到大排序（最上面的煎饼最小）。输入时，各个煎饼按照从上到下的顺序给出。例如，上面的例子输入为8, 4, 6, 7, 5, 2。
输入输出
输入包含多行，每行是一组以空格分开的数字，这些是煎饼的直径。直径不会超过100，每组数不会超过30。输入代表初始时这些煎饼的序列。
对于每组输入，输出原序列和flip操作的参数，每组输出以0结束。
Sample Input
1 2 3 4 5
5 4 3 2 1
5 1 2 3 4
Sample Output
1 2 3 4 5
0
5 4 3 2 1
1 0
5 1 2 3 4
1 2 0
思路
看到题目都傻了，没啥规律可循，题目中没说明要求输出的内容中flip次数最少还是咋样，就给你几个输入输出让你做。
紫书中的思路是，假设有n个煎饼，每次在[1~n]范围找直径最大的煎饼，如果它在位置k，先用flip(k)把它放到顶上，再用flip(1)让它到底部。这时这个直径最大的煎饼已经归到正确的位置了，我们缩小范围至[1~n-1]，重复上面步骤。
这样确实能得到正确结果，思路也很巧妙，但是我还是不知道也不给一个输出的详细要求就让我做怎么做啊，会不会存在其他flip参数序列也能将煎饼排序？？？
代码
刚开始没想太多直接开始编码了，导致写的乱七八糟，心里在想很多时间优化策略，但是就这问题的输入规模，\(O(n^3)\)的时间复杂度也无所谓吧。所以应该追求简洁易懂。
#include "iostream"
#include "cstdio"
#include "string"
#include "sstream"
#include <algorithm>
#include "cmath"
#include "cstring"
using namespace std;
string line;
int stack[31]; // stack[i] 当前栈中第i张饼的直径 从1开始
int position[101]; // position[n] 饼面直径为n的元素所在栈中的位置，因为并无相同直径的饼 从1开始
int n,maxi = 0;
void read() {
memset(position, -1, sizeof(position));
stringstream ss(line);
n = 1;
while (ss >> stack[n]) { position[stack[n]] = n;maxi = max(stack[n++],maxi); }
n--;
for (int i = 1; i <= n; i++)
printf("%d%c", stack[i], i == n ? '\n': ' ');
}
void swap(int* p, int* q) {
int t = *p; *p = *q; *q = t;
}
// 从倒数第pos个开始，将i到上面的所有翻转
void flip(int pos){
if (pos == n)return;
cout << pos << " ";
for (int i = n - pos + 1, j = 1; i > j; i--, j++) {
position[stack[i]] = j; position[stack[j]] = i;
swap(stack + i, stack + j);
}
}
void solve(){
int correctCnt = 0; // 已经在正确位置的饼的数量
for (int i = maxi; i >= 0 && correctCnt <= n; i--) {
if (position[i] != -1) {
// 位置不正确，翻转
if(position[i] != n-correctCnt){
flip(n-position[i]+1); flip(correctCnt+1);
}
correctCnt++;
}
}
}
int main() {
while (getline(cin,line)) {
read();
solve();
printf("0\n");
}
return 0;
}
联合国大楼（Building for UN, ACM/ICPC NEERC 2007, UVa1605）
你的任务是设计一个包含若干层的联合国大楼，其中每层都是一个等大的网格。有若干国家需要在联合国大楼里办公，你需要把每个格子分配给一个国家，使得任意两个不同的国 家都有一对相邻的格子（要么是同层中有公共边的格子，要么是相邻层的同一个格子）。你设计的大厦最多不能超过1000000个格子。
输入国家的个数n（n≤50），输出大楼的层数H、每层楼的行数W和列数L，然后是每层楼的平面图。不同国家用不同的大小写字母表示。
输入输出
Sample Input
4
Sample Output
2 2 2
AB
CC
zz
zz
思路
明白了，这种题的判定并不是死的，因为实现方法不只有一个，提交后OJ会测定你的输出是否满足要求。
这题的思路很简单，因为也没要求使用的网格数最少，所以用两层\(n\times n\)的网格解决，第一层每一行都是一个国家，第二行每一列都是一个国家即可。
之前把思想禁锢在单个国家，没想到这种办法。
代码
#include "iostream"
#include "cstdio"
#define MAX 51
using namespace std;
char chs[MAX] = "ABCDEFGHIJKLMNOPQRSTUVWXYabcdefghijklmnopqrstuvwxy";
int main() {
int n,h,w,l;
while (scanf("%d", &n) != EOF) {
printf("2 %d %d\n", n, n);
for (int l = 0; l < 2; l++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
printf("%c", l == 0 ? chs[i] : chs[j]);
printf("\n");
}
printf("\n");
}
}
return 0;
}
和为0的4个值（4 Values Whose Sum is Zero, ACM/ICPC SWERC 2005, UVa 1152）
给定4个n（1≤n≤4000）元素集合A, B, C, D，要求分别从中选取一个元素a, b, c, d，使得 a+b+c+d=0。问：有多少种选法？ 例如，A={-45,-41,-36,26,-32}, B={22,-27,53,30,-38,-54}, C={42,56,-37,-75,-10,-6}, D={-16,30,77,-46,62,45}，则有5种选法：(-45, -27, 42, 30), (26, 30, -10, -46), (-32, 22, 56, -46),(-32,30, -75, 77), (-32, -54, 56, 30)。
输入输出
输入第一行是示例数，每组示例第一行是n，即四组数的长度。
对于每组示例，输出四组数中任选一个，相加为0的组数。
Sample Input
1
6
-45 22 42 -16
-41 -27 56 30
-36 53 -37 77
-36 30 -75 -46
26 -38 -10 62
-32 -54 -6 45
Sample Output
5
思路
四重枚举肯定不行，\(O(n^4)\)的复杂度，而n最大是4000。太大了。
第七章的经验，可以想到，只需要关心前三组数就行了，计算出前三组数所有的加法组合，放到map中，再线性扫描一次第四组即可算出为0的组合数，这样一来复杂度变为\(O(n^3log_2n)\)，后面的对数来自于map的查找复杂度，当然使用其他数据结构则有不同的复杂度。对于n是4000，还是太大。
最终紫书中给出的解决办法是，线性扫描前两组，算出所有加法组合，放到map中，然后再扫描后两组，算出所有加法组合，和map中的比较。这样的复杂度是\(O(n^2log_2n)\)，凑凑合合能应付。
代码
使用map TLE了，看下面题解使用的vector和二分查找，如果map的实现是TreeMap，两种方法复杂度并无差别，不知为何TLE。
改成vector的了，然后现在UVA挂了，还没提交，先贴代码。别管A不AC了。
当日晚上更新
UVA好了，提交了，之前的代码PE了，改动在下面用注释标注了出来
#include "iostream"
#include "cstdio"
#include "vector"
#include <algorithm>
using namespace std;
int nums[4][4000];
vector<int> cacheForAB;
int main() {
int kases;
scanf("%d", &kases);
int n,ans;
for (int i = 0; i < kases; i++) {
if (i > 0)printf("\n"); // [+] 添加此行
scanf("%d", &n);
cacheForAB.clear();
ans = 0;
// 输入
for (int j = 0; j < n; j++)for (int k = 0; k < 4; k++) scanf("%d", &nums[k][j]);
// 计算AB相加得到的所有结果，放入缓存
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
cacheForAB.push_back(-(nums[0][i] + nums[1][j]));
// 计算CD相加得到的所有结果，判断缓存中有没有，有就代表和ab能产出的所有结果中的一个相加为0
sort(cacheForAB.begin(), cacheForAB.end());
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++) {
vector<int>::iterator s, e;
s = lower_bound(cacheForAB.begin(), cacheForAB.end(),nums[2][i]+nums[3][j]);
if (s == cacheForAB.end())continue;
e = upper_bound(cacheForAB.begin(), cacheForAB.end(), nums[2][i] + nums[3][j]);
ans += e - s;
}
printf("%d\n", ans);
}
}
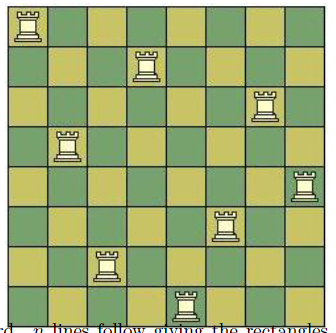
传说中的车（Fabled Rooks, UVa 11134）
国际象棋中车的行走方式和中国象棋一致，可以横向纵向走任意格。
输入输出
每组示例第一行是n，以下n行是第i个车可以放置的区间，输入以0结束。
对于每组示例，如果可以摆放，按顺序输出这i组车选择的xy坐标，如果无法摆放，输出IMPOSSIBLE
Sample Input
8
1 1 2 2
5 7 8 8
2 2 5 5
2 2 5 5
6 3 8 6
6 3 8 5
6 3 8 8
3 6 7 8
8
1 1 2 2
5 7 8 8
2 2 5 5
2 2 5 5
6 3 8 6
6 3 8 5
6 3 8 8
3 6 7 8
0
Sample Output
1 1
5 8
2 4
4 2
7 3
8 5
6 6
3 7
1 1
5 8
2 4
4 2
7 3
8 5
6 6
3 7
思路
xy是独立的，所以分开考虑。问题转换成执行两次从n个区间内找n个点，这些点不能相同，并且每个区间内都要选一个点。很巧妙。
贪心算法需要仔细考虑，我之前是按照左边界排序，左边界相同再按右边界排，选择当前区间中能选择的最小位置。但是这个策略对于[(1,3),(1,3),(2,2)]，这个贪心策略不满足，因为前两个选择了位置1和2，第三个无法选择。但是如果前两个选择1和3，第二个选择2，是满足要求的。
正确的贪心策略是按右边界排序，对于每个区间，搜索区间范围内最小的未被选择的点。
代码
单词拼错了，不重要。
#include "iostream"
#include "cstdio"
#include "cmath"
#include "vector"
#include <algorithm>
#include "cstring"
#define MAX 5000
#define X 0
#define Y 1
using namespace std;
struct Rect {
int xl, yl, xr, yr, id;
Rect(){}
Rect(int id):id(id) {}
}rects[MAX];
int ans[MAX][2];
int chosen[MAX];
int cmp_by_x(Rect &a,Rect &b) {
return a.xr < b.xr;
}
int cmp_by_y(Rect &a,Rect &b) {
return a.yr < b.yr;
}
bool choose(Rect &r,int axis) {
int lt = axis == X ? r.xl : r.yl;
int rt = axis == X ? r.xr : r.yr;
for (int i = lt; i <= rt; i++) {
if (!chosen[i]) {
chosen[i] = 1; ans[r.id][axis]=i;
return true;
}
}
return false;
}
int main() {
int n;
while (scanf("%d", &n) != EOF && n) {
memset(chosen, 0, sizeof(chosen));
for (int i = 0; i < n; i++) {
scanf("%d %d %d %d", &rects[i].xl, &rects[i].yl, &rects[i].xr, &rects[i].yr);
rects[i].id = i;
}
bool solved = true;
sort(rects, rects + n, cmp_by_x);
for (int i = 0; i < n; i++) {
if (!choose(rects[i], X)) {
solved = false; break;
}
}
if (solved) {
memset(chosen, 0, sizeof(chosen));
sort(rects, rects + n, cmp_by_y);
for (int i = 0; i < n; i++) {
if (!choose(rects[i], Y)) {
solved = false; break;
}
}
}
if (solved) {
for (int i = 0; i < n; i++)
printf("%d %d\n", ans[i][0], ans[i][1]);
}
else {
printf("IMPOSSIBLE\n");
}
}
return 0;
}
Gergovia的酒交易（Wine trading in Gergovia, UVa 11054）
直线上有\(n（2≤n≤100000）\)个等距的村庄，每个村庄要么买酒，要么卖酒。设第i个村庄对酒的需求为\(a_i（-1000≤a_i≤1000）\)，其中\(a_i>0\)表示买酒，\(a_i<0\)表示卖酒。所有村庄供需平衡，即所有\(a_i\)之和等于0。
把k个单位的酒从一个村庄运到相邻村庄需要k个单位的劳动力。计算最少需要多少劳动力可以满足所有村庄的需求。输出保证在64位带符号整数的范围内。
输入输出
Sample Input
5
5 -4 1 -3 1
6
-1000 -1000 -1000 1000 1000 1000
Sample Output
9
9000
思路
此题思路很巧妙，一句话概述之就是状态转换。此题在我还在刷LeetCode时就刷到过。
对于第一个村庄\(a_1\)，如果它买酒，就是\(a_1>0\)，那么它的酒必定是从\(a_2\)或更右侧运来的。不管后面如何，反正肯定有\(a_1\)瓶酒被从\(a_2\)运到\(a_1\)，那么这里的工作量就是\(a_1\)，然后\(a_2\)的需求量就是\(a_1+a_2\)，满足了\(a_1\)的需求量后，我们就不用考虑它了，转而把\(a_2\)看作第一个村庄，重复上面的过程。
而对于\(a_1\)，如果它卖酒，也就是\(a_1<0\)，那必定有\(a_1\)瓶酒被从\(a_1\)运到\(a_2\)，那么工作量也就是\(|a_1|\)，\(a_2\)的需求同样是\(a_1+a_2\)，同理，现在的工作量和\(a_1\)无关了，因为它的供需要求已经满足了，把\(a_2\)看作第一个村庄，重复。
代码
#include "iostream"
#include "cstdio"
#include "cmath"
#define LL long long
using namespace std;
int main() {
LL n,t;
while (scanf("%lld", &n),n) {
LL S = 0, W = 0;
for (int i = 0; i < n - 1; i++) {
scanf("%lld", &t);
S += t;
W += abs(S);
}
scanf("%lld", &t);
printf("%lld\n", W);
}
return 0;
}
唯一的雪花（Unique snowflakes, UVa 11572）
输入一个长度为\(n（n≤106）\)的序列A，找到一个尽量长的连续子序列\(A_L～A_R\)，使得该序 列中没有相同的元素。
输入输出
输入第一行是示例总数c。以下c组数据每组以一个数n开头，以下n行是该组输入序列。
对于每组输入序列，输出最长的无重复子序列。
Sample Input
1
5
1
2
3
2
1
Sample Output
3
思路
简单的滑动窗口。
维护一个窗口，每次向右拓宽窗口边界，当拓宽后窗口中出现重复字符时，左边界向右收紧，直至没有重复字符。重复以上过程直到遍历了整个字符串。
代码
#include "iostream"
#include "cstdio"
#include "vector"
#include "unordered_map"
using namespace std;
int max(int a,int b){
return a > b ? a : b;
}
int main() {
int kases;
scanf("%d", &kases);
for (int c = 0; c < kases; c++) {
int n,ans=0;
scanf("%d", &n);
unordered_map<int,int> have;
vector<int> seq(n);
for (int i = 0; i < n; i++) scanf("%d", &seq[i]);
int l = 0, r = 0;
while (r <= seq.size()) {
if (r == l) { r++; continue; }
int cpos = r-1,c = seq[cpos];
if (have.count(c) != 0) {
int older_pos = have[c];
for (int i = l; i <= older_pos; i++)have.erase(seq[i]);
l = older_pos + 1;
}
have[c] = cpos;
ans = max(ans, r - l);
r++;
}
printf("%d\n", ans);
}
return 0;
}
防线（Defense Lines, ACM/ICPC CERC 2010, UVa1471）
给一个长度为\(n（n≤200000）\)的序列，你的任务是删除一个连续子序列，使得剩下的序 列中有一个长度最大的连续递增子序列。例如，将序列{5, 3, 4, 9, 2, 8, 6, 7, 1}中的{9, 2, 8}删除，得到的序列{5, 3, 4, 6, 7, 1}中包含一个长度为4的连续递增子序列{3,4,6,7}。序列中每个数均为不超过\(10^9\)的正整数。
输入输出
输入第一行是数据组数，每组数据第一行是该组序列的长度n，第二行的n个数是序列。
对于每组输入，输出删除一个连续子序列能得到的最大连续递增子序列。
Sample Input
2
9
5 3 4 9 2 8 6 7 1
7
1 2 3 10 4 5 6
Sample Output
4
6
思路
首先，要删除一个连续子序列得到一个连续递增子序列，那么这个删除的序列是要把连续递增子序列分成两半的。
假设j是前面一半的最后一个，i是后面一半的第一个，中间是删除的子序列。那么最简单的办法就是遍历所有i，j。然后对于j，向前线性探测，直到前面的数构不成递增子序列，对于i则是向后探测。这个算法的时间复杂度是\(O(n^3)\)。
预处理优化，很多题目都会用到的一个技巧，看似简单却直接将时间复杂度降低一个指数级别。就是，对于每个A[i]，用一次正向遍历得到以这个数结尾的连续递增子序列的长度，为p(i)，再用一次反向遍历得到以这个数开头的连续递增子序列的长度，为r(i)，然后在我们的算法里就可以直接使用这些数据，而不用线性探测。复杂度下降为\(O(n^2)\)。
还是太大了。遍历i和j的所有组合肯定不行。紫书里提供的方法是过滤无用的数据，使得对于每个i，都能直接找到最合适的j，然后遍历i即可。
考虑一个事实，在序列中，假设j和j'都在i前面，如果\(A[j]>A[j'],p(j)<=p(j')\)的话，这个\(A[j]\)就不可能被选，因为对于i来说，\(A[j']\)始终是一个更好的选择，原因有二：
- 如果\(A[j']\)不能和\(A[i]\)构成连续递增子序列（前者比后者大），那么更大的\(A[j]\)更加不能。
- 如果二者都能和\(A[i]\)构成连续子序列，因为\(p(j')>=p(j)\)，所以选j'构成的序列不可能比选j构成的更短。
上面的说明可能很恶心，硬头皮想一下就好了。
使用一个二元组来记录这些\((A[j'],p(j'))\)。
这时我们让i从序列中第二个数开始遍历，我们用一个数据结构来按照上面的规则保存序列中它前面的数，这样我们只需要在前面的那些数里选择一个小于等于\(A[i]\)的最大数\(A[j]\)，经过上面的筛选，这个数必定是能构成最长的连续子序列需要的数，它的\(p(j)\)是序列中小于等于\(A[i]\)的数中最大的p。这样就得到了选择本个i时能得到的最大连续递增子序列。我们只需要找i为1,2,3,...,n里最大的那个即可。
那么对于i，往后移动时还要考虑如何把\(A[i]\)插入这个序列，因为对于\(A[i+1]\)，\(A[i]\)也是要考虑的，所有左边的数都要考虑。插入这个数时，要把所有大于它的并且p值小于等于它的数给删除。如果有两个\(A[i]\)，若待插入的\(p\)值比较小，就不用插入了，否则把序列中已经有的\(A[i]\)替换。
上面用到了查找，删除，插入，并且需要维护一个有序的序列，set可以实现这些功能。
代码
不知道AC没，Vjudge和UVA都坏了...
#include "iostream"
#include "cstdio"
#include "set"
using namespace std;
#define MAX 200000
int seq[MAX]; // 用于记录输入序列
int p[MAX], r[MAX]; // 对于每个元素，p记录它能向前延伸的最大个数，r记录向后的
int n;
struct Node {
int a, b;
Node(int a=0,int b=0):a(a),b(b){}
bool operator < (const Node& t) const {
return a < t.a;
}
};
int main() {
int kases;
scanf("%d", &kases);
for (int c = 0; c < kases; c++) {
scanf("%d", &n);
for (int i = 0; i < n; i++) {
scanf("%d", &seq[i]);
if (i == 0) p[i] = 1;
else if (seq[i] <= seq[i - 1])p[i] = 1;
else p[i] = p[i - 1] + 1;
}
r[n - 1] = 1;
for (int i = n - 2; i >= 0; i--) {
if (seq[i] > seq[i + 1])r[i] = 1;
else r[i] = r[i + 1] + 1;
}
// 照搬网上大佬的代码
set<Node> mp;
mp.insert(Node(seq[0], p[0]));
int ans = r[0];
for (int i = 1; i < n; i++) {
set<Node>::iterator it = mp.lower_bound(Node(seq[i], p[i]));
bool flag = true;
if (it != mp.begin()) {
Node t = *(--it);
ans = max(ans, t.b + r[i]);
if (t.b >= p[i])flag = false;
}
if (flag) {
Node t = Node(seq[i], p[i]);
mp.erase(t);
mp.insert(t);
it = mp.find(t); it++;
while (it != mp.end() && it->a > t.a && t.b >= it->b)mp.erase(it++);
}
}
printf("%d\n", ans);
}
return 0;
}
