递归和分治（算法竞赛入门经典）
循环日程表
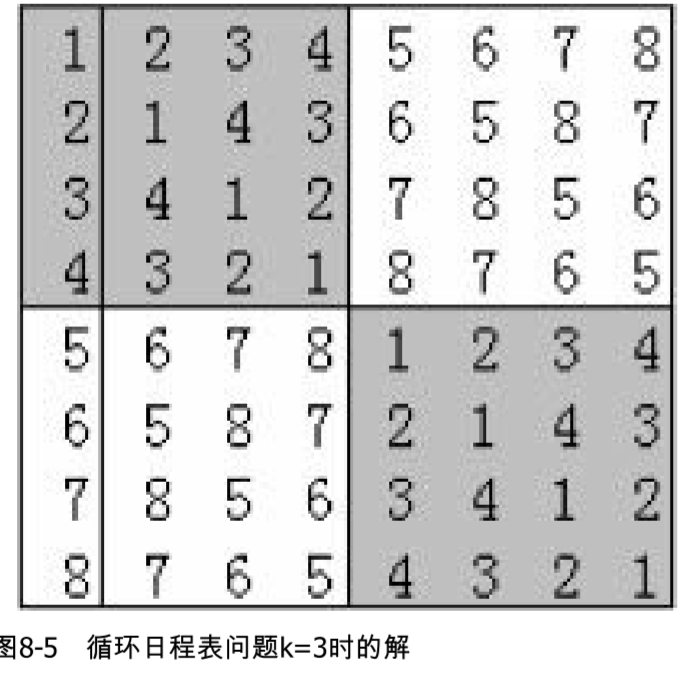
循环日程表问题。n=2k个运动员进行网球循环赛，需要设计比赛日程表。每个选手必 须与其他n-1个选手各赛一次；每个选手一天只能赛一次；循环赛一共进行n-1天。按此要求设计一张比赛日程表，该表有n行和n-1列，第i行j列为第i个选手第j天遇到的选手。
思路
此题可以使用递归策略，考虑当k=1时，有两个运动员，一下就能想出来
只需要让1和2配对，2和1配对即可。
1 2
2 1
k=2呢？第一天的配对我们可以轻松给出
1 2 ? ?
2 1 ? ?
3 4 ? ?
4 3 ? ?
在不改变我们之前以做的k=1时的选择的前提下，我们只能这样做，除此之外别无选择，因为每个选手每天只能比一次并且自己不能和自己比，也就是说一列和一行中都不能有重复的数字，我们把没重复数字的两块暂且称为互斥。1221和3443这两块互斥。
不难发现既然他俩互斥，那把3443复制到左上角，把1221复制到右下角，同样互斥。
1 2 3 4
2 1 4 3
3 4 1 2
4 3 2 1
这样就排好了k为2时的比赛表。
考虑3443和1221的关系，发现每个对应位都加上了k，所以可以得出对于\(2^k\)个运动员的比赛表，可以分解成四个\(2^{k-1}\)个运动员的比赛表，其中左下角可以有左上角加上\(2^{k-1}\)得到，右上角可以通过复制左下角得到，右下角可以通过复制左上角得到。直到k为1，我们把1221这个基本解填入。
代码
#include "iostream"
#include "cstdio"
#define MAXK 8
#define MAXTABLESIZE 256
using namespace std;
int table[MAXTABLESIZE][MAXTABLESIZE];
void generate_table(int k) {
if (k == 1) {
table[0][0] = 1; table[0][1] = 2; table[1][0] = 2; table[1][1] = 1;
return;
}
generate_table(k - 1);
int kk = 1 << (k - 1);
for (int i = 0;i < kk;i++) {
for (int j = 0; j < kk; j++) {
// 左下角 = 左上角 + kk
table[i+kk][j] = kk + table[i][j];
// 右上角 = 左下角
table[i][j + kk] = table[i + kk][j];
// 右下角 = 左上角
table[i + kk][j + kk] = table[i][j];
}
}
}
void show_table(int k) {
int kk = 1 << k;
for (int i = 0; i < kk; i++) {
cout << "Player " << table[i][0] << " : ";
for (int j = 1; j < kk; j++) {
cout << table[i][j] << " ";
}
cout << endl;
}
}
int main() {
generate_table(3);
show_table(3);
return 0;
}
巨人与鬼
巨人与鬼。在平面上有n个巨人和n个鬼，没有三者在同一条直线上。每个巨人需要选 择一个不同的鬼，向其发送质子流消灭它。质子流由巨人发射，沿直线行进，遇到鬼后消失。由于质子流交叉是很危险的，所有质子流经过的线段不能有交点。请设计一种给巨人和鬼配对的方法。
思路
这题真难，，，我是没思路。看的别人的。记一下吧。
拢共分三步。
- 找到左下角的点。
- 将其余所有点按照与此点的夹角排序，由于无三点共线，所以不存在有两个点和他的夹角相同的可能性。
- 遍历这些点，当左侧和右侧的巨人与鬼的数量相同时，将左下角的点和当前点配对，再递归求解左边和右边的点。
代码
这个代码写的贼丑并且不保证正确性，推荐别看了，看了降智商。
#include "iostream"
#include "cstdio"
#include "vector"
#include "cmath"
#include <algorithm>
using namespace std;
bool cmp_by_yx(vector<double> a,vector<double> b){
return a[1] < b[1] || (a[1] == b[1] && a[0]<b[0]);
}
bool cmp_by_ang(vector<double> a, vector<double>b) {
return a[3] < b[3];
}
void show_obj(vector<double> a) {
if (a[2])cout << "Human ";
else cout << "Devil ";
cout << "at the point [" << a[0] << "," << a[1] << "] ";
}
void solve(vector<vector<double>> objs) {
// 如果是最后两个 直接配对
if (objs.size() == 2) {
show_obj(objs[0]); cout << "bind to "; show_obj(objs[1]); cout << endl;
return;
}
// 算法有可能出现0个传进来的情况
if (objs.size() < 2)return;
// 左下角排序
sort(objs.begin(), objs.end(), cmp_by_yx);
// 拿出第一个
vector<double> base = objs[0]; objs.erase(objs.begin());
// 按夹角排序 arctan(tan(ang))
for (int i = 0; i < objs.size(); i++)
objs[i][3] = atan((objs[i][0] - base[0]) / (objs[i][1] - base[1]));
sort(objs.begin(), objs.end(), cmp_by_ang);
int hugeManCnt = 0, devilCnt = 0;
for (int i = 0; i < objs.size(); i++) {
if (hugeManCnt == devilCnt && hugeManCnt!=0) {
show_obj(base); cout << "bind to "; show_obj(objs[i]); cout << endl;
// 左
solve(vector<vector<double>>(objs.begin(), objs.begin()+i));
// 右
solve(vector<vector<double>>(objs.begin() + i + 1, objs.end()));
break;
}
hugeManCnt += objs[i][2];
devilCnt += !(objs[i][2]);
}
}
int main() {
vector<vector<double>> objs = {
{1,1,1,0},
{2,3,1,0},
{3,2,0,0},
{7,9,0,0}
};
solve(objs);
return 0;
}
