一些枚举题目（二）
埃及分数（Eg[y]ptian Fractions (HARD version), Rujia Liu's Present 6, UVa12558）
把a/b写成不同的埃及分数之和，要求项数尽量小，在此前提下最小的分数尽量大，然后第二小的分数尽量大……另外有k（0≤k≤5）个数不能用作分母。例如，k=0时\(5/121=1/33+1/121+1/363\)，不能使用33时最优解为\(5/121=1/45+1/55+1/1089\)。输入保证\(2≤a<b≤876，gcd(a,b)=1\)，且会挑选比较容易求解的数据。
输入输出
第一行输入是T，下面T行每行是一组输入示例，每行的前三个数是a,b,k。之后的k个数是不能用作分母的k个数。
Sample Input
5
2 3 0
19 45 0
2 3 1 2
5 121 0
5 121 1 3
Sample Output
Case 1: 2/3=1/2+1/6
Case 2: 19/45=1/5+1/6+1/18
Case 3: 2/3=1/3+1/4+1/12
Case 4: 5/121=1/33+1/121+1/363
Case 5: 5/121=1/45+1/55+1/1089
思路
之前做埃及分数的时候，由于这是紫书里介绍迭代加深的第一道题，在当时不了解迭代加深的原理再加上这题这么恶心的情况下，没咋明白。这回明白了。
思路详见代码注释
代码
#include "iostream"
#include "cstdio"
#include "cstring"
#include "cmath"
#include "set"
#define LL long long int
#define MAXK 5
#define MAXCS 100
using namespace std;
LL a, b,k,cs[MAXCS],ans[MAXCS];
set<int> ks; int cnt;
LL gcd(LL a, LL b) {
return b == 0 ? a : gcd(b, a % b);
}
/*
找到第一个满足1/c<a/b的c
1/c<a/b
c<b/a
所以c为b/a向上取整或者b/a+1
*/
LL first_smaller_than(LL aa, LL bb) {
return ceil(bb / (double)aa);
}
/*
因为题目中要求的是找到项数尽量小，最小的分数尽量大，第二小的分数尽量大...
所以先找到的答案可不一定是正确的，还得在此深度下继续查找
better判断当前的答案是否比已有答案更好
*/
bool better(int maxd) {
for (int i = maxd ; i >= 0; i--)
if (cs[i] != ans[i])return ans[i]==-1||cs[i] < ans[i];
return false;
}
/*
之前选择的是选择第d个1/c
最大选择maxd个1/c
当前离总目标a/b还差aa/bb
*/
bool dfs(int d,int maxd,LL first,LL aa, LL bb) {
// 如果深度等于最大深度
if (d == maxd) {
// 如果最后一个满足1/x的形式并且不在ks中
if (bb % aa || ks.count(bb / aa))return false;
cs[d] = bb / aa;
// 如比当前答案更好 更新
if (better(maxd)) {
memcpy(ans, cs, sizeof(cs));
return true;
}
return false;
}
first = max(first,first_smaller_than(aa,bb));
bool ok = false;
// 往后依次遍历每一个c
for (int c = first;; c++) {
// 如果c在ks里，不要
if (ks.count(c) != 0)continue;
// 如果后面的有限个都用1/c还是凑不够aa/bb，剪枝
if (bb*(maxd+1-d)<=aa*c)
break;
cs[d] = c;
// 算新的aabb，并通分
LL naa=aa*c-bb, nbb = bb*c;
LL g = gcd(nbb, naa);
if (dfs(d + 1, maxd,c+1, naa/g, nbb/g))ok = true;
}
return ok;
}
int main() {
int T;
scanf("%d", &T);
for (int kase = 1; kase <= T; kase++) {
scanf("%lld %lld %d", &a, &b, &k);
ks.clear();
for (int i = 0; i < k; i++) { int tmp; scanf("%d", &tmp); ks.insert(tmp); }
for (int maxd = 1;; maxd++) {
memset(ans, -1, sizeof(ans));
cnt = 0;
if (dfs(0, maxd,first_smaller_than(a,b), a, b)) {
printf("Case %d: %lld/%lld=", kase, a, b);
for (int j = 0; j <= maxd; j++) {
printf("1/%lld", ans[j]);
if (j < maxd)printf("+");
}
printf("\n");
break;
}
}
}
return 0;
}
数字谜（Digit Puzzle, ACM/ICPC Xi'an 2006,UVa12107）
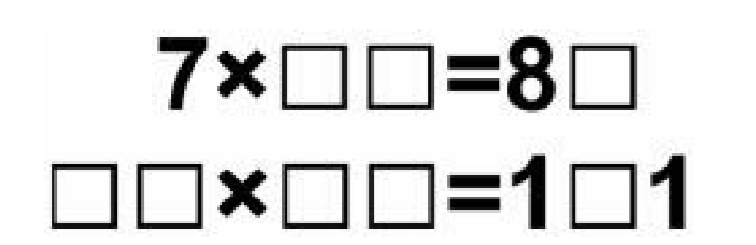
给出一个数字谜，要求修改尽量少的数，使修改后的数字谜只有唯一解。只有唯一解的数字谜称为“good pluzzle”。例如，如图7-30所示的两个数字谜就是“good pluzzle”。
修改指的是空格和数字可以随意替换，但不能增删。即空格换数字、数字换空格或数字 替换。数字谜中所有涉及的数必须是没有前导零的正数。输入数字谜一定形如a*b=c，其 中a、b、c分别最多有2、2、4位。
输入保证有解。如果有多种修改方案，则输出字典序最小的。字典序中空格小于数字。
输入输出
Sample Input
7 ** 8*
** ** ***
0
Sample Output
Case 1: 7 ** 8*
Case 2: ** ** 1*1
思路
两个dfs。
一个使用迭代加深来按字典序遍历修改的数，一个使用普通的bfs检测当前字符串是否已经是“good pluzzle”了。如果是就立即停止返回答案。
刚开始想到的也是这样，但是又觉得两个dfs怎么看都不太靠谱，后来实在想不出来别的办法，就上网查了一圈，发现大家也是两个dfs。还是题见的少。
代码
#include "iostream"
#include "cstring"
#include "cstdlib"
#include "cstdio"
using namespace std;
int lens[4] = { 0 };
char abc[3][5],abc2[3][5];
char modify[] = { '*','0','1','2','3','4','5','6','7','8','9' };
int good_cnt;
/*
填充所有星号 si是当前填充的第几个字符串，sj是当前字符串的第几个字符
*/
int good_puzzle(int si,int sj) {
int chk = 0;
if (si == 2) {// 前两个填满了，就可以计算前两个数字相乘是否可以得到第三个
int a = atoi(abc2[0]), b = atoi(abc2[1]);
char c[5];
sprintf(c, "%d", a * b);
if (strlen(c) != lens[3])return 0;
for (int i = 0; i < lens[3]; i++) {
if (abc[2][i] != '*' && abc[2][i] != c[i])
return 0;
}
return 1;
}
char old = abc[si][sj];
int new_si=si, new_sj=sj+1;
if (sj == lens[si + 1] - 1) { new_si=si+1; new_sj = 0; }
if (old == '*') {
for (int i = 1; i < 11; i++) {
// 无前导零
if (sj == 0 && modify[i] == '0')continue;
abc2[si][sj] = modify[i];
chk += good_puzzle(new_si, new_sj);
if (chk > 1)break;
}
}
else {
chk += good_puzzle(new_si, new_sj);
}
return chk;
}
/*
d是当前层数
maxd是最大层数
cur_arr是当前修改的数组，pos是修改的位置
*/
bool dfs(int d,int maxd,int cur_arr, int pos) {
good_cnt = 0;
memcpy(abc2, abc, sizeof(abc2));
if (d == maxd) {
return good_puzzle(0, 0) == 1;
}
if (cur_arr == 3)return false;
int new_cur_arr = cur_arr, new_pos=pos+1;
// 如果新位置走到字符串尾部了，换下一个字符串
if (new_pos == lens[cur_arr+1]) { new_cur_arr++; new_pos = 0; }
char old = abc[cur_arr][pos];
for (int i = 0; i < 11; i++) {
// 不能有前导零
if (pos == 0 && modify[i] == '0')continue;
// 没修改的情况
if (abc[cur_arr][pos] == modify[i]) {
if (dfs(d, maxd, new_cur_arr, new_pos))return true;
}
else {
abc[cur_arr][pos] = modify[i];
if (dfs(d+1,maxd,new_cur_arr, new_pos))return true;
}
abc[cur_arr][pos] = old;
}
return false;
}
int main() {
int n;
int kase = 1;
while (true) {
scanf("%s", abc[0]);
if (abc[0][0] == '0' && !abc[0][1])break;
scanf("%s %s", abc[1], abc[2]);
lens[1] = strlen(abc[0]); lens[2] = strlen(abc[1]); lens[3] = strlen(abc[2]);
for (int maxd = 0;; maxd++)
if (dfs(0, maxd, 0, 0))break;
printf("Case %d: %s %s %s\n",kase++,abc[0],abc[1],abc[2]);
}
return 0;
}
立体八数码问题（Cubic Eight-Puzzle , ACM/ICPC Japan 2006, UVa1604）
原题目链接：Aizu - 1268、UVa 1604
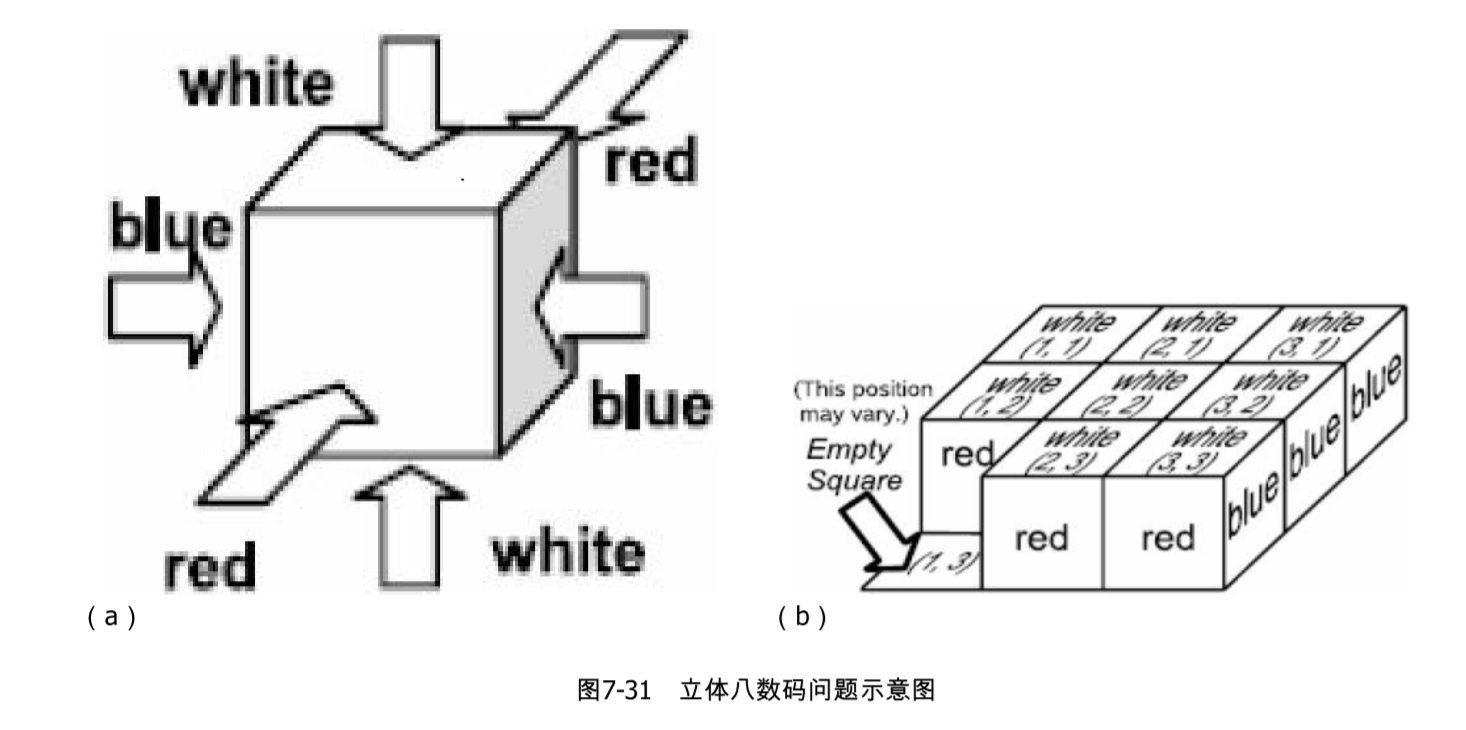
有8个立方体，按照相同方式着色（如图7-31（a）所示，相对的面总是着相同颜色）， 然后以相同的朝向摆成一个3*3的方阵，空出一个位置（如图7-31（b）所示，空位由输入决定）。
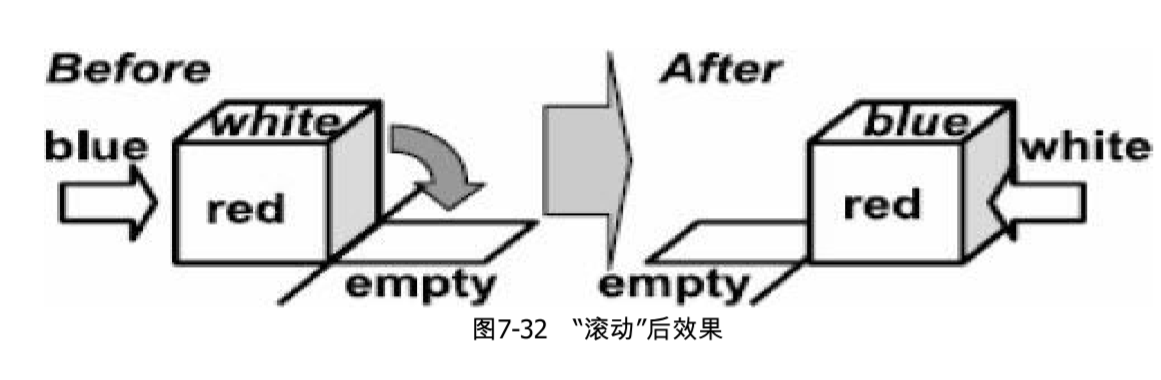
每次可以把一个立方体“滚动”一格进入空位，使它原来的位置成为空位，如图7-32所示。
你的任务是用最少的移动使得上表面呈现出指定的图案。输入空位的坐标和目标状态中 上表面各个位置的颜色，输出最小移动步数。
输入输出
有多组输入，每组的第一行由两个数字x，y组成，代表起始图案中空格的位置，而在起始图案中其他位置都是图(7-31)中的立方体。下面的3行3列矩阵是目标图案。以空格分隔。输入以0 0 结束
对于每组输入，如果能在30步之内（包括30）从起始状态移动得到目标状态，输出最小移动的步数，如果不能，输出-1。
Sample Input
1 2
W W W
E W W
W W W
2 1
R B W
R W W
E W W
3 3
W B W
B R E
R B R
3 3
B W R
B W R
B E R
2 1
B B B
B R B
B R E
1 1
R R R
W W W
R R E
2 1
R R R
B W B
R R E
3 2
R R R
W E W
R R R
0 0
Sample Output
0
3
13
23
29
30
-1
-1
思路
这题在学校的时候就肝了两天了，当时直接用的单个bfs，这样的话这道题目就和平面八数码差不多了，只是由于状态奇多无比，得近两分钟才能跑出结果。但是当时去网上看了别人的思路，已经知道该怎么做了，但是一直没时间做。今天做了一下，还是废了一天时间，真tm难。
而且可能是由于STL中自带的unordered_set的性能问题或者是Hash函数的设计问题，在UVa 3000ms的时间限制下，算法TLE了，但是对于所有已测试数据都能在3000ms左右出结果。
转而去Aizu上找到了一样的题，这里时间限制是8000ms，终于通过了。
思路就是双向bfs，从起始图案到目标图案搜索，另一个从最终目标图案到起始图案搜索，每次两个搜索都前进一层，当这两个搜索发现它们搜到了对方搜到过的东西，就代表二者已经到了相同的层，这时最终答案就是二者分别的步数和。
因为bfs每每加深一次，状态数就以指数级在增长，双向bfs从两端开始搜索，每次加深一层的话，两边都保持一个较小的深度，状态数不会太多。
要注意并仔细考虑的问题是，反向搜索怎么做。
给你如下的目标局面
W W W
E W W
W W W
左上角的立方体可能是如(7-31)中那样摆放的，也可能是将(7-31)中的立方体原地顺时针旋转90度那样摆放的，也就是blue朝前。因为答案要求的目标局面是一个俯视图，它不在乎侧面是什么样的，所以对于除了空格外的每一个位置，都有两个可能的摆放方式。所以肯定有\(2^8\)种摆放方式能得到目标局面。
那么就需要用一次dfs来获得这256个答案，并且全都放在第二个bfs的队列中。
由于正向和反向bfs初始数据量的差异，将二者的最大深度限制为15总不是那么好的，网上经测试得到最优的次数限制是正向21次，反向9次，我们直接用吧。
代码
#include "iostream"
#include "cstdio"
#include "cstring"
#include <unordered_set>
#include <queue>
#define LEFT 1
#define UP 2
#define RIGHT 3
#define DOWN 4
#define IN_PLACE 5
#define HASH_SIZE 1000007
using namespace std;
const char initialSt[] = "WBWBRR";
struct Cube {
int dir;
// 记录正方体的六个面
char st[6];
Cube() { new(this)Cube(-1); }
Cube(int dir): dir(dir) {memcpy(this->st, initialSt, sizeof(this->st));}
Cube(int dir,const Cube & src):dir(dir) { memcpy(this->st,src.st,sizeof(this->st));}
void _swap(int i, int j) {
char t = st[i]; st[i] = st[j]; st[j] = t;
}
/*
向一个方向转，1左，2上，3右，4下
*/
Cube rotate(int dir) {
Cube newCube = Cube(*this);
if (dir == LEFT) {
newCube._swap(0, 1); newCube._swap(1, 2); newCube._swap(2, 3);
}
else if (dir == RIGHT) {
newCube._swap(0, 3); newCube._swap(3, 2); newCube._swap(2, 1);
}
else if (dir == UP) {
newCube._swap(4, 0); newCube._swap(2, 4); newCube._swap(5, 2);
}
else if (dir == DOWN) {
newCube._swap(5, 0); newCube._swap(2, 5); newCube._swap(4, 2);
}
else if (dir == IN_PLACE) {
newCube._swap(4, 1); newCube._swap(1, 5); newCube._swap(5, 3);
}
return newCube;
}
};
struct Board {
int epos;
int step;
Cube cubes[9];
Board(int epos,int step) : epos(epos),step(step){}
Board(int epos,int step, Cube cubes[]) : epos(epos),step(step){
memcpy(this->cubes, cubes,sizeof(this->cubes));
}
bool operator == (const Board& t)const {
if (this->epos != t.epos)return false;
for (int i = 0; i < 9; i++) {
if (i == epos)continue;
for (int j = 0; j < 6;j++) {
if (this->cubes[i].st[j] != t.cubes[i].st[j])return false;
}
}
return true;
}
};
int get_val(char a) {
return a == 'W' ? 1 : a == 'R' ? 2 : 3;
}
struct BoardHash {
size_t operator () (const Board& t) const {
int hash = 0;
for (int i = 0; i < 9; i++) {
int delta = 0;
if (i != t.epos) delta = get_val(t.cubes[i].st[0]);
hash += hash * 10 + delta;
}
//printf("%d\n", hash);
return hash % HASH_SIZE;
}
};
unordered_set<Board, BoardHash> h1, h2;
int target_epos;
char target[9];
Cube W, B = W.rotate(LEFT), R = W.rotate(UP);
queue<Board> q1, q2;
void readTarget() {
getchar();
for (int i = 0; i < 9; i++) {
target[i] = getchar();
if (target[i] == 'E')target_epos = i;
getchar();
}
}
void fillQ2(int idx,Board cur) {
if (idx == 9) {
Board b(cur.epos,0, cur.cubes);
h2.insert(b);
q2.push(b);
return;
}
Cube cube;
if (target[idx] == 'E') {
cur.cubes[idx] = cube;
fillQ2(idx + 1, cur);
}
else {
if (target[idx] == 'W') { cube = W; }
else if (target[idx] == 'R') { cube = R; }
else if (target[idx] == 'B') { cube = B; }
cur.cubes[idx] = cube;
fillQ2(idx + 1, cur);
cur.cubes[idx] = cur.cubes[idx].rotate(IN_PLACE);
fillQ2(idx + 1, cur);
}
}
// 右下左上 与上面的记录恰好相反，原因是对于左边的格子，它则需要右转才能进入到空白
int dy []= { 1,0,-1,0 }, dx[] = { 0,1,0,-1 };
bool wc(Board& b) {
int cnt = b.epos==target_epos ? 0:2;
for (int i = 0; i < 9; i++) {
if (i == target_epos || i == b.epos)continue;
int top = b.cubes[i].st[0];
if (top != target[i])cnt++;
}
return cnt;
}
void bfs(Board initial){
q1.push(initial);
h1.insert(initial);
fillQ2(0,Board(target_epos,0));
// 双向bfs，每次每个方向深入一层，当二者相撞时，答案等于二者分别走过的步数和。当二者错过，答案不存在。
int cnt1 = 0, cnt2 = 0;
while (true) {
bool hasMore = false;
while (!q1.empty() && q1.front().step <= cnt1) {
hasMore = true;
Board b = q1.front(); q1.pop();
if (h2.count(b) != 0) {
// findit
printf("%d\n", b.step + cnt2);
return;
}
// 如果错误的位置甚至要比剩余可走的步数之内能归位的数码数还大 n步最多可让n+1个归位
if (wc(b) > 30 - b.step +1) continue;
int ex = b.epos/3, ey = b.epos % 3;
// 选择空白方块周围的方块
for (int i = 0; i < 4; i++) {
// 经过一二维坐标转换，计算出新的一维空白位置，然后便是把它旋转并和之前的空白位置互换
int newx = ex + dx[i], newy = ey + dy[i];
if (newx >= 0 && newx < 3 && newy >= 0 && newy < 3 && b.step<21) { // 一定要判断这个step，否则会出错
int newpos = newx * 3 + newy;
Board newb(newpos,b.step+1,b.cubes);
Cube c = b.cubes[newpos].rotate(i + 1);
newb.cubes[newpos] = newb.cubes[b.epos];
newb.cubes[b.epos] = c;
if (h1.count(newb) != 0)continue;
q1.push(newb);
h1.insert(newb);
}
}
}
if (cnt1 < 21)cnt1++;
while (!q2.empty() && q2.front().step <= cnt2) {
hasMore = true;
Board b = q2.front(); q2.pop();
if (h1.count(b) != 0) {
printf("%d\n", b.step + cnt1);
return;
}
if (wc(b) > 30 - b.step + 1)
continue;
int ex = b.epos / 3, ey = b.epos % 3;
for (int i = 0; i < 4; i++) {
int newx = ex + dx[i], newy = ey + dy[i];
if (newx >= 0 && newx < 3 && newy >= 0 && newy < 3 && b.step<9) {
int newpos = newx * 3 + newy;
Board newb(newpos, b.step + 1, b.cubes);
Cube c = b.cubes[newpos].rotate(i + 1);
newb.cubes[newpos] = newb.cubes[b.epos];
newb.cubes[b.epos] = c;
if (h2.count(newb) != 0)continue;
q2.push(newb);
h2.insert(newb);
}
}
}
if (cnt2 < 9)cnt2++;
if (!hasMore) {
printf("-1\n"); return;
}
}
}
void clear() {
h1.clear(); h2.clear();
while (!q1.empty())q1.pop();
while (!q2.empty())q2.pop();
}
int main() {
int x,y;
while (scanf("%d %d", &y,&x) != EOF && x && y) {
x--; y--;
Board initial(x*3+y,0);
readTarget();
bfs(initial);
clear();
}
return 0;
}
操他妈的，累死了，饿死了，拜拜。
守卫棋盘（Guarding the Chessboard, UVa11214）
给你一个\(n *m\)的棋盘，这个棋盘的格子被一些正方形标记了，你需要放置尽可能少的皇后使得它们能攻击到所有被标记正方形的格子。如下是一个所有格子都被标记了的\(8*8\)棋盘的一个解。（注意皇后可以放置在未被标记的棋盘上）。
输入输出
包含最多15个测试示例，每个由包含两个整数的行开始，分别是\(n,m(1<n,m<10)\)，代表棋盘的大小。后面n行包含m个字符，X代表该格子被标记了，.代表该格子没被标记。最后一个示例以0结束。
对于每个示例，输出最小需要摆放的皇后数。
Sample Input
8 8
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
XXXXXXXX
8 8
X.......
.X......
..X.....
...X....
....X...
.....X..
......X.
.......X
0
Sample Output
Case 1: 5
Case 2: 1
思路
这题不难，由于不知道最大深度（实际不会超过5），使用IDA*实现（其实没有A*只是普通的迭代加深）。和上一题不是一个级别啊。
代码
直接上代码吧，还有就是紫书里用来处理对角线的方法真不错，之前写八皇后的时候没细看是硬写的。
#include "iostream"
#include "cstdio"
#include "cstring"
using namespace std;
char board[10][10];
int vis[4][2 * 10];
// 因为一个皇后会占用整行，整列和两整条对角线，
// 所以vis[0][r]用于存储第r行的占用情况，vis[1]
// vis[1][c]用于存储第c列的占用情况
// vis[2][c+r]用于存储反对角线，因为反对角线的xy坐标相加都是相同的
// vis[3][c-r+n]用于存储正对角，因为正对角线的xy坐标相减都是相同的，但有可能出现负数，所以加n
int n, m,kase=1;
bool check() {
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (board[i][j] == 'X' && !(vis[0][i] || vis[1][j] || vis[2][i + j] || vis[3][j - i + n])) {
return false;
}
}
}
return true;
}
bool dfs(int maxd, int d, int r) {
if (d == maxd) {
if (check())return true;
return false;
}
for (int row = r; row < n; row++) {
for (int col = 0; col < m; col++) {
int t1, t2, t3, t4;
t1 = vis[0][row]; t2 = vis[1][col]; t3 = vis[2][col + row]; t4 = vis[3][col - row + n];
vis[0][row] = vis[1][col] = vis[2][col + row] = vis[3][col - row + n] = 1;
if (dfs(maxd, d + 1, row + 1))return true;
vis[0][row] = t1; vis[1][col] = t2; vis[2][col + row] = t3; vis[3][col - row + n] = t4;
}
}
return false;
}
int main() {
while (scanf("%d %d", &n,&m) == 2 && n && m) {
getchar();
memset(vis, 0, sizeof(vis));
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) board[i][j] = getchar();
getchar();
}
for (int maxd = 0; ; maxd++) {
if (dfs(maxd, 0, 0)) {
printf("Case %d: %d\n", kase++, maxd);
break;
}
}
}
return 0;
}
