一些枚举题目
宝箱（Zombie's Treasure Chest, Shanghai 2011, UVa12325）
你有一个体积为N的箱子和两种数量无限的宝物。宝物1的体积为S1，价值为V1；宝物2的体积为S2，价值为V2。输入均为32位带符号整数。你的任务是计算最多能装多大价值的宝物。例如，n=100，S1=V1=34，S2=5，V2=3，答案为86，方案是装两个宝物1，再装6个宝物2。每种宝物都必须拿非负整数个。
输入输出
有多组输入输出，输入的第一行是一个整数T(T<=200)，接下来的T行每行是一组输入，有五个整数，分别是N,S1,V1,S2,V2。它们都是32位的正整数。
对于每组输入，输出组数和最多能装的数量。
Sample Input
2
100 1 1 2 2
100 34 34 5 3
Sample Output
Case #1: 100
Case #2: 86
思路
刚开始以为是贪心，算的单位体积的价值\(V/S\)，优先装单位价值大的，装不下再选择小的。这是错误的想法，很容易找出反例。
比如如下序列
12 8 8 6 5
V1/S1 = 1 , V2/S2 = 0.83
贪心会选择一个第一个宝物 1 * 8 = 8
而实际上最优的选择是两个第二个宝物 2 * 5 = 10
还是得考虑所有情况，使用枚举法。
我们可以枚举第一个宝物的个数i，然后再算出选择i个第一个宝物后还可以装的第二个的个数，从而算出一个最大的。
代码
#include "iostream"
#include "cstdio"
#define LL long long int
using namespace std;
LL max(LL a, LL b) {
return a > b ? a : b;
}
int main() {
int T;
LL max_v;
LL n, s1, v1, s2, v2;
scanf("%d", &T);
int kase = 1;
while (kase <= T) {
max_v = 0;
cin >> n >> s1 >> v1 >> s2 >> v2;
for (LL i = 0; s1 * i <= n; i++) {
LL s2_cnt = (n - s1 * i) / s2;
max_v = max(i * v1 + s2_cnt * v2, max_v);
}
cout << "Case #" << kase++ << ": " << max_v << endl;
}
return 0;
}
会出现一个极端情况，如果n特别大，s1特别小的话，枚举s1不如枚举s2来的实惠，所以我们判断一下s1是不是小于s2，如果是就交换他俩。
if (s1<s2) {
swap(s1, s2); swap(v1, v2);
}
...
还有一种情况是，n特别大，s1和s2都很小，这时候用s1和s2都会循环很久，因为题目中给的n可能很大。
这就需要另外一个比较有意思的想法，有一个事实是，s1个宝物2和s2个宝物1的体积相等，因为\(s1*s2=s2*s1\)。这时候如果选s1个宝物2的价值比选s2个宝物1的价值高的话，我们能断定，宝物2最多选择s1-1个，因为如果最优选择里有s1个宝物2，那么就可以用一个更优的s2个宝物1替换，这和这已经是最优选择的事实相矛盾，所以上述结论成立。
通过这三种分类枚举，可以避免因为极端情况造成的算法性能急剧下降。
代码
最终代码如下：
#include "iostream"
#include "cstdio"
#define LL long long int
using namespace std;
void swap(LL* a, LL* b) {
LL t = *a; *a = *b; *b = t;
}
LL max(LL a, LL b) {
return a > b ? a : b;
}
int main() {
int T;
LL max_v;
LL n, s1, v1, s2, v2;
scanf("%d", &T);
int kase = 1;
while (kase <= T) {
max_v = 0;
cin >> n >> s1 >> v1 >> s2 >> v2;
// 当s1和s2<<n时，使用其他策略
if (s1 * s2 <= n) {
// s2个宝物1 与 s1个宝物2 体积相等 ，价值分别为 s2*v1 , s1*v2
// 这时 如果选s2个宝物1得到的价值比选s1个宝物2要高，那么最多只能选择s1-1个宝物2，因为s1个宝物2可以用价值更高的s2个宝物1代替
// 反之一样，为方便，交换s1v1，s2v2把第二种情况转换为第一种
// 所以循环s2的个数即可
if (s2*v1<s1*v2) {
swap(s1, s2); swap(v1, v2);
}
for (int i = 0; i <= s1 - 1; i++) {
int s1_cnt = (n - i * s2) / s1;
max_v = max(i * v2 + s1_cnt * v1, max_v);
}
}
else {
// 在原来的s1和s2中选一个离N最近的做新s1 加速递归
if (s1<s2) {
swap(s1, s2); swap(v1, v2);
}
// 遍历s1的个数
for (LL i = 0; s1 * i <= n; i++) {
LL s2_cnt = (n - s1 * i) / s2;
max_v = max(i * v1 + s2_cnt * v2, max_v);
}
}
cout << "Case #" << kase++ << ": " << max_v << endl;
}
return 0;
}
旋转游戏（The Rotation Game, Shanghai 2004, UVa1343）
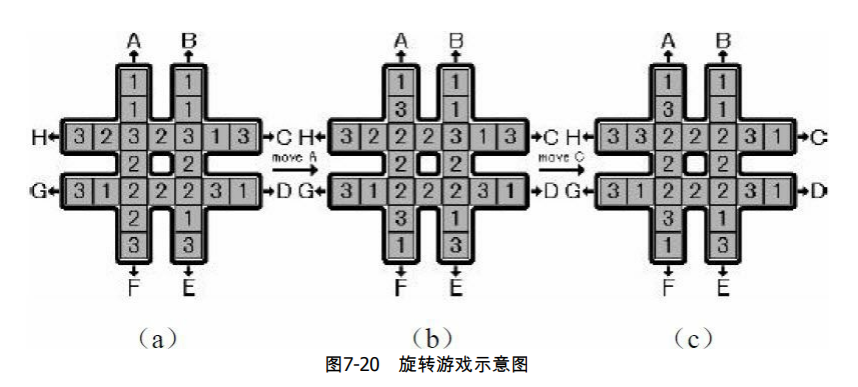
如图7-20所示形状的棋盘上分别有8个1、2、3，要往A～H方向旋转棋盘，使中间8个方格数字相同。图7-20（a）进行A操作后变为图7-20（b），再进行C操作后变为图7-20（c），这正是一个目标状态（因为中间8个方格数字相同）。要求旋转次数最少。如果有多解，操作序列的字典序应尽量小。
输入输出
Sample Input
1 1 1 1 3 2 3 2 3 1 3 2 2 3 1 2 2 2 3 1 2 1 3 3
1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 3 3 3 3 3 3 3 3
0
Sample Output
AC
2
DDHH
2
思路
尝试了用BFS，也像刘汝佳大佬说的一样把三个数字的状态分开处理了。不排除是我压缩状态的时候出了问题，反正当答案需要的搜索深度特别高的时候基本废了。
使用IDA*最后AC了。
思路就是使用当前棋盘作为状态，每次遍历按照字典序做这八种旋转操作，生成新状态，然后加深深度继续旋转这些新状态，直到找到一个状态满足中间八个方格数字相同，这个即为答案。
关于启发函数，考虑中间八个位置的数字c，每次最多能把一个数字旋转到这八个格子中，如果当前深度是d，最大深度是maxd，那也就是说如果d+c>maxd，就可以进行剪枝操作。
代码
这代码很丑也很慢，勉强AC。
网上的代码有把状态编码成一维数组然后用一些辅助操作的数组来实现访问的，会快很多并且清淅很多。
#include "iostream"
#include "cstdio"
#include "cstring"
#include "string"
#include "queue"
using namespace std;
typedef int State[7][7];
int dr[8] = { -1,-1,2,4,-1,-1,4,2 };
int dc[8] = { 2,4,-1,-1,4,2,-1,-1 };
int dd[8] = { -1,-1,1,1,1,1,-1,-1 };
char letter[8] = { 'A','B','C','D','E','F','G','H' };
deque<char> ans;
State initial;
bool read() {
memset(initial, 0, sizeof(initial));
for (int i = 1; i <= 7; i++)
for (int j = 1; j <= 7; j++)
if (i== 3|| i == 5 || j == 3 || j ==5) {
scanf("%d", &initial[i-1][j-1]);
if (!initial[i-1][j-1])return false;
}
return true;
}
bool check(State &st) {
int t = -1;
for (int i = 3; i <= 5; i++) {
for (int j = 3; j <= 5; j++) {
if (i==4&&j==4)continue;
if (t == -1)t = st[i - 1][j - 1];
else if (st[i - 1][j - 1] != t)return false;
}
}
return true;
}
int h(State &st) {
int n1, n2, n3; n1 = n2 = n3 = 0;
for (int i = 3; i <= 5; i++) {
for (int j = 3; j <= 5; j++) {
if (i == 4 && j == 4)continue;
int num = st[i - 1][j - 1];
if (num != 1)n1++; if (num != 2)n2++; if (num != 3)n3++;
}
}
return min(min(n1,n2),n3);
}
bool dfs(State & cur,int d,int maxd) {
if (d + h(cur) > maxd)return false;
if (check(cur)) {
// 把最终结果加到ans
ans.push_back(cur[2][2]);
return true;
}
for (int i = 0; i < 8; i++) {
State st;
memcpy(st,cur,sizeof(st));
if (dr[i] != -1) {
if (dd[i] == -1) {
int t = st[dr[i]][0];
for (int j = 1; j < 7; j++)st[dr[i]][j-1] = st[dr[i]][j];
st[dr[i]][6] = t;
}
else {
int t = st[dr[i]][6];
for (int j = 5; j >= 0; j--)st[dr[i]][j + 1] = st[dr[i]][j];
st[dr[i]][0] = t;
}
}
else {
if (dd[i] == -1) {
int t = st[0][dc[i]];
for (int j = 1; j < 7; j++)st[j-1][dc[i]] = st[j][dc[i]];
st[6][dc[i]] = t;
}
else {
int t = st[6][dc[i]];
for (int j = 5; j >= 0; j--) st[j + 1][dc[i]] = st[j][dc[i]];
st[0][dc[i]] = t;
}
}
ans.push_back(letter[i]);
if (dfs(st, d + 1, maxd)) {
return true;
}
ans.pop_back();
}
return false;
}
int main() {
while (read()) {
ans.clear();
// 输入即满足
if (check(initial)) {
printf("No moves needed\n%d\n",initial[2][2]);
continue;
}
// 迭代加深
for (int maxd = 1;; maxd++)
if (dfs(initial, 0, maxd)) {
// 打印结果
int g = ans.back();
ans.pop_back();
while (!ans.empty()) {
cout << ans.front();
ans.pop_front();
}
cout << endl<<g<<endl;
break;
}
}
return 0;
}
快速幂计算（Power Calculus, ACM/ICPC Yokohama 2006, UVa1374）
输入输出
Sample Input
1
31
70
91
473
512
811
953
Sample Output
0
6
8
9
11
9
13
12
思路
快速幂即把一个大的求幂运算分解成两个更小的求幂运算的过程，比如\(9^5=（81^2）*(9^1)\)
为了加深理解可以先去做一下航电一百题里的一道题：HOJ-2035
对于这道题，使用IDA*来求解，状态就是当前选择的指数的集合，我们要做的就是看看使用这些指数能不能组合成题目中的输入，如果能，当前最大深度就是答案，如果不能，加深。
关于启发函数，我们设\(g\)为当前指数集合里最大的那个指数，当前深度为\(d\)，最大深度为\(maxd\)，那么我们能组合出来的最大指数就是后面几层都选择这个最大的指数，即\(2^{maxd-d} \times g\)，如果这都小于\(n\)，就证明后面无论怎样组合都到不了\(n\)，可以剪枝。
代码如下
#include "iostream"
#include "cstdio"
#define MAX 20
using namespace std;
int st[MAX] = { 1 };
int n;
int get_max(int d) {
int max = 0;
for(int i=d-1;i>=0;i--){
if (max < st[i])max = st[i];
}
return max;
}
bool have(int t,int d) {
for (int i = d-1; i >= 0; i--) {
if (st[i] == t)return true;
}
return false;
}
bool dfs(int d, int maxd) {
if (d>maxd || (1 << (maxd-d))*get_max(d) < n)return false;
if (st[d-1] == n){
return true;
}
for (int i = d - 1; i >=0 ;i--) {
if (!have(st[i]+st[d-1],d)) {
st[d] = st[i] + st[d-1];
if (dfs(d + 1, maxd))return true;
}
if (!have(st[i]-st[d-1],d) && st[d-1]-st[i] > 0) {
st[d] = st[d-1] - st[i];
if (dfs(d + 1, maxd))return true;
}
}
return false;
}
int main() {
while (scanf("%d", &n) != EOF && n!=0) {
for (int maxd = 0;; maxd++) {
if (dfs(1, maxd)) {
printf("%d\n", maxd-1);
break;
}
}
}
return 0;
}
网格动物（Lattice Animals, ACM/ICPC NEERC 2004, UVa1602）
输入输出
Sample Input
5 1 4
5 2 4
5 3 4
5 5 5
8 3 3
Sample Output
0
5
11
12
3
思路
拿到题目想了很久，也没想出个啥思路。
但是有了一些启发，就是对于此题，我们只考虑形状，无需考虑位置，也就是所有n连块都是在左上角的，然后看这个形状能不能被\(w\times h\)的矩形装下。题目中有一些很操蛋的设定，就是平移、旋转、翻转操作之后的n连块算同一个，这就给去重带来了很大的麻烦。我最初的设想是对于每一个块，把它插入到vis数组中的时候就把那些操作能得到的所有n连块都一同插进去，但是显然不能用数组。还有就是既然不考虑位置了，那平移操作怎么解决？
下面的代码是按照大佬的抄的
思想是对于每一个n，计算出所有的不重复并且不能通过题目中的操作变成相等的块的n连块，然后再计算所有的n、w、h下的所有答案，打成表。具体思路在下面的代码注释中
代码
#include "iostream"
#include "cstdio"
#include "set"
#define MAX 11
using namespace std;
// 一个正方形，组成n连块的一个元素
struct Cell {
int x, y;
Cell(int x, int y) :x(x), y(y) {}
bool operator < (const Cell& rhs)const {
return x < rhs.x || (x == rhs.x && y < rhs.y);
}
};
// 正方形的集合，即一个n连块
typedef set<Cell> Polyomino;
// N连块的集合数组 Polys[i]即代表所有i连块的集合
set<Polyomino> Polys[MAX];
// 答案表
int ans[MAX][MAX][MAX];
#define FOR_CELL(c,p) for(set<Cell>::const_iterator c = (p).begin(); c != (p).end(); ++c)
#define FOR_POLY(c,p) for(set<Polyomino>::iterator c = (p).begin(); c != (p).end(); ++c)
int N, W, H;
int dx[] = { -1, 1, 0, 0 };
int dy[] = { 0, 0, -1, 1 };
/*
标准化将n连块放到左上角
*/
Polyomino normalize(const Polyomino& p) {
Polyomino q;
int minX = p.begin()->x, minY = p.begin()->y;
FOR_CELL(c, p) {
minX = min(minX, c->x);
minY = min(minY, c->y);
}
FOR_CELL(c, p) {
q.insert(Cell(c->x - minX, c->y - minY));
}
return q;
}
/*
将n连块旋转90度
*/
Polyomino rotate(const Polyomino& p) {
Polyomino q;
FOR_CELL(c, p) {
q.insert(Cell(c->y, -c->x));
}
return normalize(q);
}
/*
将n连块按x轴翻转
*/
Polyomino flip(const Polyomino& p) {
Polyomino q;
FOR_CELL(c, p) {
q.insert(Cell(c->x, -c->y));
}
return normalize(q);
}
bool alreadyInFourDir(Polyomino& p, const int& n) {
for (int i = 0; i < 4; ++i) {
if (Polys[n].count(p) != 0)return false;
p = rotate(p);
}
return true;
}
/*
在n连块 p中插入正方形c
会检测当前能通过平移、旋转、翻转操作后等价于c的正方形
如果没有再插入
*/
void checkAndInsertPolyomino(const Polyomino& p,const Cell& c) {
Polyomino q = p; // 复制原n连块
q.insert(c); // 插入这个单元格
q = normalize(q); // 标准化使q在左上角
int n = q.size();
// 查看集合中有没有能通过四个旋转操作得到的正方形
if (!alreadyInFourDir(q, n))return;
// 按x轴翻转
q = flip(q);
// 查看翻转后的情况，因为按y轴翻转等于按x轴翻转再旋转180，所以不用检测y
if (!alreadyInFourDir(q, n))return;
// 无误后插入
Polys[n].insert(q);
}
void generate() {
// 当n为1的时候，只有一种情况，一个正方形在0，0
// 给定这种初始情况，并且所有后继情况是根据初始情况算出来的
Polyomino p;
p.insert(Cell(0, 0));
Polys[1].insert(p);
for (int n = 2; n < MAX; n++) {
// 遍历n-1情况下所有的n连块
FOR_POLY(s, Polys[n - 1]) {
// 遍历n连块中的每个正方形
FOR_CELL(c, *s) {
for (int i = 0; i < 4; i++) {
// 尝试在四面接一个正方形
Cell newc(c->x + dx[i], c->y + dy[i]);
// 这时接的正方形有可能和原n连块中的重叠
// 判断一下，如果不重叠就进入平移旋转反转的检测
if ((*s).count(newc) == 0) checkAndInsertPolyomino(*s, newc);
}
}
}
}
// 打答案表
for (int n = 1; n < MAX; n++) {
for (int w = 1; w < MAX; w++) {
for (int h = 1; h < MAX; h++) {
int cnt = 0;
FOR_POLY(s, Polys[n]) {
int maxX=0, maxY=0;
FOR_CELL(c, *s) {
maxX = max(maxX, c->x);
maxY = max(maxY, c->y);
}
if (min(h, w) > min(maxX, maxY) && max(h, w) > max(maxX, maxY)) cnt++;
}
ans[n][w][h] = cnt;
}
}
}
}
int main() {
// 先打表
generate();
while (scanf("%d %d %d", &N,&W,&H) != EOF) {
// 直接查表
printf("%d\n", ans[N][W][H]);
}
return 0;
}
破坏正方形（Square Destroyer, ACM/ICPC Taejon 2001, UVa1603）
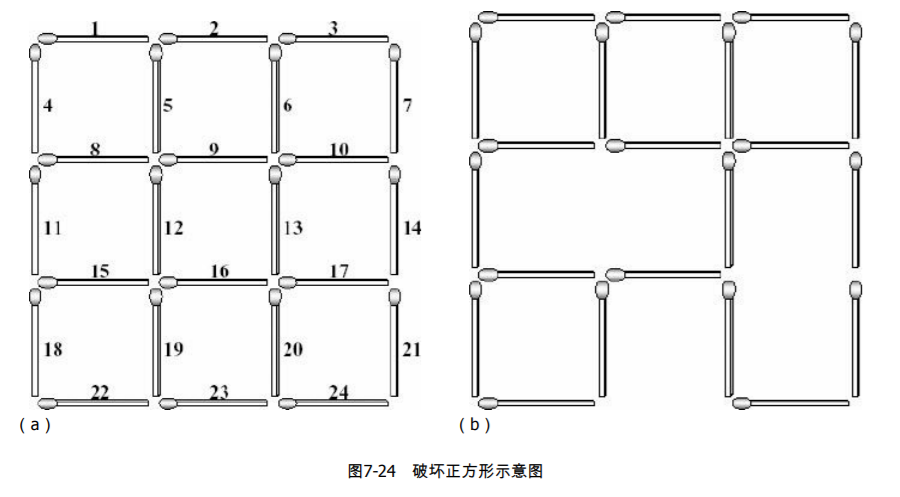
有一个火柴棍组成的正方形网格，每条边有n根火柴，共\(2n(n+1)\)根。从上到下、从左到右给各个火柴编号，如图7-24（a）所示。现在拿走一些火柴，问在剩下的火柴中，至少还要拿走多少根火柴才能破坏所有正方形？例如，在图7-24（b）中，拿掉3根火柴就可以破坏掉仅有的5个正方形。
输入输出
输入的第一行是一个正整数T，下面的T组输入每组的第一行是一个正整数n，也就是题目中的n，\(n\le 5\)，每组的第二行第一个数是k，代表有几根火柴是已经被拿走的，余下的k个数是被拿走火柴的编号。
对于每组输入，输出至少还要拿走多少根火柴才能破坏掉所有正方形。
Sample Input
2
2
0
3
3 12 17 23
Sample Output
3
3
思路
其实题目不难，迭代加深很好解。关键是和上一题一样，这个题目问的问题需要用什么样的数据结构来存储，怎样存。这不太好想，对于我来说不太好想。
也是和上一题一样，按网上的看，看明白之后自己按照那个思路来写。
思路就是把火柴和正方形编号，当然，火柴本来就是有编号的，我们需要遵循这个。。。不怎么好用的编号规则（这个编号规则也是卡住我的地方），然后就是正方形编号，我们就用顺序编号就行，然后每次找一个没被破坏的正方形，拿组成这个正方形的一根火柴，破坏掉这个正方形，并且把这根火柴能破坏的其他正方形也破坏。也就是每层深度代表拿掉一根火柴，每次加深深度时检测是不是所有正方形都被破坏，如果是直接可以返回了。
需要注意的是，也是困难的地方是有边长为\(1,2,3,...,n\)的正方形，这些都要编进去。如下：
注意，会有\(n^2\)个边长为1的正方形，有\((n-1)^2\)个边长为2的正方形，依此类推，直到\((n-(n-1))^2\)个边长为n的正方形。
对于启发函数，这里我和网上的不一样，我的没有它的高性能，但是也AC了。我就说说我的，它的我后面放链接。
我的想法很奇怪，依赖n的大小，就是当n为1时，拿走一根火柴最多破坏1个正方形，当n为2时，一根火柴最多破坏2个，n为3时就是4个，n最多为5，把这些数编成一个数组，int max_ef[] = {0,1,2,4,6,8 };，然后因为每次加深深度会拿走一根火柴，如果当前深度为d，最大深度为maxd，g为余下正方形个数，那么\((maxd-d)*max\_ef[n]<g\)时，可以剪枝了。不过也不难看出来这个是一个不怎么好的启发函数。当n为5的时候就已经很慢了，而且没利用到太多当前的状态。
我借鉴的代码：Square Destroyer-POJ 1084 （IDA*）
这哥们好像也是借鉴的其他人的，不知道了。
代码
#include "iostream"
#include "cstdio"
#include "vector"
#include "cstring"
#define MAXN 60
using namespace std;
/*
2
2
0
3
3 12 17 23
1
3
3 12 17 23
*/
// stick[i] 含有火柴i的正方形编号
// square[i] 含有正方形i的火柴编号
vector<int> stick[MAXN],square[MAXN];
int totstick, totsquare,base;
int n,k,ans;
int exi[MAXN], tmp[MAXN];
int max_ef[] = {0,1,2,4,6,8 };
int g() {
int cnt = 0;
for (int i = 1; i <=totsquare; i++)
if (exi[i] >= 0)cnt++;
return cnt;
}
bool dfs(int d, int maxd) {
if ((maxd - d) * max_ef[n] < g()) {
return false;
}
int first=1;
// 找一个没被破坏的正方形
while (exi[first] < 0 && first <= totsquare)first++;
if (first > totsquare) {
ans = min(ans, d);
return true;
}
for (int i = 0; i < square[first].size(); i++) {
// 拿一根火柴
int st = square[first][i];
for (int j = 0; j < stick[st].size(); j++) {
// 把这根火柴能破坏的正方形都破坏掉
exi[stick[st][j]]--;
}
if (dfs(d + 1, maxd))return true;
for (int j = 0; j < stick[st].size(); j++) {
exi[stick[st][j]]++;
}
}
return false;
}
int main() {
int T;
scanf("%d", &T);
while (T--) {
scanf("%d %d", &n,&k);
totsquare = 0, totstick = 2 * n * (n + 1), base = 2*n+1;
for (int i = 1; i < MAXN; i++){
stick[i].clear();
square[i].clear();
}
for (int size = 1; size <= n; size++) {
// i 是每行的第一个火柴
for (int i = 1; (i-1)/base + size<=n ; i+=base) {
for (int j = i; j - i + size <= n; j++) {
// j 是代表每行每个方块顶部的那根火柴
totsquare++;
// top 是大小为size的正方形顶部的所有火柴
for (int top = j; top - j < size; top++) {
// 插入顶部和底部的火柴
square[totsquare].push_back(top);
square[totsquare].push_back(top + size * base);
stick[top].push_back(totsquare);
stick[top+size*base].push_back(totsquare);
}
// l 是大小为size的正方形左边的所有火柴
for (int l = j + n; (l - j - size) / base < size; l += base) {
// 插入左右的火柴
square[totsquare].push_back(l);
square[totsquare].push_back(l + size);
stick[l].push_back(totsquare);
stick[l+size].push_back(totsquare);
}
}
}
}
memset(exi, 0, sizeof(exi));
for (int i = 0; i < k; i++) {
int st; scanf("%d", &st);
for (int j = 0; j < stick[st].size(); j++) {
exi[stick[st][j]]--;
}
totstick--;
}
ans = totstick;
for (int maxd = 0;; maxd++)
if (dfs(0, maxd)) { printf("%d\n", ans); break; }
}
return 0;
}
消防车（Firetruck, ACM/ICPC World Finals 1991, UVa208）
输入一个n（n≤20）个结点的无向图以及某个结点k，按照字典序从小到大顺序输出从结点1到结点k的所有路径，要求结点不能重复经过。
提示：要事先判断结点1是否可以到达结点k，否则会超时。
输入输出
多组输入，每组第一行是k，以下若干行是图中的两个连通节点，以两个零结束。
注意，输出中的空格是一个，不是三个。
Sample Input
6
1 2
1 3
3 4
3 5
4 6
5 6
2 3
2 4
0 0
4
2 3
3 4
5 1
1 6
7 8
8 9
2 5
5 7
3 1
1 8
4 6
6 9
0 0
Sample Output
CASE 1:
1 2 3 4 6
1 2 3 5 6
1 2 4 3 5 6
1 2 4 6
1 3 2 4 6
1 3 4 6
1 3 5 6
There are 7 routes from the firestation to streetcorner 6.
CASE 2:
1 3 2 5 7 8 9 6 4
1 3 4
1 5 2 3 4
1 5 7 8 9 6 4
1 6 4
1 6 9 8 7 5 2 3 4
1 8 7 5 2 3 4
1 8 9 6 4
There are 8 routes from the firestation to streetcorner 4.
思路
太他妈简单了，简单的不能再简单的回溯。。。我都不想做。。。
然后。。。
TLE。。。
我选择自动忽略了刘汝佳说的那句提示：
其实这个提示很有用，如果在20个节点的完全连通图中，每一对节点都能联通，那么从1到k的路径有多少？只考虑经过所有节点的路径，就已经有\(18!\)种排列方式了，其实还有更多，考虑如果路径中没经过2，那么就有\(17!\)种排列方式，数学功底不行，我不数了，反正光是\(18!\)都已经是不可能完成的任务了，累死也搞不完啊。
所以事先用bfs先判断一下连通性，如果根本不连通，就不要试了，无用功。
代码
#include "iostream"
#include "cstdio"
#include "cstring"
#include <queue>
#include <vector>
#include <algorithm>
#define MAX 22
using namespace std;
int target;
vector<int> G[MAX];
int vis[MAX];
int cnt;
bool bfs() {
queue<int> q; q.push(1);
vis[1] = 1;
while (!q.empty()) {
int u = q.front(); q.pop();
if (u == target)return true;
for (int v : G[u]) {
if (vis[v])continue;
vis[v] = 1;
q.push(v);
}
}
return false;
}
/*
cur: 当前选中的节点
*/
void dfs(vector<int> selected){
int last = selected[selected.size() - 1];
if (last == target) {
for(int i:selected){
printf("%d", i);
if (i != last)
printf(" ");
}
printf("\n");
cnt++;
return;
}
for (int adj : G[last]) {
if (vis[adj])continue;
selected.push_back(adj);
vis[adj] = 1;
dfs(selected);
vis[adj] = 0;
selected.pop_back();
}
}
int main() {
int a, b;
int kase = 0;
vector<int> initial = { 1 };
while (scanf("%d", &target) != EOF & target!=0) {
cnt = 0;
for (int i = 0; i < MAX; i++)G[i].clear();
while (scanf("%d %d", &a, &b) != EOF && a != 0 && b != 0) {
G[a].push_back(b);
G[b].push_back(a);
}
printf("CASE %d:\n", ++kase);
memset(vis, 0, sizeof(vis));
if (!bfs()) { printf("There are 0 routes from the firestation to streetcorner %d.\n", target); continue; }
memset(vis, 0, sizeof(vis));
vis[1] = 1;
for (int i = 0; i < MAX; i++)sort(G[i].begin(), G[i].end());
dfs(initial);
printf("There are %d routes from the firestation to streetcorner %d.\n", cnt, target);
}
return 0;
}
黄金图形（Golygons, ACM/ICPC World Finals 1993, UVa225）
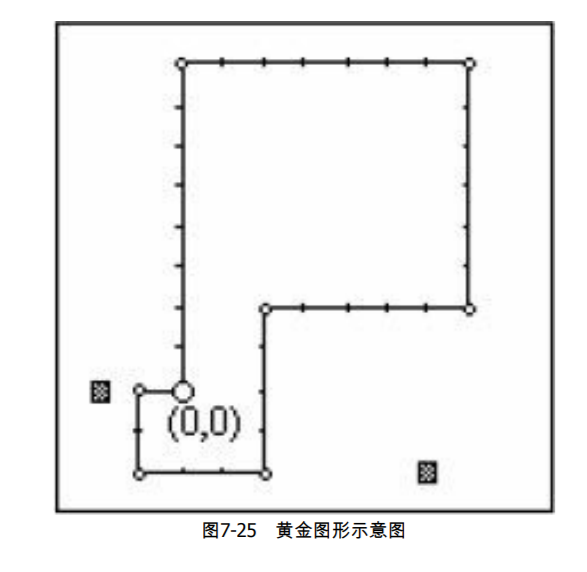
平面上有k个障碍点。从(0,0)点出发，第一次走1个单位，第二次走2个单位，……，第n次走n个单位，恰好回到(0,0)。要求只能沿着东南西北方向走，且每次必须转弯90°（不能沿着同一个方向继续走，也不能后退）。走出的图形可以自交，但不能经过障碍点，先前走过的点也不能经过了(这是题目中没说的，刘汝佳也没说，害我搞了好久）。如图7-25所示。
输入\(n、k（1≤n≤20，0≤k≤50）\)和所有障碍点的坐标，输出所有满足要求的移动序列（用news表示北、东、西、南），按照字典序从小到大排列，最后输出移动序列的总数。
输入输出
输入第一行是输入示例的组数，以下n组的第一行和第二行分别是n和k，下面k行由两个以空格分开的整数组成，即障碍物的xy坐标。
对于每组输入，输出所有能经过n次移动到达起始点的转向方式，并且输出有多少组。
Sample Input
2
8
2
-2 0
6 -2
8
2
2 1
-2 0
Sample Output
wsenenws
Found 1 golygon(s).
Found 0 golygon(s).
思路
相当于枚举所有可能的走法，第一次转弯可以选四个方向，第二次到第n次都只可以选择2个方向，因为只能旋转90度，所以最大的走法就是\(4^1*2^{20-1}=2097152\)，还可以接受。
题目中有一个限制就是之前走过的地方不能走了，这条限制非常适用于dfs，因为dfs每次选择一条路径走到头，这样每次到达一个新点，就能使用一个大小为n的数组来判断之前有没有走过这个点。而用bfs不是每次选择一条路径，而是多条，这样若想完成上面的判断就要维护一个超大的数组，不得行。
所以就用dfs来做，题目中要求按照字典序输出，那就把方向按照字典序编成数组就好了，这样出来的自然就是字典序。
剩下的都是编码问题了。
代码
#include "iostream"
#include "cstdio"
#define MAXK 50
#define MAXN 21
using namespace std;
struct Point {
int x, y, dir;
Point() :x(0), y(0),dir(-1) {}
Point(int x, int y, int dir) : x(x), y(y),dir(dir) {}
bool operator == (const Point& p)const {
return x == p.x && y == p.y;
}
}Route[MAXN + 2] = { Point(0,0,-1) };
char dirs[] = { 'e','n','s','w' };
int dx[] = { 1,0,0,-1 };
int dy[] = { 0,1,-1,0 };
Point blockages[MAXK];
int n, k;
int cnt;
/*
判断这一走是不是穿过了障碍
*/
bool not_through_blockages(const Point& p1, const Point& p2) {
for (int i = 0; i < k; i++) {
// 如果是南北走的，无需考虑x，所以固定住x，只看y
if (p2.dir > 0 && p2.dir < 3 && blockages[i].x == p2.x && blockages[i].y >= min(p1.y, p2.y) && blockages[i].y <= max(p1.y, p2.y))return false;
else if (blockages[i].y == p2.y && blockages[i].x >= min(p1.x, p2.x) && blockages[i].x <= max(p1.x, p2.x))return false;
}
return true;
}
bool is_visited(const Point& p,int cur) {
for (int i = 0; i < cur; i++) {
if (i == 0 && cur == n)continue;
if (Route[i] == p)return true;
}
return false;
}
void show(int cur) {
for (int i = 0; i < cur; i++) {
cout << "(" << Route[i].x << "," << Route[i].y << ")" << " ";
}
cout << endl;
}
bool test(int cur) {
char t[] = "enwneswswnenwse";
int j = 0;
for (int x = 1; x < cur; x++) {
if (dirs[Route[x].dir] != t[j++])return false;
}
return true;
}
/*
cur代表本次dfs计算出的节点需要填充到Route的位置
因为第0个是起点所以始终不会变，初始cur应该是1
*/
void dfs(int cur) {
Point p = Route[cur-1];
if (cur == n + 1 && p.x == 0 && p.y == 0) {
for (int i = 1; i <= n; i++) {
printf("%c", dirs[Route[i].dir]);
}
printf("\n");
cnt++;
}
if (cur == n + 1)return;
//if(test(cur)){
// show(cur);
//}
for (int i = 0; i < 4; i++) {
// 不能走一样方向 不能后退 只能旋转90度
if (i + p.dir == 3 || i == p.dir)continue;
Point new_p(p.x + cur * dx[i], p.y + cur * dy[i], i);
if (!is_visited(new_p,cur) && not_through_blockages(p, new_p)) {
Route[cur] = new_p;
dfs(cur + 1);
}
}
}
int main() {
int T;
scanf("%d", &T);
for (int i = 0; i < T; i++) {
scanf("%d %d", &n, &k);
cnt = 0;
for (int j = 0; j < k; j++) {
scanf("%d %d", &blockages[j].x, &blockages[j].y);
}
dfs(1);
printf("Found %d golygon(s).\n\n", cnt);
}
return 0;
}
切断圆环链（Cutting Chains, ACM/ICPC World Finals 2000, UVa818）
有n（n≤15）个圆环，其中有一些已经扣在了一起。现在需要打开尽量少的圆环，使得所有圆环可以组成一条链（当然，所有打开的圆环最后都要再次闭合）。例如，有5个圆环，1-2, 2-3, 4-5，则需要打开一个圆环，如圆环4，然后用它穿过圆环3和圆环5后再次闭合圆环4，就可以形成一条链：1-2-3-4-5。
输入输出
有多组输入，每组一行，第一个数是n，剩下若干个用空格分开的二元组x y代表xy之间有一条通路。x y若皆为-1，该组输入结束。
当n为0，输入结束。
对于每组输入，输出要形成一条链所需要的最少打开-关闭次数。
Sample Input
5 1 2 2 3 4 5 -1 -1
7 1 2 2 3 3 1 4 5 5 6 6 7 7 4 -1 -1
4 1 2 1 3 1 4 -1 -1
3 1 2 2 3 3 1 -1 -1
3 1 2 2 1 -1 -1
0
Sample Output
Set 1: Minimum links to open is 1
Set 2: Minimum links to open is 2
Set 3: Minimum links to open is 1
Set 4: Minimum links to open is 1
Set 5: Minimum links to open is 1
思路
可能是最近做的题都是什么回溯，IDA星啥的，看到题目愣了半天，觉得是用IDA星解，但这个操作不知道怎么模拟。看了别人的笔记发现了另一种思路，自己实现了一下。还是不能被框架禁锢住思想。
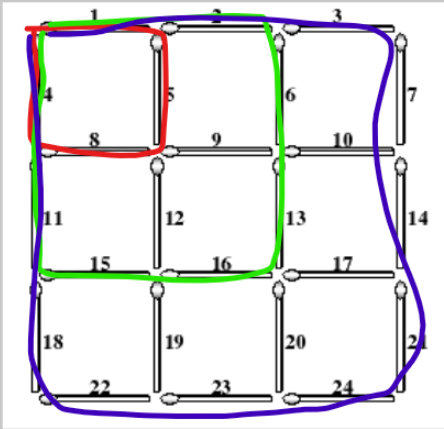
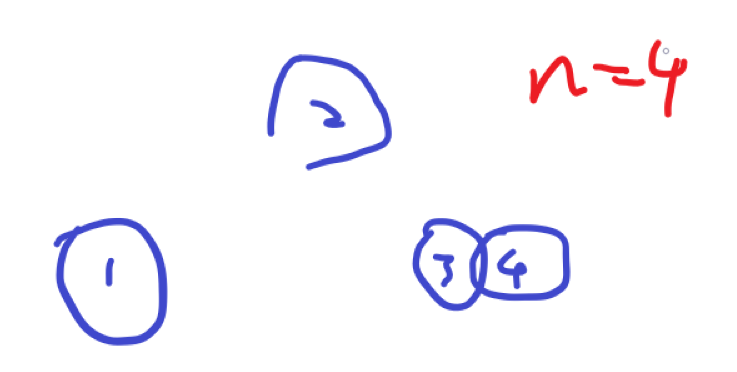
这种思想就是，对于每个圆环，它只有两种状态，打开和关闭。遍历所有打开关闭的状态，判断当前状态中所有打开的圆环能不能把所有圆环穿成一个链，如果能，代表可以用当前打开的圆环次数个打开关闭操作来穿成链，这就是一个答案。取答案中最小的那个即可。比如下图，就可以用2穿1和3后关闭，穿成一个链。
圆环最多15个，那就可以用一个\(2^{15}=32768\)的15位二进制整数来模拟，当第i位为1代表圆环打开，否则代表圆环关闭。
然后看看如何判断能不能用当前打开的圆环把余下的那些穿成一个链。
不难把这些圆环的关系抽象成无向图，圆环i和j相扣，代表i和j间有一条路径。打开的圆环看作已经从图中消失。
- 当抛去打开的圆环后，图中仍有环路出现，则不能穿成链
- 当前连通分量-1如果>打开圆环的个数，则不能穿成链
因为一个打开的圆环可以把两个连通分量连接成一个，仔细考虑下，这和我们小学时候学的植树问题中树和空隙的关系差不多- 如果当前图中有的节点度>2，则不能穿成链
考虑一个图如果退化成链，那么只有旁边两个节点度为1，剩下的都是2，没有超过2的。这不被第一条包含。请考虑只有一层的满三叉树的情况，无环，但根的度为3。
如果满足上面三条，即用当前打开的圆环无法把余下的圆环穿成链，这时我们遍历下一种状态即可。如果三条都不满足，则可以用当前打开的圆环数量次打开关闭操作连成链，记录答案。
代码
#include "iostream"
#include "cstring"
#include "cstdio"
#define MAXN 16
using namespace std;
int n;
int state;
int G[MAXN][MAXN];
int vis[MAXN];
int deg[MAXN]; // deg计算度
int ans,CC; // ans答案 CC记录连通分量个数
/*
计算二进制数state中有几个1
*/
int open_cnt() {
int cnt = 0;
int max_state = 1 << n;
for (int i = 1; i <= max_state; i = i << 1) {
if (i & state)cnt++;
}
return cnt;
}
bool is_opened(int v) {
return state & (1 << v - 1);
}
/*
dfs从一个节点开始，递归查询是否有环
查询到环后不退出，保证该节点所在的连通分量中所有节点都被访问过
*/
bool dfs(int prev,int cur) {
vis[cur] = 1;
if (is_opened(cur))return false;
bool has_circle = false;
for (int v = 1; v <= n; v++) {
if ((G[cur][v] || G[v][cur]) && !is_opened(v)) {
deg[cur]++;
if (!vis[v]) {
bool tmp = dfs(cur,v);
if (!has_circle) has_circle = tmp; // 如果已经检测到有环，那么后面的检测影响不到有环的事实
}
else if(v!=prev) has_circle = true;
}
}
return has_circle;
}
/*
此方法返回是否存在环
当检测到环时，不能退出。该函数要保证找环的同时计算出连通分量个数和每个结点的度
*/
bool has_circle() {
memset(vis, 0, sizeof(vis));
memset(deg, 0, sizeof(deg));
int has = false;
CC = 0;
for (int i = 1; i <= n; i++) {
if (!vis[i] && !is_opened(i)) {
if(dfs(0,i)) has = true;
CC++;
}
}
return has;
}
bool has_deg_bigger_than_2() {
for (int i = 1; i <= n; i++)if (deg[i] > 2)return true;
return false;
}
void solve() {
int max_state = 1 << n;
for (; state <= max_state; state++) {
int oc = open_cnt();
if (has_circle() || has_deg_bigger_than_2() || CC - 1 > oc)continue;
ans = min(ans, oc);
}
}
int main() {
int kase = 0;
while (scanf("%d", & n) != EOF && n!=0) {
state = 0; ans = MAXN;
memset(G, 0, sizeof(G));
int a, b;
while (scanf("%d %d", &a, &b) != EOF && (a != -1 || b != -1)) {
G[a][b] = 1; G[b][a] = 1;
}
solve();
printf("Set %d: Minimum links to open is %d\n", ++kase, ans);
}
return 0;
}
流水线调度（Pipeline Scheduling, UVa690）
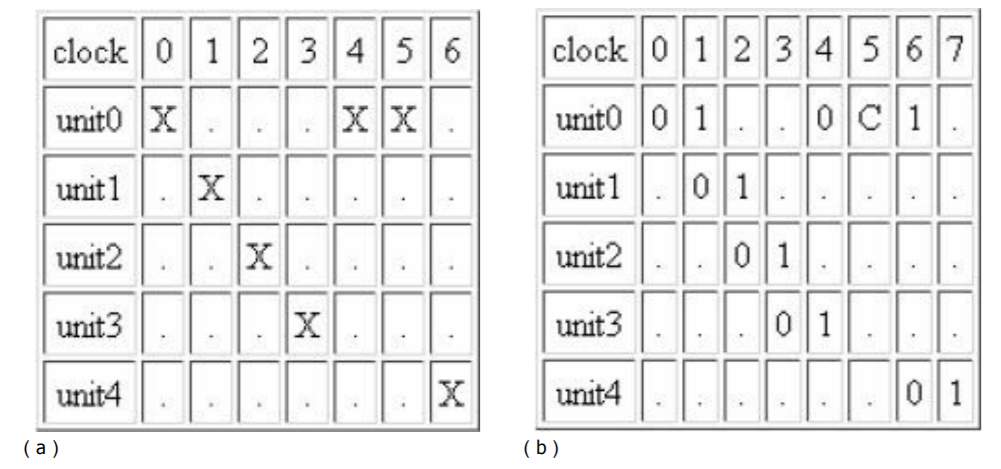
你有一台包含5个工作单元的计算机，还有10个完全相同的程序需要执行。每个程序需要\(n（n<20）\)个时间片来执行，可以用一个5行n列的保留表（reservation table）来表示，其中每行代表一个工作单元（unit0～unit4），每列代表一个时间片，行i列j的字符为X表示“在程序执行的第j个时间片中需要工作单元i”。例如，如图7-28（a）所示就是一张保留表，其中程序在执行的第0, 1, 2, ……个时间片中分别需要unit0, unit1, unit2……同一个工作单元不能同时执行多个程序，因此若两个程序分别从时间片0和1开始执行，则在时间片5时会发生冲突（两个程序都想使用unit0），如图7-28（b）所示。输入一个5行n（n<20）列的保留表，输出所有10个程序执行完毕所需的最少时间。例如，对于图7-28（a）的保留表，执行完10个程序最少需要34个时间片。
输入输出
Sample Input
7
X...XX.
.X.....
..X....
...X...
......X
0
Sample Output
34
思路
这个题目贼不好理解，可能是我操作系统什么的课学的不好吧。我就是因为搞错了题目的意思浪费了一天。
其实题目中有一个限制，就是一个任务一旦开始，就必须从时钟0一直执行到时钟n-1，不能停下。当一个任务开始后，它就会在n个时钟周期内结束，其中每一个时钟周期，新的任务都可能开始（前提是不会产生工作单元的冲突）。并且，这些工作单元不能停下，也就是说这五个工作单元里最少也要有一个任务。
代码是照人家抄的。
思路是，使用五个二进制数作为当前五个工作单元哪里是需要独占的。比如上面的示例可以用如下几个二进制数表示
这里和输入是反的。对应位为1证明这个位置可能被占用。还有，为了方便，我统称这五个二进制数为图。其实它不是图。
0110001
0000010
0000100
0001000
1000000
这是初始情况下一个任务进入，可能会在某一个时间片独占某一个工作单元。
当走过k个时钟周期，这个图就相当于每个二进制数都右移了k次，因为之前的已经执行完了，不会再发生冲突。假如k=3，那么这些二进制数是
0000110
0000000
0000000
0000001
0001000
每次走过一个时钟周期，都可能有一个新任务开始执行，如果这个新任务开始执行，对于它来说，可能产生竞争的工作单元就是输入数据那张图。每次新增一个任务，我们把输入数据和之前已有的图进行或操作就是新的可能发生冲突的工作单元。比如第一个时钟周期任务1开始，过了3个时钟周期，到第4个时钟周期，第2个任务开始，就相当于上面那个图和输入图做或操作，得到如下图
0110111
0000100
0001000
1001000
这是新的可能发生冲突的图，对于后面的任务如果想进来后不间断执行，就必须挑选一个好的时间点进入。
如何判断是否会发生冲突？
因为新生任务可能发生冲突的地方就是输入图，那么只需要将输入图和当前可能发生竞争的图进行与操作（每一行，也就是每一个工作单元），如果有大于1的，就证明会发生竞争，这时新生任务就不能进入，就得再等几个时钟周期。
所以该题目就可以先把第一个任务加进去，然后dfs，每次选择等待1~n个时钟周期，如果其中的某个时钟周期加入新任务不会发生冲突，就加入，再次dfs，每次dfs加一个新任务，当深度为10即代表任务已经全部加入。
代码
#include "iostream"
#include "cstring"
#include "cstdio"
#define MAXU 5
#define MAXT 10
using namespace std;
int start[MAXU];
int wait_time[MAXT],ans,n,cnt;
bool judge(int* s, int k) {
for (int i = 0; i < MAXU; i++)
if ((s[i] >> k) & start[i])return false;
return true;
}
void init() {
memset(start, 0, sizeof(start));
memset(wait_time, 0, sizeof(wait_time));
ans = n * 10; cnt = 0;
for (int i = 0; i < MAXU; i++) {
getchar();
for (int j = 0; j < n; j++) if (getchar() == 'X') start[i] |= 1 << j;
}
for (int i = 1; i <= n; i++)
if (judge(start, i)) wait_time[cnt++] = i;
}
void dfs(int d,int *cur,int sum) {
if (sum + (MAXT - d) * wait_time[0] > ans) return;
if (d == MAXT) {
ans = min(ans, sum); return;
}
for (int i = 0; i < cnt; i++) {
if (judge(cur, wait_time[i])) {
int next[MAXU];
for (int j = 0; j < MAXU; j++) next[j] = (cur[j] >> wait_time[i]) | start[j];
dfs(d + 1, next, sum + wait_time[i]);
}
}
}
int main() {
while (scanf("%d", &n),n) {
init();
dfs(1, start,n);
printf("%d\n", ans);
}
return 0;
}
重叠的正方形（Overlapping Squares, Xia'an 2006, UVa12113）
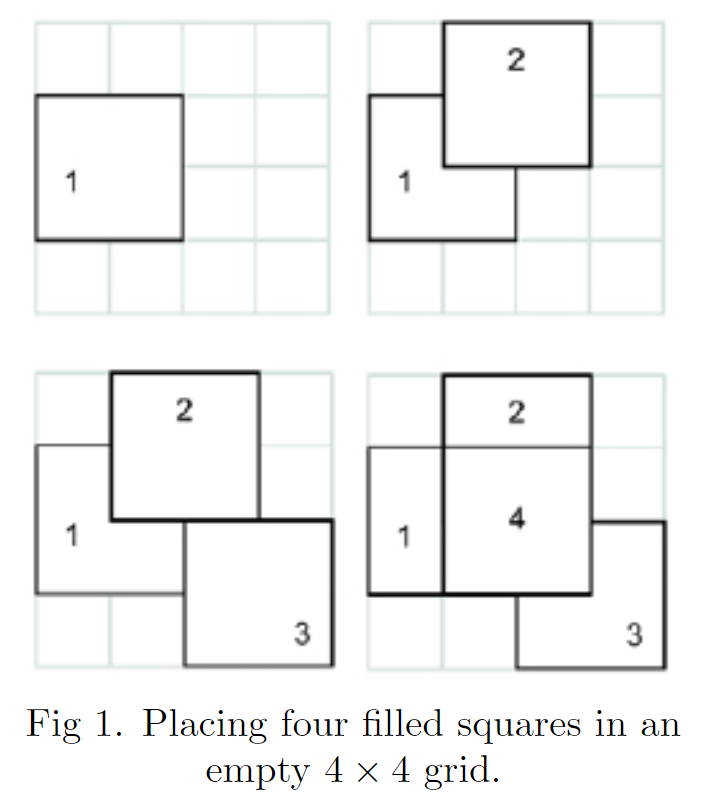
在第一张图中，我们在一个\(4\times 4\)的大正方形网格中放了一个\(2\times 2\)的正方形1，在第二张图中又放了个正方形2，它把第一个正方形的一些线给挡住了。在第三第四张图中又放置了两个正方形。显然，它们也挡住了之前的一些线。
随着正方形越来越多，得到的图形会越来越复杂。
编写一个程序，判定能否通过摆放1到6个\(2\times 2\)正方形得到题目中要求的图形。
输入输出
包含多组输入，每组五行，每行包含九个字符，使用这个代表\(4\times 4\)网格。_代表一个横向边，|代表一个纵向边，空格代表啥也没有。
每行以#结束。
输入以0结束。
对于每组输入，输出它的编号，以及使用1到6个\(2\times 2\)正方形能否得到对应图形。
Sample Input
#
_ _ _ #
| |_ _| #
|_| | #
|_ _| #
#
_ _ #
| | #
|_ _| #
#
_ _ _ _ #
|_|_|_|_|#
|_|_|_|_|#
|_|_|_|_|#
|_|_|_|_|#
_ _ #
_| |_ #
| |_ _| |#
|_| |_|#
|_ _|_|#
_ _ _ _ #
| |#
| |#
| |#
|_ _ _ _|#
_ #
|_| #
#
#
#
_ #
|_| _ #
|_|#
#
#
_ #
|_|_ _ _ #
|_|_|_|#
| | #
|_| #
0
Sample Output
Case 1: Yes
Case 2: Yes
Case 3: No
Case 4: Yes
Case 5: No
Case 6: No
Case 7: No
Case 8: No
思路
看到这个输入都傻了。不知道怎么接。
仔细想想不是特别难。
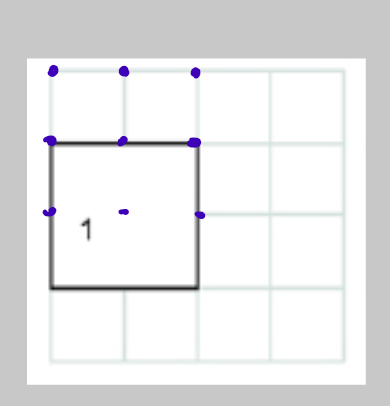
由于题目中最多使用6个\(2\times 2\)正方形，网格固定是\(4\times 4\)，所以正方形只能被放置在九个位置，下图是正方形左上角能放置的位置。
然后也不用特意处理这个输入，直接用一个叫target的\(5\times 9\)的字符数组直接接进来就可以了。
题目相当于让我们在白纸上按一定顺序把6张正方形放置在那九个位置，并且每一次放置都看看是不是已经等于target了，如果是就不用再试了。
所以这就是dfs+回溯，每次选择一个正方形并选择一个点，选过的点不能选择了，就是这样。
代码
我也不知道为啥我把它转成int了。。。。脑袋抽了。。。
#include "iostream"
#include "cstring"
#include "cstdio"
#define SPACE 0
#define AXIS 1
#define UNDERLINE -1
using namespace std;
int target[5][9];
int initial[5][9];
int vis[9];
int dy[] = { 0,2,4 };
int dx[] = { 0,1,2 };
int kase = 1;
void put_rect(int g[5][9], int x,int y) {
g[x][y + 1] = g[x][y + 3] = g[x + 2][y + 1] = g[x + 2][y + 3] = UNDERLINE;
g[x + 1][y] = g[x + 1][y + 4] = g[x + 2][y] = g[x + 2][y + 4] = AXIS;
g[x + 2][y + 2] = g[x + 1][y + 1] = g[x + 1][y + 2] = g[x + 1][y + 3] = SPACE;
}
bool build(){
memset(vis, 0, sizeof(vis));
char tmp[5][11];
for (int i = 0; i < 5; i++) {
cin.getline(tmp[i],11);
if (tmp[i][0] == '0')return false;
}
for (int i = 0; i < 5; i++) {
for (int j = 0; j < 9; j++) {
if (tmp[i][j] == ' ')target[i][j] = SPACE;
else if (tmp[i][j] == '|')target[i][j] = AXIS;
else target[i][j] = UNDERLINE;
}
}
return true;
}
bool dfs(int d, int cur[][9]) {
if (d >= 0 && d <= 6) {
if (memcmp(target, cur, sizeof(target)) == 0) {
return true;
}
if (d == 6) {
return false;
}
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
int x = dx[i] , y = dy[j],id = i*3+j;
if (!vis[id]) {
int new_g[5][9];
memcpy(new_g, cur, sizeof(new_g));
put_rect(new_g, x, y);
vis[id] = 1;
if (dfs(d + 1, new_g))return true;
vis[id] = 0;
}
}
}
}
return false;
}
int main() {
memset(initial,SPACE, sizeof(initial));
while (build()) {
if (dfs(0, initial)) {
cout << "Case " << kase++ << ": Yes" << endl;
}
else {
cout << "Case " << kase++ << ": No" << endl;
}
}
return 0;
}
看网上还有好多使用二进制枚举来做的，肯定会更快，但是此题因为输入规模小，不像上一题，使用这个就能过了，就不折腾了。如果要折腾的话会更新。
卧槽写了这么多，编辑器都有点卡了，我再开另一篇文章吧，就写到这~~~
