递推——高级计数技术
递推
都是来自《离散数学及其应用》第八章中的例题和习题。
递推是指将一个看似复杂，难以求解的问题一步步的转换成小问题，最后到达一个（或若干个）基本解，这些基本解很好想出来(也有的是人为规定的)，然后再依赖这些基本解一步一步反向求解最初的大问题的过程。
举一个最简单和常见的例子，斐波那契数列，这个数列的每一项等于前面两项之和。如下：
\(\{1,1,2,3,5,8,13...\}\)
如果让你直接求斐波那契数列的第100个数\(f(100)\)，很难直接想出来，但是我们可以通过找到如下的递推关系：\(f(n) = f(n-1) + f(n-2)\)，并且确定基本解\(f(1)=1，f(2)=1\)(因为递推关系只依赖前面两项，所以只求出基本的两项即可)，之后就可以求出\(f(3)\)，再用\(f(2)+f(3)\)求\(f(4)\)，最后求解到\(f(100)\)。
很多问题可以找到递推关系，所以这个工具很常用，比如解决具有重叠子问题的递推关系的算法叫“动态规划”，它出现在很多面试题和算法竞赛当中 。
递推关系确实很难想，但想出来的感觉也确实很爽。
下面是题~爽吧
汉诺塔
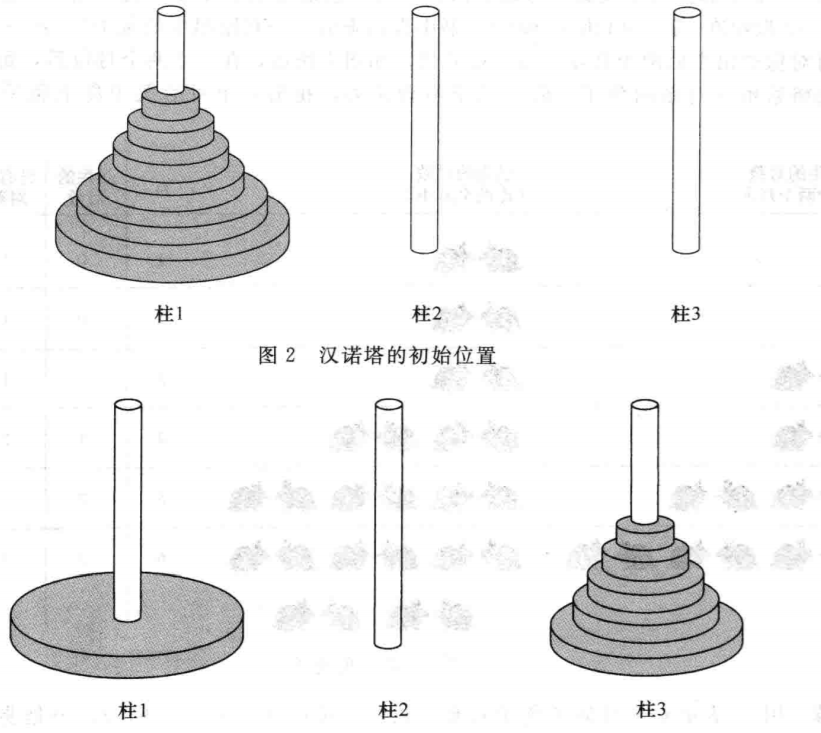
有三根柱子和n个直径不同的圆形盘子，开始时这些盘子按照直径大小插在第一根柱子上，我们想把这些盘子按原顺序移动到第二根柱子上，并且移动的过程中直径更大的不能落在直径更小的盘子上。\(H_n\)为完成操作需要的移动次数，求\(H_n\)。
对于n个盘子，我们可以使用\(H_{n-1}\)次移动把这些盘子移动到柱子3上，再使用一次移动把最大的盘子移动到柱子2，再花\(H_{n-1}\)次把柱子3的盘子移动到柱子2。
\(H_n=2H_{n-1}+1\)
二进制串
对于不含两个连续0的n位二进制位串的个数\(a_n\)。
- 可以把n位这样的二进制串分成两类，以0结尾的和以1结尾的\(a_n=以0结尾的个数+以1结尾的个数\)
- 对于以1结尾的，它的个数为\(a_{n-1}\)，因为它只是在\(n-1\)位题目中合法的二进制串后加了个1
- 对于以0结尾的，它的个数为\(a_{n-2}\)，因为不能存在两个连续0，所以它的最后两位肯定是10，所以是\(a_{n-2}\)个
- 所以\(a_n=a_{n-1}+a_{n-2}\)
- 初始条件，\(a_1=2\)（0,1)，\(a_2=3\)（01,10,11）
编码字的枚举
如果一个数字串包含偶数个0，我们认为它是合法的，否则不合法。\(a_n\)为n位数字串中的合法数字个数，求\(a_n\)。
- 把第n个数字分为10种情况
- 若该数字是1~9则不改变原来串的合法性，这时有\(9\times a_{n-1}\)个合法串
- 若该数字是0，则会改变原来串的合法性，原来不合法的（奇数个零）的那些串变为合法的，这时有\(10^{n-1}-a_{n-1}\)个合法串
- \(a_n=8\times a_{n-1}+10^{n-1}\)
- \(a_1=9\)
能加多少括号
\(C_n\)为表达式\(x_0\times x_1\times x_2 \times ... \times x_n\)中能插入括号的个数，所有的括号插入必须代表不同的乘法顺序。
列一张表
| \(C_n\) | 所有可能性 | 括号加法个数 |
|---|---|---|
| \(C_0\) | \((x_0)\) | 1 |
| \(C_1\) | \((x_0\times x_1)\) | 1 |
| \(C_2\) | \((x_0\times x_1) \times x_2\) \(x_0\times (x_1\times x_2)\) |
2 |
| \(C_3\) | \(((x_0\times x_1)\times x_2)\times x_3\) \((x_0\times (x_1\times x_2))\times x_3\) \((x_0\times x_1)\times (x_2\times x_3)\) \(x_0\times ((x_1 \times x_2)\times (x_3))\) \(x_0\times (x_1\times (x_2\times x_3))\) |
5 |
可以发现（这他妈谁能发现），从\(C_2\)开始，每一个式子都有一个乘号在外面，没被括号包裹。以它为界，左边的和右边的都可以看成是之前的子问题。比如拿\(C_3\)中的第一行和第二行来说，裸漏在外面的乘号是第三个，第三个乘号左边就是\(C_2\)，乘号右边就是\(C_0\)，所以\(C_3\)中乘号在第三个位置的时候有\(C_2\times C_0=2\times 1=2\)种括号加法。
所以对于每一个乘号位置，它把\(x_k\)和\(x_{k+1}\)分开，它能为整体贡献\(C_k\times C_{n-k-1}\)个括号加法。
所以\(C_n=\sum_{k=0}^{n-1}C_k\times C_{n-k-1}\)
集合排列
找到一个关于有n个元素的集合的排列数的递推关系\(T(n)\)。
- 当集合只有一个元素的时候，只有一种排列。\(T(1)=1\)
- 当我们选中第n个元素的时候，前面\(n-1\)个元素已经确定，它们有\(T(n-1)\)个排列。
- 第n个元素可以插到前面\(n-1\)个元素排列的任意一个位置，这个位置有n个，所以\(T(n)=nT(n-1)\)
自动售货机
一台自动售货机只接受1美元硬币、1美元纸币以及5美元纸币。
找到放n美元到这台售货机的方式数的递推关系\(T(n)\)，确定初始条件，求买一个10美元的商品有多少种付款方式。
- 当我们选中5美元纸币的时候，剩余要付的金额是\(n-5\)，对应的付款方式为\(T(n-5)\)
- 当我们选中1美元硬币的时候，付款方式为\(T(n-1)\)
- 选中1美元纸币的时候，付款方式为\(T(n-1)\)
- 综上，\(T(n)=T(n-5)+2T(n-1)\)
- 递推式中依赖n往前第5项，所以至少要找出\(T(0)到T(4)\)，这些都用不了五元，所以只能选两种一元。
- \(T(0)=1（不付款），T(1) = 2^1=2，T(2)=2^2=4，T(3)=2^3 = 8，T(4) = 2^4 =16\)
- 使用递推关系式求\(T(10)\)即可，略。
比索
一个国家使用的货币叫做“比索”，硬币面值有1、2、5、10，纸币价值有5、10、20、50、100。如考虑硬币和纸币的次序，求付n比索时的方式数的递推关系\(T(n)\)。
- 和上一题差不多，直接给出递推式
- \(T(n) = T(n-1)+T(n-2)+2T(n-5)+2T(n-10)+T(n-20)+T(n-50)+T(n-100)\)
想要实现一个算法，需要至少算出T(0)~T(99)。不过当n很小时，可以忽略一些根本用不到的面额，比如n=10时，只需要考虑1、2、5、10这些面值的纸币和硬币。也就是说上面的递推式加和中的后3项可以去掉。
二进制串2
求与包含2个连续0的n位二进制串的个数有关的递推式\(T(n)\)与初始条件。
上面有一道差不多的题目，那个是求不包含两个连续0的。这个需要考虑的情况更多一些。
- 当二进制串包含两个连续0时，我们称它是合法的。
- 当第n位选1时，不改变前面\(n-1\)位的合法性，合法串个数为\(T(n-1)\)。
- 当第n位选0时，有两种情况，第一种是第\(n-1\)位是0，这时前面的\(n-2\)个二进制串组成的任何串都是合法的，所以有\(2^{n-2}\)个组合。
- 当第n位选0并且第\(n-1\)位是1时，不改变前面\(n-2\)位的合法性，所以是\(T(n-2)\)
- 综上，\(T(n)=T(n-1)+T(n-2)+2^{n-2}\)。
过桥费
一个汽车司机只用5美分和10美分硬币付过桥费，每次向收费机投一个硬币，求付n美分时的付款方式数的递推关系\(T(n)\)。
根据前面的经验，此题非常简单，我们可以很轻易地写出递推关系式，\(T(n) = T(n-5) + T(n-10)\)
不过不难发现，5元和10元只能组合成5n美元，也就是说司机只能付5的倍数的过桥费，对于\(T(5n+i),i\in \{1,2,3,4\}\)，可能的付款方式都是0。如果我们按照动态规划的思想，对于\(T(n)\)把所有\(T(k),k<n\)都计算出来作为一个数组存储的话，会有很多冗余的数据。就像下面。
这里T(0) = 1，就是当需要支付0美分时，唯一的办法就是什么都不付
{1,0,0,0,0,1,0,0,0,0,2,0,0,0,...}
这里面有很多0，它们又没啥卵用。
所以可以以其他方式定义\(T(n)\)。
\(T(n)\)为想支付5n时的支付方式数，这样\(T(n) = T(n-1)+T(n-2)\)（选一个五美分和选一个十美分）。
这样，可以这样写算法
function solve(int n){
// 如果不是5n，直接返回0
if(n%5!=0)return 0
T = {1,1} // T(0)和T(1)
for i=2 to n/5{
T[i] = T[i-1]+T[i-2]
}
return T[n/5]
}
分割平面
如果\(R_n\)是一个平面被n条直线分割后划分出的区域个数。这些直线没有互相平行的，没有三条直线交于一点，找出\(R_n\)的递推关系式。
- 每次添加一条合乎题目要求的直线，必会且只会与\(n-1\)条原来就存在的直线相交
- 这原来的\(n-1\)条直线划分了\(n\)个区域
- 新增的直线把这\(n\)个区域分割成\(2n\)个区域
- 新增了\(2n-n=n\)个区域
- 所以\(R_n=R_{n-1}+n\)
- 初始条件 \(R_0=1\)
可能不好想象，自己画个图吧。
原书答案中给的解释大概是，想象新增一条直线时，会交于原来的\((n-1)\)个直线，想象从直线的一端出发，每经过一个交点，会把原来的一个平面分割成两个，当经过\(n-1\)个交点后，最后还有一个，所以新增了n个。
二进制串3
求出具有包含偶数个0的n位二进制串个数有关的递推关系\(T(n)\)。
- 当第n位为1时，有\(T(n-1)\)个这样的二进制串
- 当第n位为0时，有包含奇数个0的\(n-1\)位二进制串个
- 包含奇数个0的n位二进制串个数为\(2^n-T(n)\)
- 所以当第n位为0时，有\(2^{n-1}-T(n-1)\)个包含偶数个0的n位二进制串
- \(T(n) = T(n-1)+2^{n-1}-T(n-1) = 2^{n-1}\)
多米诺骨牌
找到与使用\(1\times 2\)的多米诺骨牌完全覆盖\(2\times n\)棋盘的方式数的递推关系式\(T(n)\)。(提示：考虑棋盘右上角横放和竖放两种情况)
- 当右上角的牌竖放时，牌大小\(2\times 1\)，此时的方式数相当于在\(2\times (n-1)\)大小的棋盘上的摆放方式数，显然是\(T(n-1)\)种
- 当右上角的牌横放时，牌大小\(1\times 2\)，此时若想填满棋盘，它的下面也必须是一个横放的牌，这时的方式数相当于在\(2\times (n-2)\)大小的棋盘上的摆放方式数，为\(T(n-2)\)种
- \(T(n) = T(n-1) + T(n-2)，T(1)=1，T(2)=2\)，就是右移了一位的斐波那契数列。
地砖
用地砖铺一块人行横道，地砖是红色、绿色或灰色的，如果没有两块红砖相邻且同色的地砖是不加区别的，找出与用n块砖铺一条路的方式数的递推关系式\(T(n)\)
- 当对一个本来就没有两块相邻红砖的\(n-1\)块砖组成的人行横道铺砖，下一块砖选择绿色和灰色时，不可能产生连续两块红色，所以分别有\(T(n-1)\)种方式，就是\(2T(n-1)\)。
- 当铺红砖时，想保证这条路没有两块相邻红砖，上一块砖就得是绿的或者灰的，这时分别有\(T(n-2)\)种方式，就是\(2T(n-2)\)
- \(T(n) = T(n-1) + T(n-2)\)
此题可以看作组成长度为n的不包含两个连续0的3进制串有多少种方式。
斐波那契反向证明
请证明\(f_n=5f_{n-4}+3f_{n-5}\)
请使用上述结论证明\(f_{5n}\)可以被5整除
我们使用数学归纳法。
当n为1，\(f_{5\times 1} = 5\)可以被5整除。假设前提条件成立，则\(f_{5(n+1)}=5f_{5_n+1}+3f_{5n}\)，这个式子能被5整除，所以成立。
