修改天平——UVa 12166

修改天平（Equilibrium Mobile, NWERC 2008, UVa12166）

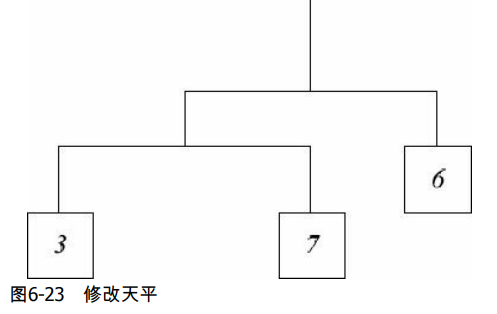
给一个深度不超过16的二叉树，代表一个天平。每根杆都悬挂在中间，每个秤砣的重量
已知。至少修改多少个秤砣的重量才能让天平平衡？如图6-23所示，把7改成3即可。

输入

示例第一行为整数n，它代表有多少组测试示例。

以下的n行每一行是一组单独的测试示例。每组测试实例是一个表达式，表示天平所代表的二叉树。

表达式的语法规则如下

< expr >::=< weight >| "["< expr >","< expr >"]"

如上图对应的测试示例是：[[3,7],6]

输出

对于每组测试示例，输出使天平平衡，最小要修改的砝码数。

测试示例

Sample Input
3
[[3,7],6]
40
[[2,3],[4,5]]


Sample Output
1
0
3

思路

搞了一下午，没啥思路。输入都处理不好。

所以这题挺好的，对于只有叶子节点有值的那种树，提供了一个输入的模板，还有对于解决这种题目提供了一个有意思的思路。据说这个思路在竞赛中挺常用的。

基本思路就是，我们既然要修改一个砝码使天平平衡，那肯定就要有一个砝码是参考砝码，然后按照它来改。对于一个砝码，如果指定它是参考砝码了，那整个天平的总重量就能确定了，就是\(weight\times 2^{depth}\)。depth是这个砝码当前在树中的深度。

还是看这个图

如果使用3作为参考砝码，那么整个天平的重量是\(3\times 2^2=12\)，需要修改砝码7为3。

如果使用7作为参考砝码，那么整个天平的重量是\(7\times 2^2 = 28\)，需要修改砝码3为7，6为14。

如果使用6作为参考砝码，那么整个天平的重量是\(6\times 2^1 = 12\)，需要修改砝码7为3。

我们发现三次参考砝码的选择中，有两次得到的天平总重量都是12，也就是说，这两个砝码如果修改其中一个，另一个就不用改。那么我们把使用每一个砝码得到的天平总重记录起来，找到其中出现次数最多的那个，然后我们用砝码数减去它就是最少修改砝码数了。

代码

#include "iostream"
#include "cstdio"
#include  "cstring"
#include "map"
#define LL long long

using namespace std;

char line[1500000];

map<LL, int> ID;
int sum;
void dfs(int l,int r,int d) {
    if (line[l] == '[') {
        int level=0;
        for (int i = l+1; i <= r; i++) {
            if (line[i] == '[') level++;
            else if (line[i] == ']') level--;
            if (level == 0 && line[i] == ',') {
                dfs(l + 1, i - 1, d + 1);
                dfs(i + 1, r-1, d + 1);
            }
        }
    }
    else {
        int w;
        sscanf(line+l,"%d", &w);
        ID[(LL)w * (1 << d)]++;
        sum++;
    }
}

int main() {
    int n;
    scanf("%d", &n);
	getchar();
    for(int i=0;i<n;i++){
        ID.clear(); sum = 0;
        scanf("%s", line);
        dfs(0,strlen(line)-1,0);
        map<LL, int>::iterator it;
        int max=0;
        for (it = ID.begin(); it != ID.end(); it++) 
            max = it->second > max ? it->second : max;
        printf("%d\n", sum - max);
    }
    return 0;
}

参考

随缘&不屈——UVA12166-Equilibrium Mobile