自组合——UVa 1572

给定n种正方形，每种正方形有4条边，每条边有2个字符构成，包含以下两种模式：

第一个为A-Z的大写字母，第二个为+/-，如A+或Z-
00
当两条边的第一个字符相同，而第二个字符相反时，两边可相连，00不可与任何边相连。

现假设每种正方形无限供应，并且可以随意旋转和翻转，问是否存在无限拼接图像？

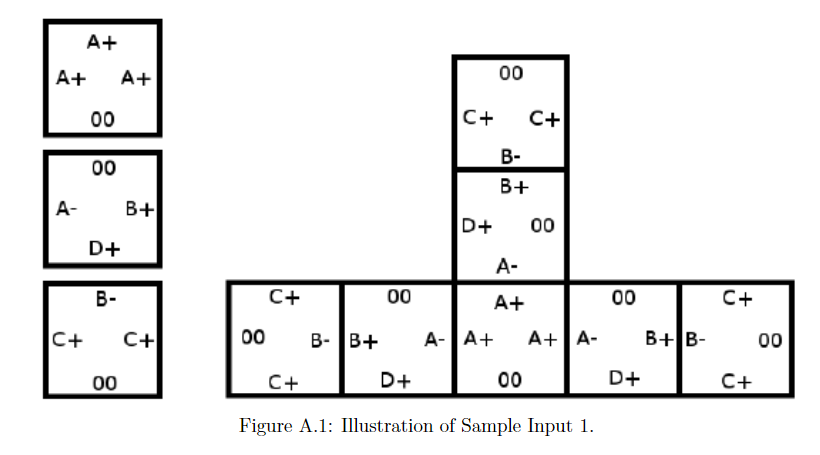
下图是这些正方形的一个拼接方式。

包含若干组输入，每组输入的第一行是数字n，代表该组数据有几个正方形，然后是对应的正方形的四条边上的字符，对于每组输入，如果它不能无限拼接，输出bounded，否则输出unbounded。

Sample Input

3
A+00A+A+ 00B+D+A- B-C+00C+
1
K+K-Q+Q-

Sample Output

bounded
unbounded

题解

看了别人的才有思路。

用图来解是没啥问题了，关键是怎么构造这个图。这个不好想。

这里的办法是用每个可能出现的字符，A+ A- ... Z+ Z-当作图的节点，这样只有52个节点，00不算因为它无法和任何节点连通。

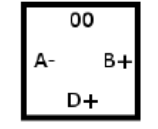
然后关键是怎么建立连接关系。就拿下面这个正方形来说。

比如，这个节点，对于A-这条边。因为正方形可以随意反转和旋转，所以它在哪条边不重要。其他正方形如果想连接到这个正方形，就需要与A+相连，所以要建立B+、D+到A+的单向连接。对于其他两个节点也一样。

现在问题转换成了图，所以问能不能无限构造就相当于问这个有向图中有没有环。

#include "iostream"
#include "cstdio"
#include "cstring"
#define MAX 52
#define CONN 1
#define NOCONN 0
#define VISITING 1
#define UNVISITED 0
#define VISITED -1

using namespace std;

int g[MAX][MAX];
int vis[MAX];
char rect[9];

int to_id(char c,char s) {
    int offset = s == '+' ? 0 : 26;
    return c - 'A' + offset;
}
int to_other_id(char c, char s) {
    int offset = s == '+' ? 26 : 0;
    return c - 'A' + offset;
}
char first(int i) { return rect[i * 2]; }
char second(int i) { return rect[i * 2 + 1]; }
void handle_rect() {
    for (int i = 0; i < 4; i++) {
        if (first(i) == '0')continue;
        for (int j = 0; j < 4; j++) {
            if (first(j) == '0')continue;
            if (i != j) {
                int fid = to_other_id(first(i), second(i));
                int tid = to_id(first(j), second(j));
                g[fid][tid] = CONN;
            }
        }
    }
}
bool dfs(int i){
    vis[i] = VISITING;
    for (int j = 0; j < MAX; j++) {
        if (g[i][j]==CONN) {
            if (vis[j] == VISITING) { 
                return false; 
            }
            else if (vis[j] == UNVISITED && !dfs(j)) return false;
        }
    }
    vis[i] = VISITED;
    return true;
}
bool assert_bounded() {
    for (int i = 0; i < MAX; i++) 
        if (vis[i] == UNVISITED && !dfs(i)) return false;
    return true;
}
int main() {
    int n;
    while (scanf("%d", &n) != EOF) {
        memset(g, NOCONN, sizeof(g));
        memset(vis, UNVISITED, sizeof(vis));
        for (int i = 0; i < n; i++) {
			scanf("%s", rect);
            handle_rect();
        }
		bool b = assert_bounded();
        if (!b) {
            printf("unbounded\n");
        }
        else {
            printf("bounded\n");
        }
    }
    return 0;
}

参考

• wyjoutstanding 例题6-19 UVA1572 Self-Assembly