ACM_HDU_2045_不容易系列之(3)—— LELE的RPG难题

Problem Description

人称“AC女之杀手”的超级偶像LELE最近忽然玩起了深沉，这可急坏了众多“Cole”（LELE的粉丝,即"可乐"）,经过多方打探，某资深Cole终于知道了原因，原来，LELE最近研究起了著名的RPG难题:

有排成一行的ｎ个方格，用红(Red)、粉(Pink)、绿(Green)三色涂每个格子，每格涂一色，要求任何相邻的方格不能同色，且首尾两格也不同色．求全部的满足要求的涂法.

以上就是著名的RPG难题.

如果你是Cole,我想你一定会想尽办法帮助LELE解决这个问题的;如果不是,看在众多漂亮的痛不欲生的Cole女的面子上,你也不会袖手旁观吧?

Input

输入数据包含多个测试实例,每个测试实例占一行,由一个整数N组成，(0<n<=50)。

Output

对于每个测试实例，请输出全部的满足要求的涂法，每个实例的输出占一行。

Sample Input

1 2

**Sample Output

3 6

Author

lcy

Solution

动态规划。

定义dp[n]为有n个方格情况下所有满足要求的涂法。

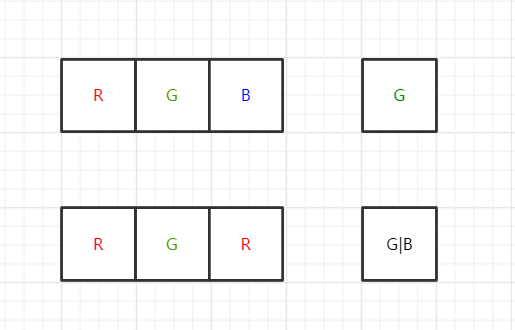
对于dp[n]，我们看作是向n-1个格子组成的序列中插入一个新格子，这n-1个格子可以本身就满足要求(相邻异色，首尾异色)，这时我们新加入的格子就只能选择一个颜色，所以选法就是dp[n-1]。这n-1个格子也可以不满足要求，因为我们的第n个格子马上要成为尾格子，只要第n个格子和首格子不同，整体还是满足要求的。这时选法是dp[n-2]*2个，见下图。

所以，状态转移方程就是

dp[n] = dp[n-1] + dp[n-2] * 2

初始条件是第一第二第三个格子。

dp[1] = 3
dp[2] = 6 // 3 * 2
dp[3] = 6 // 因为首尾异色，并且前两个必是异色的，所以还是6

C++实现

#include "iostream"
#include "cstdio"

using namespace std;

long long dp[51];

int main() {
    int n,size=3;
	dp[1] = 3; dp[2] = 6; dp[3] = 6;
    while (scanf("%d", &n) != EOF) {
        for (; size < n;) 
            dp[++size] = dp[size - 1] + dp[size - 2] * 2;
        printf("%lld\n", dp[n]);
    }
    return 0;
}