平衡查找树(2-3树和红黑树)

在一般情况下，二叉树的查找效率很高，但在极个别情况下会出问题，这依赖于输入数据的顺序。

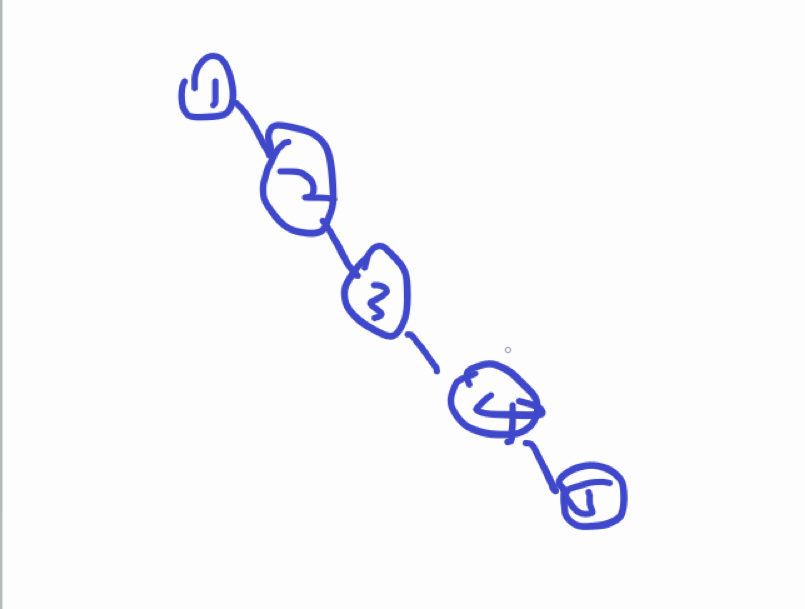
如果我们给BTree<Char,Int>(代表键是字符值是整数的二叉树)插入这样一串数据：[1,2,3,4,5]，那我们得到的二叉树就是这样的。

二叉树退化成了链表，而我们查找一个数据的时间复杂度也退化成了\(O(n)\)。

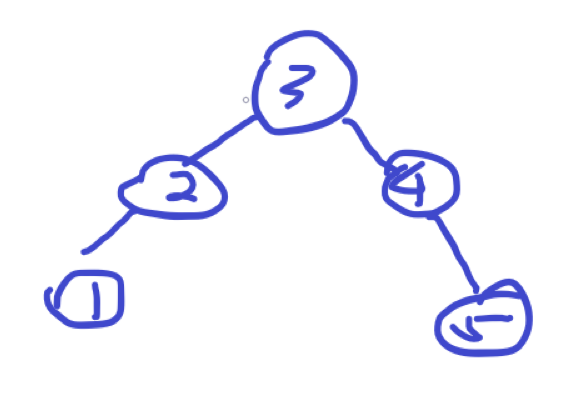
平衡查找树用于解决这个问题，平衡查找树中会做一些操作，使得插入的数据在树中分布的很平衡，树的高度以对数级别上升，这样的话查找起来就非常快了。如上图的数据在平衡查找树里可能会被插入成这样

2-3树

2-3树通过把节点分成2节点和3节点，并通过向上分裂的操作保证搜索树的平衡性。

2节点

2节点指有左右两个子节点的节点。同时此节点中有一个数据元素。和二叉搜索树中的节点一样，左子节点中的数据比当前节点的数据小。右子节点中的数据比当前节点的数据大。

3节点

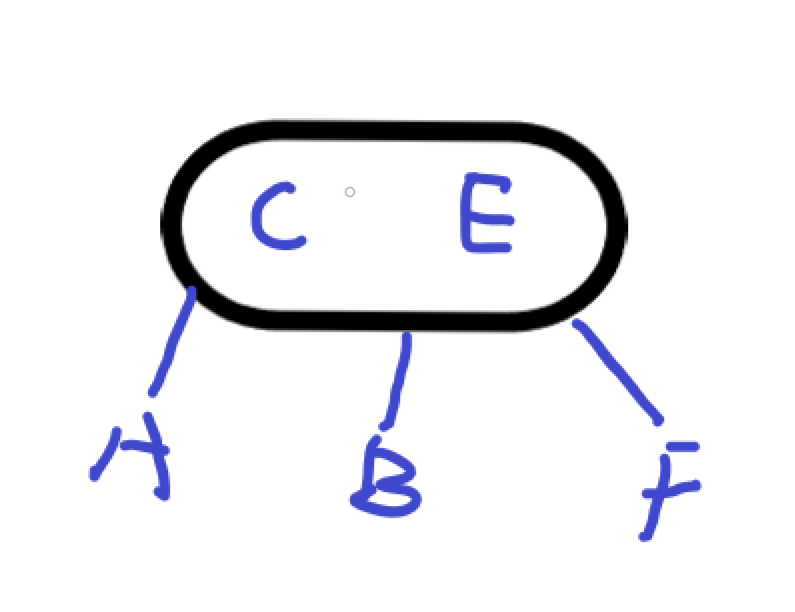
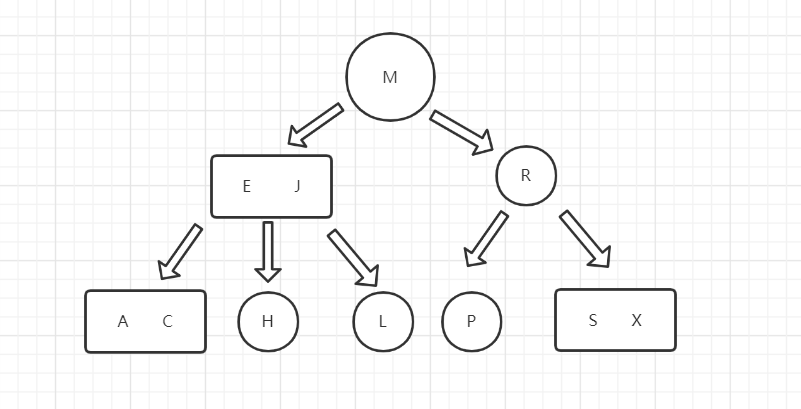
3节点指有左中右三个子节点的节点。同时节点中存在两个数据元素。左侧元素比右侧元素小，左侧子节点中的元素比左侧元素小，中间子节点的元素大于左侧子节点的元素小于右侧子节点的元素，右侧子节点中的元素大于右侧元素。

示例

插入

如果想造出一颗平衡搜索树，肯定要在插入和删除的时机做一些手脚，才能保证树中的元素分布平衡。

对于2-3树，我们需要考虑如下两种情况：

1. 要插入的节点位置的父节点是2节点
2. 要插入的节点位置的父节点是3节点

对于第一个情况，我们又可以细分为两种情况

1. 待插入的节点比父节点小
2. 待插入的节点比父节点大

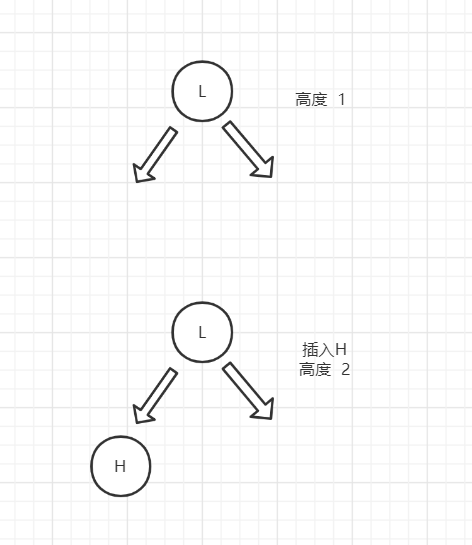
因为我们要保持整棵树的平衡性，所以我们不能直接像二叉查找树一样，把节点直接挂在2节点下，这有时会增加树的高度。

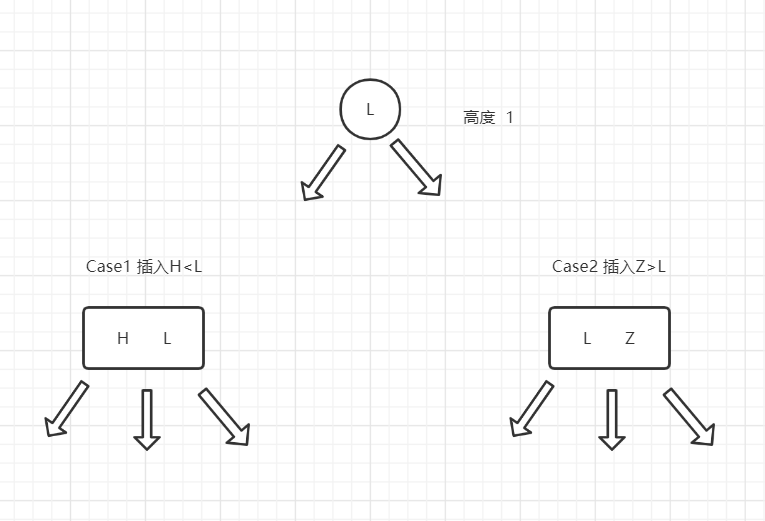
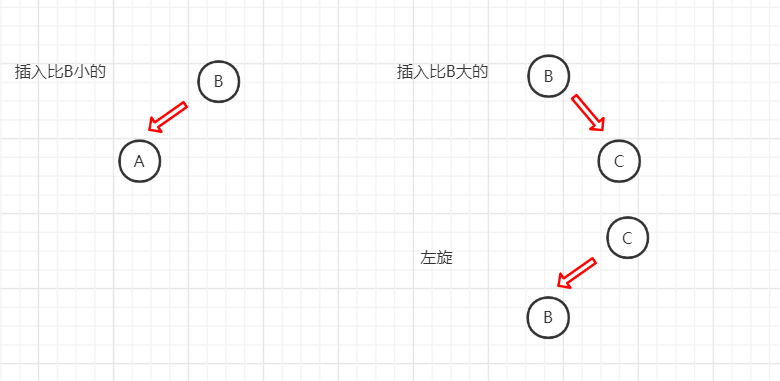
如果我们不想改变树的高度，那么我们就可以把待插入节点插入到父节点当中去，使父节点变为一个3节点，但3节点有元素大小的顺序规定，所以我们不能随便插入。分如下两种情况：

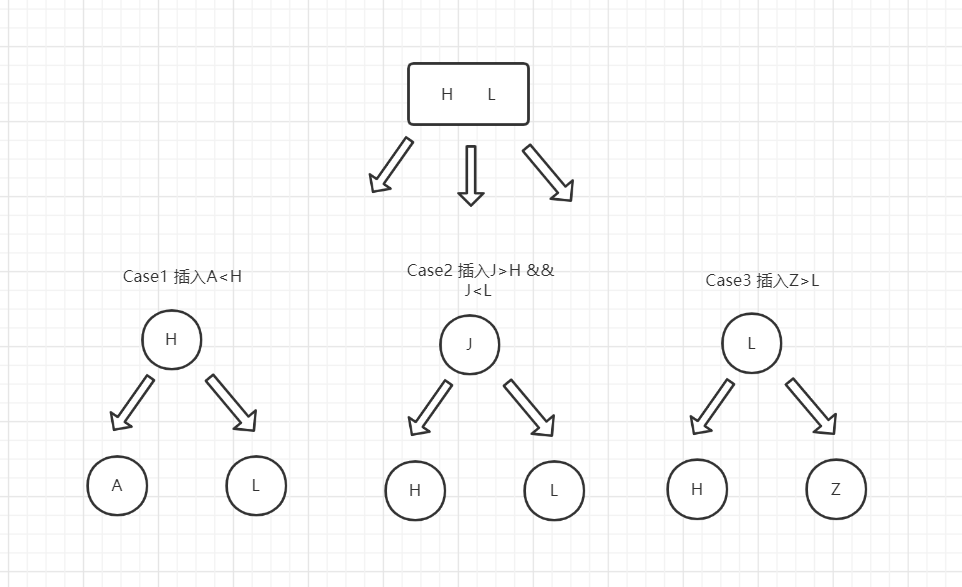
当第二种情况发生的时候，也就是父节点是一个3节点，那就稍微有些麻烦，我们不能把待插节点简单的加到父结点中，因为这会变成一个4节点，2-3树中没有四节点。这时候我们可以采取向上分裂的办法。当然这又得分三种情况。

1. 待插节点小于3节点左侧元素
2. 待插节点大于3节点左侧元素小于3节点右侧元素
3. 待插节点大于3节点右侧元素

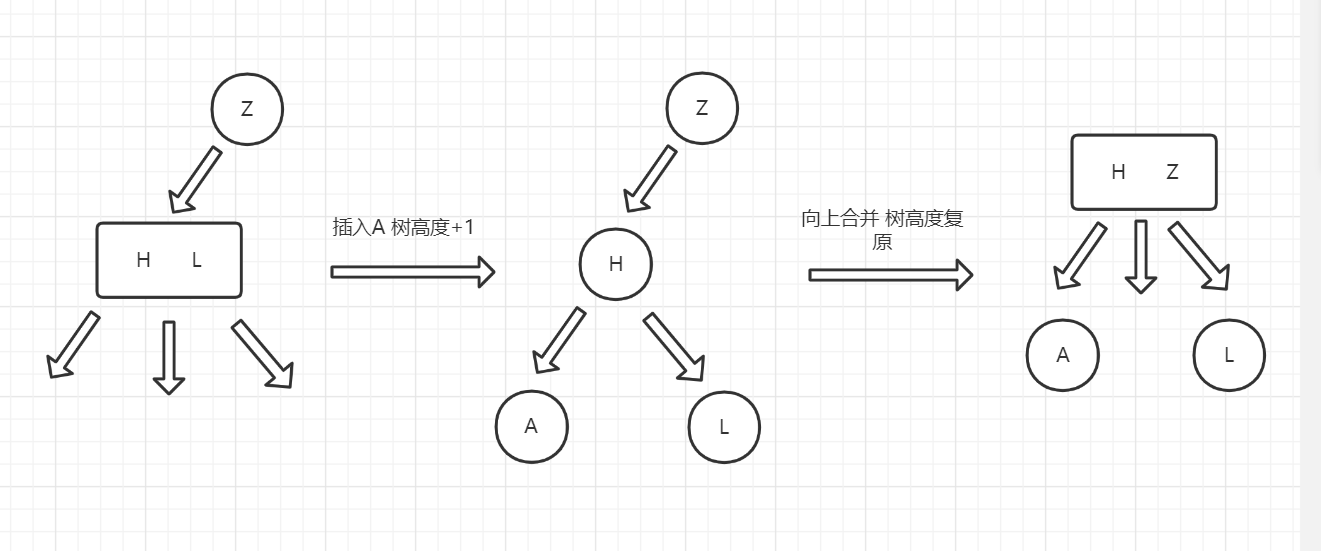
如上图，我们把一个4节点（3节点加1待插节点）按三种情况分裂成了三个2节点。但是可以看到树的高度增加了，按理说是破坏了平衡性。其实不是，我们用递归的方式，把4节点中提出去的那个根节点（Case1中的H，Case2中的J，Case3中的L）当作新的待插入节点，再去判断它的父节点，如果它的父节点是2节点，就按照上面的规则把它归并到父节点中成为一个3节点，如果父节点是3节点就继续分裂，一直到树根。

到了树根后，树的整体高度+1。

局部变化

讲了这么多，主要的还是要理解，2-3查找树的所有插入操作都是局部操作，归并和分裂操作使得插入一个节点不影响整体的平衡性。

总结

2-3搜索树是由下向上生长的，相比于二叉搜索树，2-3树能在任何情况下都保证最坏的查找情况在对数级别。当然，这要从插入和删除操作的时间复杂度和实现复杂性上来做牺牲。

2-3查找树确实是一个不错的想法，但是实现起来非常不方便，要处理的情况非常多，写出来代码也会很丑。所以下面来看一个基于二叉树的2-3树等价替代品——红黑树。

红黑树

红黑树通过设置链接颜色来模拟2-3树。推荐把红黑树的所有操作与2-3树的操作做对比，你会发现实际上就是一个等价代换。

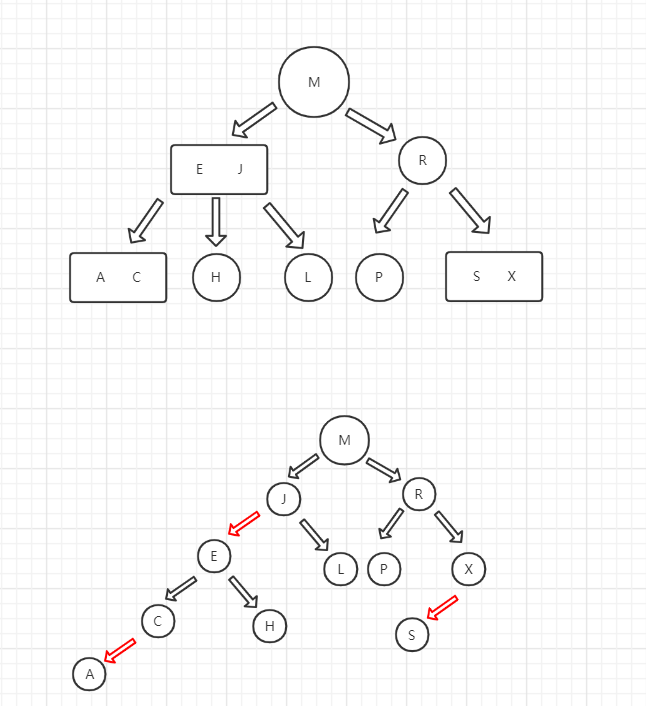
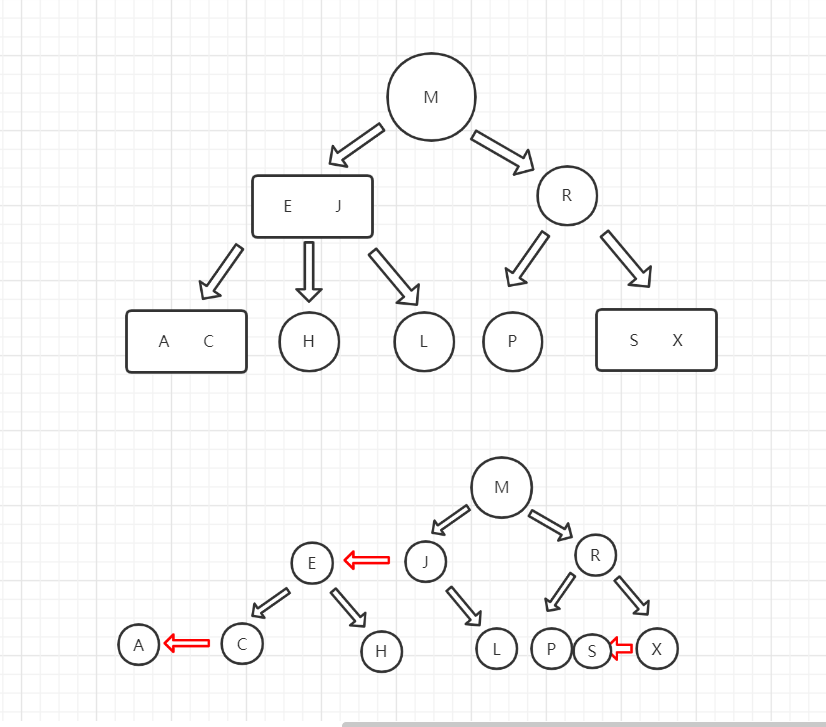
红黑树用红链接代表3节点结构，用黑链接代表正常父子关系。下面是一个2-3树和红黑树的等价代换。

如果把红链接横过来，就更形象了。

为了让逻辑清淅，规定红黑树有如下性质：

1. 红链接只能是指向左子节点的链接
2. 没有任何一个节点同时和两条红链接相连
3. 完美黑色平衡，所有空链接到根节点的距离相同

旋转

使用旋转操作保证上面的三条性质。

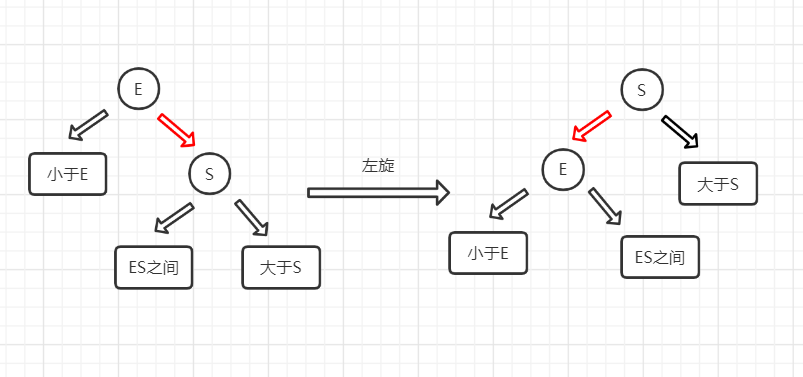
规定两个操作，分别是左旋和右旋。先看左旋，很形象。

伪代码

//h就是上图中的E节点
Node rotateLeft(Node h){
    Node x = h.right;
    h.right = x.left;
    x.left = h;
    //!!!!!!color描述的是父节点到该节点的颜色!!!!!!
    x.color = h.color;
    h.color = RED;
    return x;
}

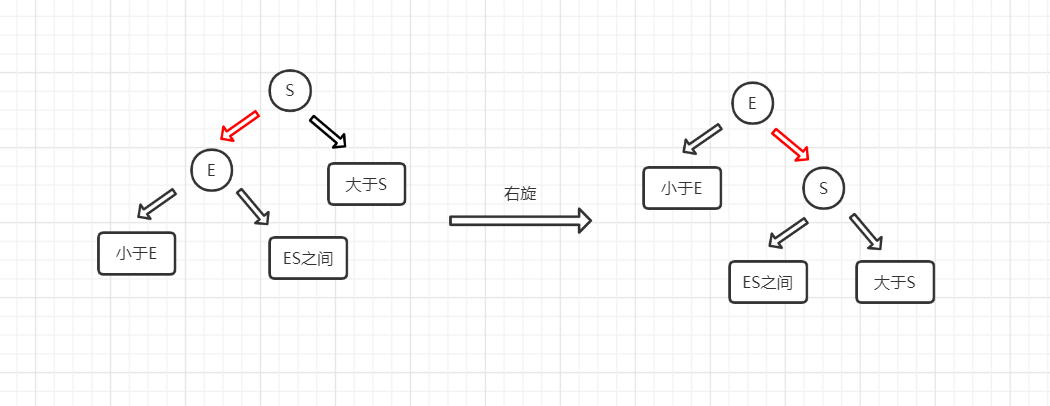
右旋操作则相反

伪代码

Node rotateRight(Node h){
    Node x = h.left;
    h.left = x.right;
    x.right = h;
    x.color = h.color;
    h.color = RED;
    return x;
}

插入

左旋右旋的操作看起来迷迷糊糊的不知道是在干啥，但是把它应用到插入算法中，立马就知道它的功效了。

在这之前还要说一嘴，虽然上面的代码里已经说过了。h.color代表的是h的父节点到h之间的链接的颜色。我们说h是红的，意思是它到它的父节点之间链接是红色的。

插入算法也有两种情况

1. 待插入节点的父节点颜色是黑的
2. 待插入节点的父节点颜色是红的

和2-3树比较着看，这两条其实和2-3树的情况完全相同，第一个代表父节点是个2节点，第二个代表父节点是个3节点。

对于父节点是黑节点(2节点)的插入，如果待插节点比父节点小，则直接插入到左子节点并设置成红色，类比2-3树就是把待插节点和父节点合并成3节点并且把待插节点放到3节点的左侧。如果待插节点比父节点大，则也是直接插入到右节点，同时也设置成红色，但是红黑树不允许右红节点，所以进行一次左旋操作就好了。

这里注意，我们讨论红节点的时候把它和其父节点看作2-3树中的3节点，也就是把红链接相连的两个节点看成一个3节点

对于父节点是红节点(3节点)的插入，我们又要分成三种情况：

1. 待插入节点比父节点中的两个键小
2. 待插入节点介于父节点的两个键之间
3. 待插入节点比父节点的两个键大

和2-3树一样，这里需要一个向上递归的分裂操作。

先规定一下，我们插入的新节点默认都是红色的。

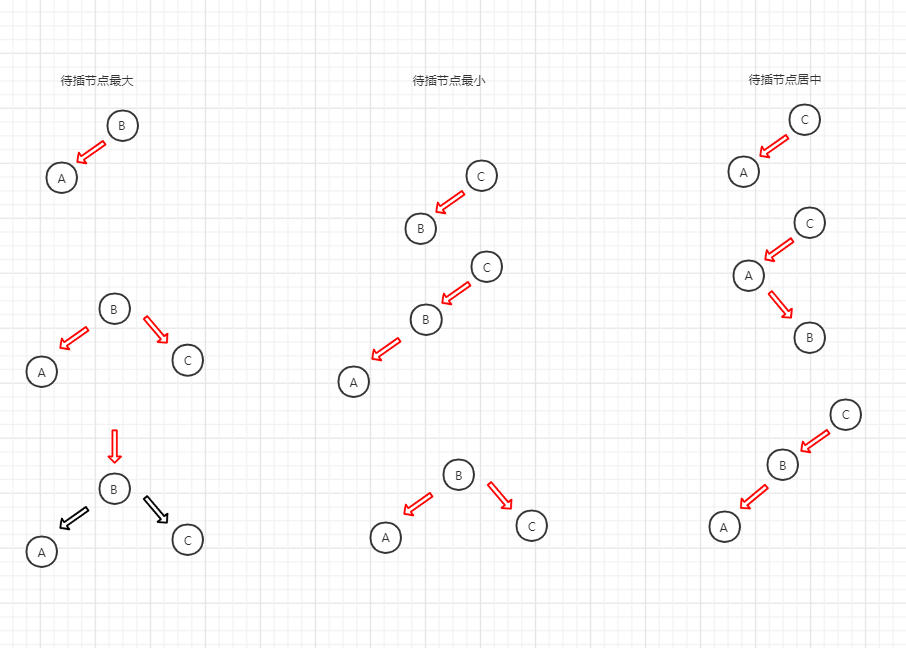
最简单的情况就是待插入节点比父节点的两个键大，这时只需插入到父节点的最右侧，然后就成了下图中第一种情况，左右都是红节点，这代表2-3树中的一个4节点，这时我们要向上分裂，把4节点分裂成三个2节点，并让2节点递归向上合并，在红黑树中我们只需要把这两个红节点改成黑色的并把中间的那个节点改成红节点即可。

第二种情况就是待插入节点最小，这时我们就插入到父节点左侧，并且对父节点(图中的B)进行一个右旋操作，就可以得到和第一种情况一样的情况，再按照第一种情况进行分裂和向上合并的处理即可。

第三种情况就是待插入节点在父节点的两个元素之间，小于左边的，大于右边的，这个时候只需要把待插入节点接到两者之间，在红黑树中就是上层节点的右节点上，然后左旋上层节点即可得到第二种情况，按第二种情况处理即可。

C++实现

我写不出这代码，这完全是把《算法 第四版》中的代码翻译成C++了。很精妙~

#ifndef _RB_TREE_H
#define _RB_TREE_H
#define ERROR 0
#define SUCCESSED 1
#define RED 2
#define BLACK 3

typedef int Color;

typedef struct RBTreeNode {
	struct RBTreeNode * left, * right;
	char key;
	int val;
	Color color;
}RBTreeNode;

typedef struct RBTree {
	RBTreeNode* root;
}RBTree;


RBTree* createRBTree();
int insertToRBTree(RBTree *tree,char key,int val);
int deleteFromRBTree(RBTree* tree, char key);
int containsKey(RBTree* tree, char key);

#endif

#include "stdio.h"
#include "stdlib.h"
#include "string.h"
#include "rb_tree.h"

#define LEFT 1
#define RIGHT 2

RBTreeNode* _createRBTreeNode(char key,int val,Color color) {
	RBTreeNode* node = (RBTreeNode*)malloc(sizeof(RBTreeNode));
	node->color = color;
	node->key = key;
	node->val = val;
	node->right = NULL;
	node->left = NULL;
	return node;
}
RBTree* createRBTree() {
	RBTree* tree = (RBTree*)malloc(sizeof(RBTree));
	tree->root = NULL;
	return tree;
}

RBTreeNode* rotateLeft(RBTreeNode* h) {
	RBTreeNode* x = h->right;
	h->right = x->left;
	x->left = h;
	x->color = h->color;
	h->color = RED;
	return x;
}

RBTreeNode* rotateRight(RBTreeNode* h) {
	RBTreeNode* x = h->left;
	h->left = x->right;
	x->right = h;
	x->color = h->color;
	h->color = RED;
	return x;
}


void flipColors(RBTreeNode* h) {
	h->left->color = BLACK;
	h->right->color = BLACK;
	h->color = RED;
}

int isRed(RBTreeNode* h) {
	return h != NULL && h->color == RED;
}

RBTreeNode* _insertToRBTree(RBTreeNode* h, char key, int val) {
	if (h == NULL) 
		return _createRBTreeNode(key, val, RED);
	if (h->key > key) h->left = _insertToRBTree(h->left, key, val);
	else if (h->key < key) h->right = _insertToRBTree(h->right, key, val);
	else h->val = val;

	
	if (isRed(h->right) && !isRed(h->left)) h = rotateLeft(h);
	if (isRed(h->left) && isRed(h->left->left)) h = rotateRight(h);
	if (isRed(h->left) && isRed(h->right)) flipColors(h);
	return h;
}

int insertToRBTree(RBTree* tree, char key, int val) {
	tree->root = _insertToRBTree(tree->root,key, val);
	tree->root->color = BLACK;
	return SUCCESSED;
}