基于梯度下降法的线性回归
线性回归就是用直线拟合一批数据,例如下面是一组二维数据,线性回归就是拟合出一条最优的直线使得这些数据点和这条直线之间的误差最小。
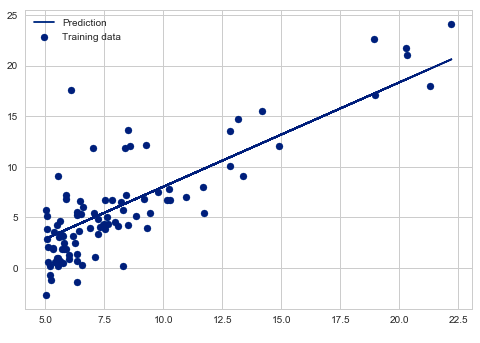
线性代数中有一个最小二乘法也是用来解决这个问题的,在统计学里也非常常用,它和梯度下降法各有优劣,但是这篇笔记主要介绍梯度下降法,所以不讨论最小二乘。
其实从名字不难看出,梯度下降主要用的是一些微积分的知识,这个算法很简单易懂。在学习它之前,先来看一些概念。
样本数据
样本数据是一个二维矩阵,长这样
| \(x_1\) | \(x_2\) | ... | \(x_n\) | \(y\) |
|---|---|---|---|---|
| 2000 | 4450 | ... | 2400 | 1035 |
| 1590 | 3200 | ... | 3459 | 1094 |
如上即一个n维空间的样本,\(x_1,x_2,...,x_n\)称作输入数据,\(y\)是输出数据,或者说是目标值,我们要做的是从样本数据中找出一条最优的直线,能尽量拟合这些数据,然后做到输入一个n维空间中的点,输出一个预测值y
符号约定
假设函数
假设函数\(h_\theta(x)\)就是我们要拟合的那条直线,\(\theta\)是就是我们用来控制这条直线的一些参数,我们用二维数据举例,假设函数的形式就是
多维空间也类似
大部分参考资料中为了标准化,在原数据中加了一列\(x_0=1\),然后假设方程就是
这样便于用矩阵表示,方便计算机编程
我们的目的就是寻找一组\(\theta=[\theta_0\ \theta_1\ \theta_2\ ...\ \theta_n]^T\),让我们的直线与数据更加贴合。
代价函数
代价函数表示的是原始数据和我们拟合出来的直线之间的方差和,例如下图就是在二维空间的一组数据\([1\ 2\ 3]\),和我们拟合出来的直线\(y=0.5x\),这里\(\theta_0=0,\theta_1=0.5\)
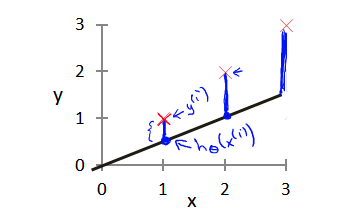
这几个蓝色的线段即我们当前的直线和样本数据的差值,我们要计算的是方差,所以应该是
我们给出一个具有m条样本的标准的代价函数计算公式
前面的1/2m我也不知道具体有啥含义,不过无所谓,都差不多。知道的欢迎告诉我哈~
我们的目的就是让这个代价函数最小化。
我们还是用上面的二维空间的例子,用图像的形式来理解代价函数

这里我们为了更加直观,就让\(\theta_0\)一直为0把,反正这个例子中最终拟合出的直线\(y=x\)中\(\theta_0\)就是0。
这里我们看右侧的图像,右侧是当\(\theta_1\)选择不同的值的时候,代价函数的大小。可能不准确,就是那个意思。当\(\theta_1\)为1时,取得最优解,代价函数为0,也就是当我们用这个\(\theta_1\)作为假设函数的参数时,得出来的直线是完美贴合样本数据的。
当然,现实的例子中几乎不可能完美,如果都能完美,那就成了解m个n维方程构成的方程组问题了,那还用鸡毛梯度下降?直接算不香嘛?
梯度下降
嘶,你可能已经看出点啥了,从上面的代价函数我们可以看出来,这不就是求一个二次函数最小值嘛。那我们学过的数学知识有哪些可以用来求最小值??——求导!!对于一元函数,求导,多元函数就是求偏导。导数求出来就可以求极值了。
所以你也能猜到,梯度下降只能找到局部的最优解,对于全局最优解,它可能无能为力。这就是我们课本上学的用导数求解函数极值问题,求出来的只是局部的最大最小值,并不是整个函数上的。
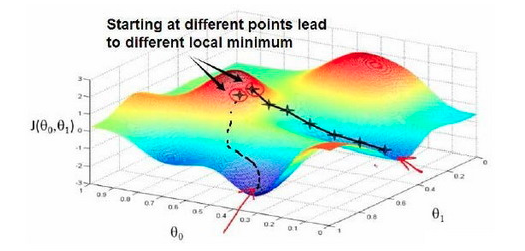
就像上面,这是一个多元假设函数,我们从两个点出发,可能会得到不同的结果,不过他们都是局部的最优解。
具体算法如下,还是先用只有\(\theta_1\)的版本
这里的\(:=\)代表计算机语言中的赋值操作,就是用等式后面的值更新等式前面的变量。而\(a=b\)则代表了一个断言,意思是a与b等价。这个生涩的公式摆在这可能很难以理解,看图。
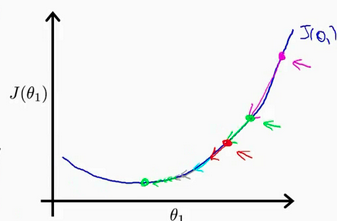
假设我们最初的\(\theta_1\)代入假设函数中得到的误差在图中粉色的点,每一次运行梯度下降算法\(\theta_1\)都会减小\(a\frac{dJ(\theta_1)}{d\theta_1}\),我们可以看到现在误差函数所在的点函数是增的,所以导数也是正的,减去一个正数,误差自然就会减小,到了绿色的点,我们称作下降。而我们可以看到每一次下降,都比上一次缓慢,这是因为越接近最优解的位置,函数的斜率就会越缓,导数也就越小,最优解那点的导数为0,所以到了最优解,就会收敛于那里,不再下降。
式子中的a是一个下降速率。
现在给出n维空间的梯度下降算法公式
过拟合与欠拟合
下降速率a的选择很考究,a如果选大了就会出现过拟合现象,就是下降的过程中越过了最优点,然后误差会反向上升。下降速率过小就会欠拟合,无法或者很难到达最优解。
关于程序
正确的梯度下降算法是同步更新参数的,就是如下所示

\(\theta\)在最后同步更新
Python代码
我没去仔细的学过Pandas,Numpy和什么TensorFlow那些库,唉,有时候真的感觉自己好拉垮,什么都不是,废物一个。
我随便手写了一个代码,先放一张拟合出来的效果图
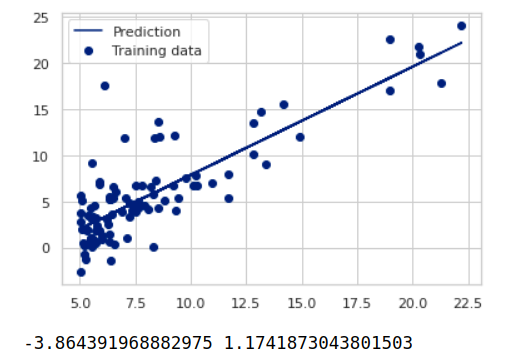
妈的一个没上过高中的孩子在那里对着电脑搞了几个小时。。。。
然后我放出代码,写的有点乱,我也没精力改了,写完这篇我就要去躺着了,我尽量把注释写上吧。还有就是大佬就不要喷了,不过指正我这里面出现的错误可以~~
import numpy as np
import pandas as pd
import seaborn as sns
sns.set(context="notebook", style="whitegrid", palette="dark")
import matplotlib.pyplot as plt
# 损失函数
def J(t0,t1):
error = 0
m = 0
for index,row in datas.iterrows():
m = m + 1
h_y = t0+t1*row['x']
real_y = row['y']
error = error + (h_y-real_y)**2
return 2/m*error
# 梯度下降
def gradient_descent():
# 学习速率
a = 0.01
# 参数0 为什么初始是-5,因为我试了几次,在这个点进行梯度下降得到的局部最优解比较好
cur_t0 = -5
# 参数1
cur_t1 = -5
# 误差 我最开始把它定义的大一点,不过这个定义成多少都无所谓 只要小于期望即可
error = 10000
# 期望 就是你希望误差到多小后停止拟合
expectation = 18
# 当前误差满足期望,也就是说足够小的时候退出循环
while error > expectation:
# 导数项中关于参数0的求和变量
sum_0 = 0
# 导数项中关于参数1的求和变量
sum_1 = 0
# 记录下数据条数,pandas应该有直接获取的API不过我不知道
m = 0
# 遍历数据,计算求偏导数项中的求和项
for index,row in datas.iterrows():
sum_0 = sum_0 + (cur_t0+cur_t1*row['x']-row['y'])
sum_1 = sum_0 * row['x']
m = m + 1
# 计算两个参数下降后的值,a后面的就是偏导数项
temp0 = cur_t0 - a * (1/m) * sum_0
temp1 = cur_t1 - a * (1/m) * sum_1
# 同步更新两个参数
cur_t0 = temp0
cur_t1 = temp1
# 计算下下降后的误差
error = J(cur_t0,cur_t1)
print('error:%f, cur_t0:%f,cur_t1:%f'%(error,cur_t0,cur_t1))
# 下面是绘图
plt.scatter(datas.x, datas.y, label="Training data")
plt.plot(datas.x, datas.x*cur_t1+cur_t0, label="Prediction")
plt.legend(loc=2)
plt.show()
print(cur_t0,cur_t1)
gradient_descent()
样本数据在这里
还有就是,推荐自己动手写一遍这个代码,不是按我的写,是自己写,然后你会更了解其中的各个参数的功能,比如初始的\(\theta\)选取在不同位置、设置不同的学习速率a都会发生什么效果。
我去躺着了,拜拜~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号