条件概率、全概率公式、贝叶斯准则、独立性

害，选修课报了门人工智能，康康人工智能里需要的数学。。。只有概率论还没了解，但是概率又在人工智能领域里占很大比重，所以最近就又开始刷概率。

条件概率

条件概率和普通概率啥区别？

普通概率问题长这样：

你扔两次硬币，两次硬币都扔丢了的概率有多大

条件概率：

你扔两次硬币，第一次扔丢了，问两次都扔丢概率有多大

所以它就是已经确定了最后结果的部分信息，然后在这个基础上对剩下部分的概率进行推断。

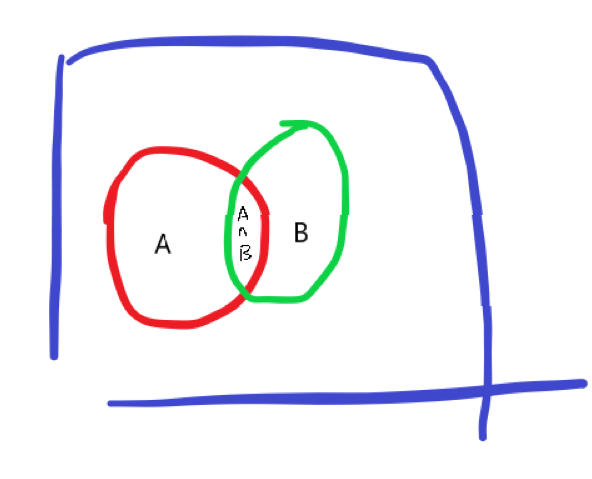
如果我们忽略上图尴尬的配色并假设\(A={第一次扔丢了},B={第二次扔丢了}\)，那么中间的\({A\cap B}\)就是所求的。

然后因为现在我们已经知道了第一次扔丢了，所以事件\(A\)已经发生了，结果肯定在\(A\)里，那么就需要更新\(A\)为整个样本空间替换原来的\(\Omega\)(即蓝色框框)。那现在所求的两次都扔丢的部分就得是\(\frac{P(A\cap B)}{P(A)}\)，这就是条件概率的公式。

\[P(B|A)=\frac{P(A\cap B)}{P(A)} \]

\(P(B|A)\)意思就是已知A发生了，B发生的概率，上面公式很自然，很容易想像。

我们可以把没有条件的概率想象成特殊的条件概率，它的条件就是结果肯定在整个样本空间\(\Omega\)中，所以\(P(B|\Omega)=\frac{P(\Omega \cap B)}{P(\Omega)}=P(B)\)

条件概率公式的变形

其实在大多数问题里，求的不是条件概率，而是已知条件概率，让你求\(P(A\cap B)\)，就比如如果天空中5%的概率出现飞机，出现飞机雷达有95%的概率检测出来，然后让你算雷达正确报警(有飞机并检测出来了)的概率。

所以可以把概率公式变下形状

\[P(A\cap B)=P(A)P(B|A) \]

同样的，也有

\[P(A\cap B)=P(B)P(A|B) \]

这两个公式在全概率公式和贝叶斯准则中都会用到

全概率公式

全概率定理是\(A_1,A_2,...,A_n\)是一组不相容的事件，并且形成样本空间的一个分割，而且对于每个\(i,P(A_i)>0\)，那么对于事件B

\[P(B)=P(A_1\cap B)+...+P(A_n\cap B)\\ =P(A_1)P(B|A_1)+...+P(A_n)P(B|A_n) \]

展现在图上就是这样，很自然，\(P(B)\)等于这些不相容事件与B的交集之和。

全概率公式用于解决类似这样的问题：

　你参加一个棋类比赛,其中50%是一类棋手,你赢他们的概率为0.3;25%是二类棋手,你赢他们的概率是0.4;剩下的是三类棋手,你赢他们的概率是0.5.从他们中间随机地选一位棋手与你比赛,你的胜算有多大?

贝叶斯准则

我们以往都是已知原因，推测结果。贝叶斯准则巧妙的利用了条件公式和全概率公式从结果反推原因的概率。

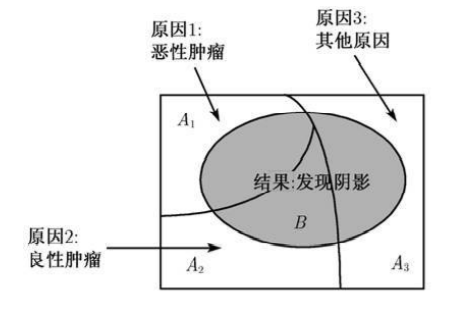
比如一个患者的检查结果是在胸部发现了阴影，设为事件\(B\)，造成阴影的原因可能有以上三个分别为\(A_1,A_2,A_3\)，现在要在已知发现阴影B的条件下每个成因A的概率\(P(A_i|B)\)

\[P(A_i|B)=\frac{P(A_i)P(B|A_i)}{P(B)}\\ =\frac{P(A_1)P(B|A_i)}{P(A_1)P(B|A_1)+...+P(A_n)P(B|A_n)} \]

上面就是贝叶斯公式，关于分母，用了条件概率的变形，分子则是用了全概率公式。

独立性

如果事件A发生对事件B的概率没有影响就称为两个事件是独立的。

就比如你抛两次硬币，已知你第一次抛的是正的，问第二次抛的是正的的概率，它依然还是1/2。

所以两个独立事件满足

\[P(A|B)=P(A)\\ P(B|A)=P(B) \]

不过上面的两个公式有限制，因为条件概率中限制条件发生的概率不能为0，变形可得

\[P(A\cap B)=P(A)P(B) \]

这样对A和B就都没有不为0的限制了。

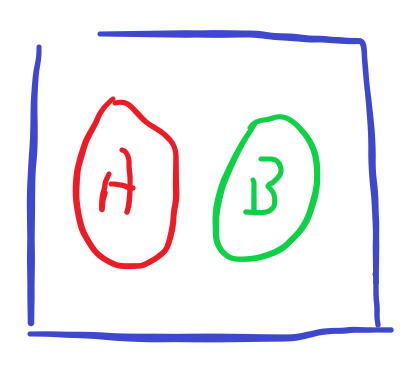
很容易把两个事件的独立关系理解成上面的图，但是上面图中的AB并不独立，因为它们其中一个发生，另一个就肯定不会发生，也就是一个事件是否发生受另一个的影响。

如果非要用图表示，独立性可以这样画

假设图中每个蓝色块的概率是1/4，红色事件(1/2)和绿色事件(1/2)就是互相独立的，它们有交集(1/4)且交集正好等于彼此的一半

用上面的公式证明

\[P(红\cap 绿)=P(红)P(绿)=1/2\times 1/2=1/4 \]

条件独立

在给定条件C下，若AB满足

\[P(A\cap B|C)=P(A|C)P(B|C) \]

则AB在条件C下独立，可以导出另一个特征

\[P(A\cap B|C)=\frac{P(A\cap B\cap C)}{P{C}}\\ = \frac{P(C)P(B|C)P(A|B\cap C)}{P(C)}\\ =P(B|C)P(A|B\cap C) \]

若\(P(B|C)\not = 0\)，把这个式子和上面的联立就得到

\[P(A|B\cap C)=P(A|C) \]

但是AB相互独立并不说明它们在条件C下独立

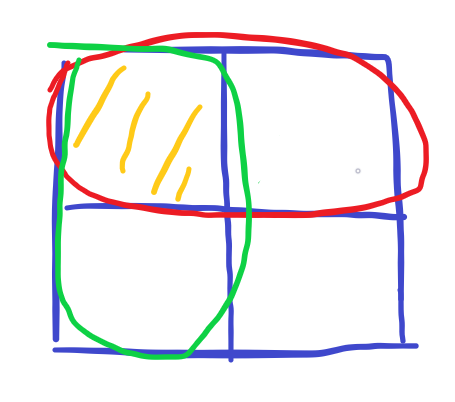
这个图可能有些乱了...没啥大事，A是红的，B是绿的，C是黄的，我们知道AB是相互独立的，但是\(P(A|C)\)和\(P(B|C)\)并不相互独立

\[P(A|C)=P(B|C)=1/2\\ P(A\cap B|C)=0\\ p(A\cap B|C)\not =P(A|C)P(B|C) \]

一组事件独立

\[P(A_1\cap A_2\cap A_3)=P(A_1)P(A_2)P(A_3) \]

一组事件两两独立无法推测出这组事件相互独立

还是上面那个神图

ABC两两独立，但是它们的交集不等于它们各自概率的乘积，他们的交集是0，概率乘积是1/8