行列式

矩阵A的行列式记作$detA$，他是一个数

性质 1#

单位矩阵的行列式为1

性质 2#

行交换会反转行列式符号

$$\begin{vmatrix} 1&0\\ 0&1 \end{vmatrix} = 1 \,-> \,\begin{vmatrix} 0&1\\ 1&0 \end{vmatrix} = -1$$

目前为止已经能用这两个性质导出二阶(2x2矩阵)行列式的公式了

二阶行列式公式#

$detA = ad-bc$

置换矩阵行列式#

置换矩阵就是行交换过的单位矩阵，所以根据性质1,2，置换矩阵行列式只可能是1或-1

性质 3#

性质 3.1#

对于每一行上的公因数，都可以提到外面

$$\begin{vmatrix} ta&tb\\ c&d \end{vmatrix} = t \begin{vmatrix} a&b\\ c&d \end{vmatrix}$$

$$\begin{vmatrix} ta&tb\\ tc&td \end{vmatrix} = t^2 \begin{vmatrix} a&b\\ c&d \end{vmatrix}$$

性质 3.2#

对于每一行，可以拆解，具有线性性

$$\begin{vmatrix} a+a'&b+b'\\ c&d \end{vmatrix} = \begin{vmatrix} a&b\\ c&d \end{vmatrix}+ \begin{vmatrix} a'&b'\\ c&d \end{vmatrix}$$

注意，这不是说$det(A+B)=detA+detB$，以上法则只单独对每一行成立

性质 4#

如果两行相等，行列式为0

我们可以用性质2证明

$$假设detA=l，A中有两行相等\\ 交换这两行，detA'=-l，由于A'=A，所以detA'=l\\ l=-l，l为0$$

性质 5#

行列式不因消元而改变

可以从性质3和4证明

$$\begin{vmatrix} a&b\\ c&d \end{vmatrix} = \begin{vmatrix} a&b\\ c-ta&d-tb \end{vmatrix}= \begin{vmatrix} a&b\\ c&d \end{vmatrix}-t \begin{vmatrix} a&b\\ a&b \end{vmatrix}= \begin{vmatrix} a&b\\ c&d \end{vmatrix} - 0$$

性质 6#

矩阵中如有一行是0，行列式为0

性质 3.1可以证明它

假设有一行是0，则有

$$\begin{vmatrix} a&b\\ 0&0 \end{vmatrix} = 0\times \begin{vmatrix} a&b\\ 0&0 \end{vmatrix} = 0$$

所以可以推出之前的结论：

不可逆矩阵的行列式为0（因为不可逆矩阵必会消元出现零行）

至此为止，我们学的6条性质大概也就只能计算二阶行列式，好难受吼...sadly

性质 7#

三角矩阵的行列式为对角线之积(不看符号的话)

可以从性质5和3证明

对于三角矩阵对角线下方一定是全0的（或者上方全0），然后我们可以继续向上消元，直到就剩主元，也就是对角线

$$\begin{vmatrix} d_1&0&...&0\\ 0&d_2&...&0\\ ...&...&...&...\\ 0&0&...&d_n \end{vmatrix} = 0\times \begin{vmatrix} a&b\\ 0&0 \end{vmatrix} = d_1\times d_2\times ... \times d_n \begin{vmatrix} I \end{vmatrix}$$

因为消元会用到行交换，所以符号要根据行交换次数判断。

这下就能算所有矩阵的行列式了，只需要一次消元即可，也就是说行列式等于主元之积(如有行交换需要根据性质2来乘一个1或-1)

性质 8#

$detA=0$当且仅当$A$是奇异矩阵

也就是当且仅当矩阵不可逆，这个没啥可证明的...

性质 9#

$detAB=detA\times detB$

证明：把两个矩阵化成对角矩阵，事实上只要非奇异矩阵一定能化，因为这相当于解方程组嘛，然后利用性质7一下就看出来了呢~~我不太想写过程了

根据这个我们可以推出

• $detA^{-1}A=1$
• $detA^2=(detA)^2$

性质 10#

$det A^T=detA$

根据性质7能推出，因为矩阵转置后对角线不变

这个性质厉害了，上面我们所有矩阵行列式性质都是从行的角度出发的，有了性质10，就相当于行列式所有对于行的性质对列同样适用

给出老爷子的证明~

$$Prove: |A^T|=|A|\\ |U^TL^T|=|LU|\\ |U^T||L^T|=|L||U|\\ |U^T|=|U|\\ check√$$

思想就是用LU分解，因为L是一个下三角阵，对角线都是1，所以行列式为1

行列式通用求解公式#

根据上面的性质可以这样计算$2\times 2$矩阵行列式

$$\begin{vmatrix} a&b\\ c&d \end{vmatrix}= \begin{vmatrix} a&0\\ 0&d \end{vmatrix} \begin{vmatrix} 0&b\\ c&0 \end{vmatrix}=ad+(-cb)$$

也就是分解成每行每列只剩一个元素的矩阵，再通过行交换变成对角矩阵（并确定行交换产生的正负号），主元相乘，再把所有结果相加就好了。对于$n\times n$矩阵。就有：

$$\sum_{i=1}^{n!}\plusmn a_{1\alpha}a_{2\beta}a_{3\gamma}...a_{n\omega}$$

也就是对于$n\times n$矩阵需要累加$n!$次

$\alpha \beta \gamma$等这些下标是不确定的，关键看当前行选择的列，但只要这三个不相等就行了，它是$1,2,3,...,n$这些数的一个排列。比如上面例子的$2\times 2$矩阵就是$a_{11}a_{22}+(-a_{12}a_{21})$

代数余子式解法#

对于大矩阵，上面的算法简直是灾难。。

代数余子式把$n\times n$的形式简化为$n$个$n-1$形式，如果你想，可以一直化下去

原理就是对于上面的大公式，可以提取公因式

$$a_{11}(...+...)+\\ a_{12}(...+...)+\\ a_{13}(...+...)...$$

画图就是这样的

就是说我们如果选择了$a_{11}$这行这列的其他元素都不能选了，这时我们只需要计算选择$a_{11}$后剩余的那个$2\times 2$矩阵，而这个矩阵的行列式就是上面括号里的内容，也就称为$a_{11}$的代数余子式。

对于一个大矩阵，分别选择第一行的每一个元素，然后乘以它的代数余子式，相加就是行列式，如果使用了代数余子式，问题规模仍然很大，可以对代数余子式再次使用代数余子式，这下就把问题规模不断缩小。哈哈哈这就是分治策略吧~~

嘶。。。行列式里我们永远要注意的就是正负号，在代数余子式求行列式法里正负号看当前选择元素行标列标之和，奇数就是负，偶数就是正。

主元解法#

奶奶腿的，上面两个都太难了，我这种十以内加减法还偶尔算错的死小孩真的驾驭不了

我感觉还是主元解法简单...很多矩阵因为存在线性相关行列，所以可以一眼就看出行列式。

ohhh上面已经介绍过了，就不写了。

行列式几何意义#

行列式可以给出很简洁的求逆和解方程的公式，但是它虽然漂亮却没之前的方法好用。所以不记了~~

来看行列式的几何意义

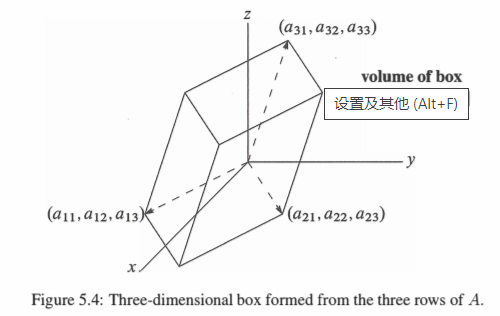
在$3\times 3$矩阵中，行列式的几何意义就是矩阵的体积的绝对值。

就是上面这样，它代表以矩阵的每行为一条边所组成的立方体的体积。

思考单位矩阵的行列式，不正是由三条边撑开的一个单位立方体的体积吗，所以是1。

对于长方体，我们可以看作立方体的某个边扩大了c倍，也就是矩阵的某行扩大c倍，几何上体积也扩大c倍，行列式也扩大c倍（因为可以提取公因数，性质3.1）

对于平行四边体，可以看作矩阵某行加了一些数，比如二维情况下可以看作：

$$\begin{vmatrix} a+a'&b+b'\\ c&d \end{vmatrix}$$

知道了行列式的几何意义，那么为啥不可逆的矩阵行列式为0也出来了，因为存在线性相关列，所以它顶多撑开一个平面，平面可哪有体积啊

2020/04/16 UPDATE 逆序数与行列式#

学校的线代开课了，从逆序数的角度看行列式，看到了些不同的东西，这些不同的东西和之前以消元角度看行列式得到的结论惊人相似，哈哈哈数学确实挺美就是和妹子差点。

上面给出了这样一个n阶行列式通用大公式

$$\sum_{i=1}^{n!}\plusmn a_{1\alpha}a_{2\beta}a_{3\gamma}...a_{n\omega}$$

但是，上面的公式还是有瑕疵，前面的正负不明确，需要数经历了几次行互换，但通过逆序数的概念就可以明确这个正负号了，如果把行列式每项的行标按正常顺序排列，那么对应列标的逆序数为偶数这项就是正号，反之就是负号。关于逆序数就不写太多了，可以去百度下。

其实可以把这个逆序数看作列交换次数，也可以看作转置的行交换次数，我们知道转置不改变行列式的值，而行交换会改变，所以上面的逆序数决定正负号就理所应当了。

参考资料#

• MIT线性代数公开课 - bilibili