投影、最小二乘法介绍
二维空间
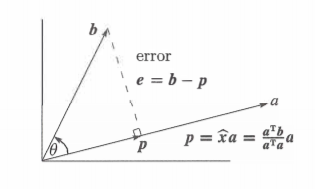
假设a是二维空间一个子空间，现在我们要求解\(ax=b\)，但是就像下面这张图，\(b\)并不在\(a\)的列空间里，所以也就没解
但是没办法吼，领导就是要一个解，那咋办？我们只能找一个最接近的解，我们在二年级的时候学过，\(b\)到\(a\)上肯定是垂线段最短，所以我们就画个垂线。这下得到了一个误差向量\(e\)和一个向量\(p\)，我们叫它投影。我们要做的就是用\(A\hat{x}=p\)代替原\(Ax=b\)，\(\hat{x}\)则是我们要找的原方程的最优解。它们有如下关系：
- \(p\)在\(a\)列空间中（p就在a上）
- \(e\)和\(a\)垂直
对应上面的12，我们可以推导出如下公式
- \(p=\hat{x}a\)
- \(a^T(b-\hat{x}a)=a^T(b-p)=0\)
把它们整理成关于x，关于p的完整式子
-
\(\hat{x}={a^Tb \over a^Ta}\)
-
\(p=a{a^Tb \over a^Ta}\)
上面的式子的后半部分就是把\(b\)投影到\(a\)上得到投影\(p\)的矩阵，称为投影矩阵\(P\)
- \(P={aa^T\over a^Ta},p=Pb\)
二维投影矩阵的性质
- \(P^{-1}=P\)，对称，因为一个矩阵乘自己的转置总是对称的
- \(P^2=P\)，做两次投影仍会落在原位，这从几何上很好理解
高维空间投影
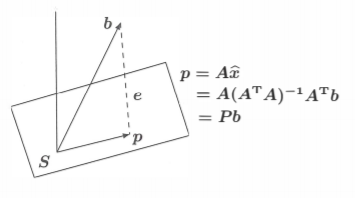
二维空间的那些东西很容易推广到高维，用三维举例。
这和二维空间没啥差别，只是个别公式需要稍微调整下，同样可以导出这些性质
- \(p\)在\(A\)列空间中
- \(e\)和\(A\)列空间垂直
- 所以可以知道\(e\)在\(A^T\)的零空间中，也就是\(e\)在\(A\)的左零空间
公式
- \(p=A\hat{x}\)
- \(A^T(b-A\hat{x})=A^T(b-p)=0\)
整理
- \(A^TA\hat{x}=A^Tb\)
- \(\hat{x}=(A^TA)^{-1}A^Tb\)
- \(p=A\hat{x}=A(A^TA)^{-1}A^Tb\)
- \(P=A(A^TA)^{-1}A^T\)
这些都是根据二维空间的例子改的，不懂可以联系之前的二维空间想象。
为啥之前二维空间可以直接把\(a^Ta\)除过去而不用求逆呢？对那个例子，这个乘法是一行乘一列，所以得出来一个数，也就没啥影响。
看上面的第四个公式，如果A是\(n\times n\)可逆方阵，那么正好P等于单位阵，因为如果A是可逆方阵说明A的线性组合铺满整个n维空间，所以必有解。也就是说b就在A列的线性组合中，也就不用投影。
N维投影矩阵性质
- 对称，\(P^T=P\)\[(A(A^TA)^{-1}A^T)^T=A(A^TA)^{-1}A^T \]
- \(P^2=P\)\[P^2=A(A^TA)^{-1}A^TA(A^TA)^{-1}A=A(A^TA)^{-1}A^T=P \]
最小二乘法
上图有三个点，我们并找不出一条直线穿过三个点，所以对于\(Ax=b\)(b由这三个点组成)并找不出一个合适的\(x\)。这时就希望拟合出一条误差最小的直线
这就是我们上面说那么多的目的
假设最优直线是\(b=C+Dt\)，那么可列出三个方程
写成\(Ax=b\)就是
我们知道是不可能找出\(C,D\)的，但是根据上面的经验，我们可以对两边乘一个转置，得到一个有解的方程：\(A^TA\hat{x}=A^Tb\)，把\(A^TA\)看作一个整体，\(A^Tb\)看作一个整体按照以往步骤消元
得出两个方程组，就能得出cd了，也就找到了最优解那条直线（这书上给的例子数不好算啊，，不写出来了）
