Loading

单源最短路径(Bellman-Ford算法)

单源最短路径和广度优先搜索要做的事很像。

关于广度优先搜索可以看图算法这一篇笔记。

单源最短路径给定一个源s，当算法执行完毕，找出从源s到图中的每个顶点权重最小的一条路径。

其实广度优先搜索可以看作特殊情况的单源最短路径，在广度优先搜索解决的图中，所有的边权重都为1。

注意： 本篇笔记说的最短路径都是指权重最低的路径，并非通过的边数最少的路径

负权重

某些单源最短路径问题的算法中允许出现负权重的边，就比如我们要讨论的Bellman-Ford算法。

但是有些算法不允许，比如Dijkstra算法。

关于环路

单源最短路径问题中能不能存在环路呢？我们分情况讨论。

  1. 权值为正的环路
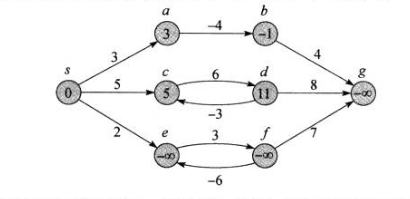
    我们看s到c的路径，这个路径包含一个环路，即节点c和节点d。我们从s出发，到c之后还可以走无数次c和d构成的环路，最终都能回到c。但是由于我们每从c走到d，权重就会加6,再从d走回c会减3，所以每次绕环是需要额外花费3的权重的。所以我们最终的找出的最短路径中不可能存在权值为正的环路。
  2. 权值为负的环路
    看s到e的路径，和上面的分析一样，每次绕e和f组成的环，会减去3的权值，所以这种情况已经不存在最短（权重最低）路径了，因为每次绕环权值都会更小，所以最短的路径应该是负无穷。这种情况算法得不到正确的答案。我们的Bellman-Ford算法会检测到负值环，并返回False通知调用者。
  3. 权值为零的环路
    这种情况无论绕环走多少次都无影响，所以我们可以重复删除这些环路，最后得到一条不包括环路的最短路径。

综上所述，算法最后找到的最短路径中应该不包含环路，即都是简单路径。

松弛操作

我们来看下单源最短路径算法的核心操作。松弛。

对于每个节点v，维持一个属性v.d，这个属性用来维持源s到v的最短路径估值。它是s到v的一条最短路径权重的上界。

对于每个节点v，维持一个属性v.PI，这个属性和d配合，用于记录当前的估值情况下和v连接的前驱节点。

提供一个权重函数w(u,v)计算u和v构成的边的权重

我们给每个节点的d和PI初始值定为无穷和NIL。把源节点s的d定为0

INITIALIZE-SINGLE-SOURCE(G,s)
    for 图G中的每个节点 v
        v.d = ∞
        v.PI = NIL
    s.d = 0

提供松弛函数RELAX(u,v,w)对边(u,v)进行松弛，参数w是权重函数。

松弛函数其实就是测一下如果经过u的话会不会对节点v的最短路径估值d起到优化。在说通俗点就是测试连接(u,v)的话会不会让当前s到v的最短路径估值更小。如果是就连接(u,v)

RELAX(u,v,w)
    if v.d > u.d + w(u,v)
        v.d = u.d + w(u,v)
        v.PI = u

对溜，就是这样，如果当前节点v的估值大于u的估值加边(u,v)的权重的话就重置v的估值为u.d+w(u,v)并设置v的前驱节点为u。

最短路径和松弛操作性质

我们假设sp(s,v)是从源s到节点v的最短路径的权重

  1. 三角不等式性质： 对于任何边(u,v)我们有sp(s,v) <= sp(s,u) + w(u,v)
    啥意思呢，就是说明对于每个边，要么就是最短路径里需要走这条边，这时不等式中的小于号拿掉，变成等式。要么就是可以有一条不经过`(u,v)的更短的路径通往v。
  2. 上界性质：对于所有节点v，总有v.d >= sp(s,v)。
    这是一条关于松弛操作的性质，我们不断调用松弛操作去调节节点v的最短路径估值d，一旦发现更短的路径就更新它，直到v.d == sp(s,v)后，松弛操作将永远找不到更短的路径，v.d就永远不会更新了。
  3. 非路径性质：如果s到v之间不存在路径，则v.d == sp(s,v) == ∞。
    很正常，如果不存在路径，那么v的估值永远得不到更新，一直是无穷。
  4. 收敛性质：对于某些节点u,v，如果s⇝u→v是图中的一条最短路径，并且在对边(u,v)进行松弛前的任意时间有u.d == sp(s,u)，则在之后的所有时间有v.d == sp(s,v)。
  5. 路径松弛性质：如果p=(v0,v1,...,vk)是从源节点s=v0到节点vk的一条最短路径，并且对p中边的松弛次序为(v0,v1),(v1,v2)...(vk-1,vk)，则vk.d == sp(s,vk)。该性质的成立与其他任何松弛操作无关，即使这些松弛操作是和对p上的边所进行的松弛操作穿插进行的。
    因为p是最短路径，所以每次按上面顺序进行松弛估值一定会更新到最短的路径啊。毋庸置疑。这条和第四条差不多啊。
  6. 前驱子图性质：如对于所有节点v，一旦v.d == sp(s,v)则前驱子图是一颗以跟节点为s的最短路径树。
    这性质在“关于环路”那个段落里其实已经隐含了，因为最短路径一定是不包含环路的简单路径，所以肯定是一棵树。

不好意思题外话。。。🐎了个🥚，抄书好累啊，但是我不得不把算法导论翻译成人话，没错我在逼自己看懂它。。。

有了上面的分析，我们可以开始研究主角Bellman-Ford算法了

Bellman-Ford算法

Bellman-Ford算法可以工作在不存在从源节点可以达到的权重为负值的环路的图。

如果存在这样的图，算法将返回False通知用户无法给出正确可靠的结果。

算法通过不断对每条边进行松弛来一点点的使每个节点v的最短路径估值d一点一点的下降，最终达到sp(s,v)。

其实对于每一次对所有边挨个进行松弛操作，必定会有至少一条边的d值会被设置为正确的。这样只需要对图的每条边进行图中节点数减1次循环就可以计算出每个节点正确的最短路径估值。所以我们这样编写BELLMAN-FORD算法：

BELLMAN-FORD(G,w,s)
    INITIALIZE-SINGLE-SOURCE(G,s)
    for i = 1 to |G.V| - 1
        for G中每个边 (u,v)
            RELAX(u,v,w)
    for G中每个边 (u,v)
        if v.d > u.d + w(u,v)
            return FALSE
    return TRUE

But，，why???下面证明下。

算法能得到正确估值的证明

假设图不包含从源节点s可以到达的权重为负值的环路，我们考虑每一个可以从源到达的节点v肯定有一条最短路径p={v1,v2,...,vk}。s=v1，v=vk。由于我们前面的前驱子图性质，所以这个最短路径肯定是一个简单路径，即没有环。那么这条路径里就最多有图中节点数量-1个边。再根据前面的路径松弛性质，只要这条最短路径是按顺序松弛的，那么就可以得到正确的d值，和其它松弛操作的顺序无关，那么每次外层for循环都松弛所有的边，那么在第i次松弛操作时被松弛的边肯定包含(vi-1,vi)，所以，v.d==vk.d==sp(s,vk)==sp(s,v)d就是对的喽。

迄今为止，我们还有一个坑没有解决。那就是算法的返回值。

算法是否会在存在负权环路时返回FALSE，在正常情况下返回TRUE呢？

算法能得到正确返回值的证明

先看看算法导论的证明，确实很严谨很正确。不过我下次复习看这个笔记的时候。。。我这笨脑袋肯定还得想半天。

所以得想想怎么说才能让我下次一下就能懂。

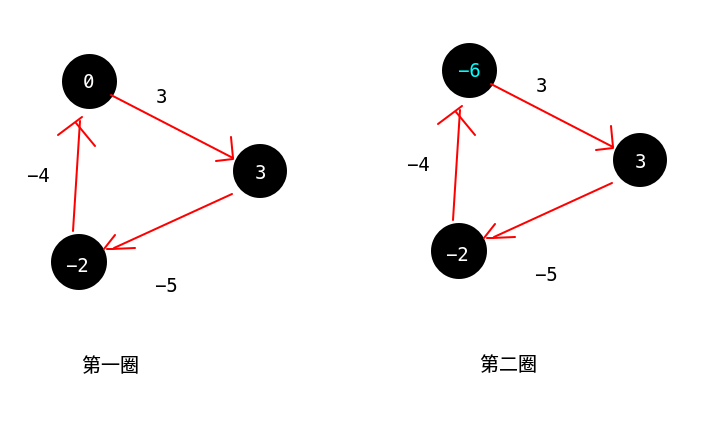
emmm。。。看这。。。。图？？？假设有这么一个负权环，从上面的节点开始，假设初始状态那个顶上的节点的d是0，在第一圈到左下脚的节点时，还是满足v.d<=u.d+w(u,v)的。不会返回FALSE，不过当它转了一圈后再来就有问题了。会产生v.d>u.d+w(u,v)。而且随着圈越转越多这个差值会越来越离谱。

每次遍历所有边就必定要走一遍环路。所以到最后只需检查v.d>u.d+w(u,v)即可。算法是正确的

参考资料

posted @ 2020-02-18 13:21  yudoge  阅读(1038)  评论(0)  编辑  收藏  举报