最小生成树
最小生成树是一个图问题。
我们有一个带权重的无向图，找到一个权重最低的路径连通无向图中的所有节点，这条路径如果展开看的话就是一棵树，这棵树就是最小生成树。
权重为边的一个属性，在最小生成树问题里，你可以理解为如果要通过这条边所需要的花销，当然权重具体表达的含义还得看具体问题。比如在寻找最短路径问题中，权重可以理解为两个节点之间的距离。
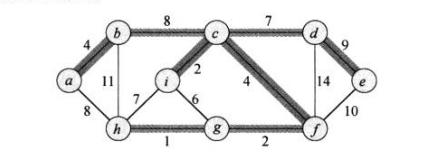
图示就是一个最小生成树的例子，阴影就是最小生成树的边。最小生成树不唯一，例如上图删除(b,c)，加入边(a,h)也是一颗最小生成树。
嘶，看到这就莫名想到贪心算法哈，没错，即将讨论的两个常见的最小生成树的算法都是贪心逻辑。贪心算法可以看我的另一篇博文：贪心算法
通用算法
我们有这样一个最小生成树的通用算法：
GENERIC-MST(G,w)
A = ∅
while A不是一个生成树
找一个边(u,v) 此边是A的安全边
A = A ∪ {(u,v)}
return A
算法第一行初始化A为一个空集，然后进入循环，如果A不是一个生成树，就一直循环，循环体里找一个边(u,v)是A的安全边，把它加入集合A，直到A是一个生成树，就返回。
这是一个贪心策略，每次找一个当前情况下A的安全边，这条安全边肯定存在，当A中的边已经能够连通图G中所有节点了，A肯定会构成一个最小生成树。
我们来解释一下安全边的定义然后在说明以下此贪心算法的正确性。
安全边
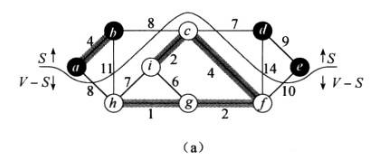
我们将无向图G切割，如下图
首先，看下算法导论的解释。如果此次切割没有切到集合A中的边，称切割尊重集合A。在这次切割切到的所有边中，权重最小的边就是轻量级边。它不一定是惟一的，比如上图中的(a,h)和(b,c)。像这样一条轻量级边就是对A安全的，称为安全边。这里要注意一定要满足几条性质。
- 切割尊重集合A
- 切割到的边中最小的一条边是轻量级边
其实什么安全边，又切割的，就是选一个不在A中的并且能和A中已有边构成树（而不是环）的权重最小的边
什么？这个算法为啥正确？选一个权重最小的总比选大的好嘛。。。所有权重最小的边构成的生成树难道不是最好的？
你看哈，假如你想去A市的10家超市，有20条路设在这些超市之间，它们之间能组合出一条或多条连通的路你可以选择，那你当然是尽量不绕弯（不走重复路），尽量走短的，尽量一次走完了。那切割的过程就是尽量不绕弯，并且尽量一次走完，然后选边的过程就是走短的嘛。
算法的奥妙在于如何选这条安全边，毕竟计算机可不像你能划线分割，就算硬写出一个算法实现了划线，那在数据量巨大的图里工作也是不太合适的。
Kruskal算法
Kruskal算法把图中的所有顶点看成一片森林，最开始每个顶点是一颗单独的树，就是说森林里所有顶点都是单个的，不相连。
把图中所有边从小到大排序，依次选择，选择的条件是边连接的两个节点属于不同的树。每次选择到一条这样的边，这条边就是最小生成树的一条边，把这两棵树合并即可。
概算法依赖不相交集合数据结构，API如下：
// 具体见算法导论 高技数据结构篇 21.1
MAKE-SET(u) 创建一个只包含元素u的集合
FIND-SET(u) 返回包含元素u的集合代表元素
UNION(u,v) 合并两个集合
MST-KRUSKAL(G,w)
A = ∅
for 图G里的每一个顶点v
MAKE-SET(v)
edgeSet = 根据边的权重w按从小到大排序图里的每条边
for edge in edgeSet
// 判断u v是否在一棵树中
if FIND-SET(u) != FIND-SET(v)
A = A ∪ {(u,v)}
UNION(u,v)
return A
该算法时间复杂度依赖不相交集合数据结构，不展开分析。
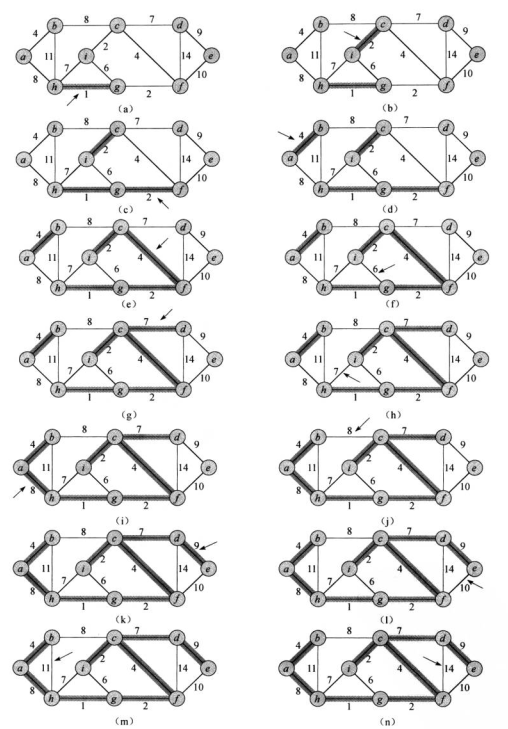
如下是Kruskal算法在一个图上的执行过程
Prim算法
Prim从r开始，每步选择一个连接集合A和集合A之外的节点的最小边，最终推进到树连通整个图
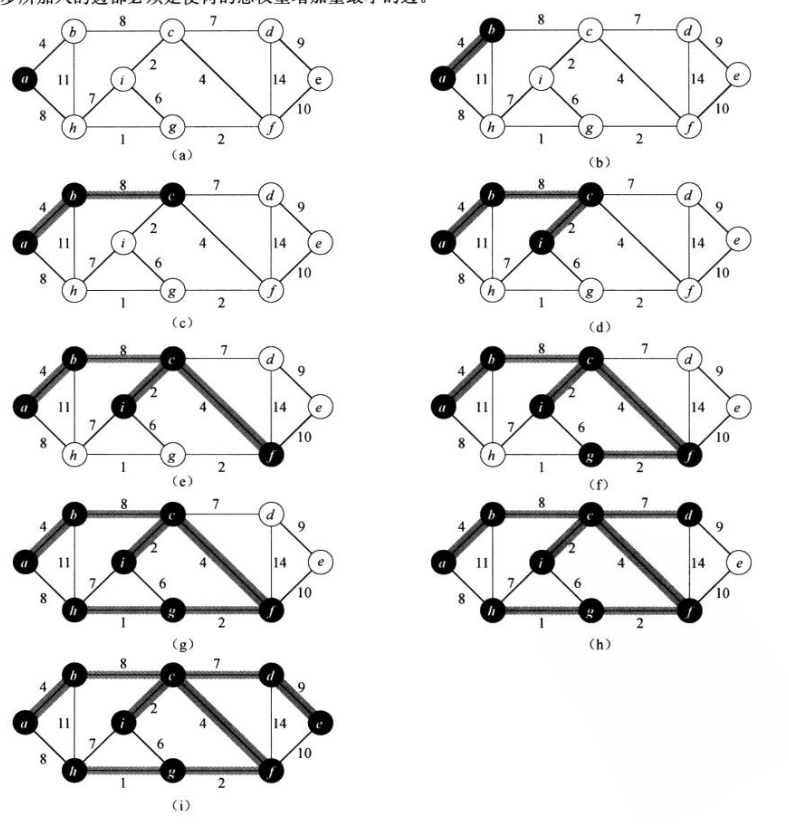
如下是Prim算法的工作过程
看得出和Kruskal算法的差别，Kruskal算法并不限制选择的边必须连接A和集合A之外。
Prim算法借助一个基于key属性的最小优先队列里（EXTRACT-MIN方法总是弹出key属性最小的元素），对于节点v，v.key保存连接v和树中节点的所有边中最小边的权重。如果不存在这样的边，则v.key=∞。v.PI则是v在树中的父节点。
MST-PRIM(G,w,r)
for 图G中的每个节点u
u.key = ∞
u.PI = NIL
r.key = 0
Q = G中节点集合
while Q != ∅
u = EXTRACT-MIN(Q)
for v in G.Adj[u]
if v in Q and w(u,v)<v.key
v.PI = u
v.key = w(u,v)
