图算法

之前写过一篇图的笔记，但是当时了解的还是不够深入，当时读那本算法都是递归实现的，我看的也有点懵逼。最近再看算法导论，正好看到图了，再记一遍。

本篇笔记使用Python代码实现

图可以分为有向图和无向图，区别从名字可以看出。

我们先看看图的实现方式，图有两种常见的实现方式，邻接链表和邻接矩阵。

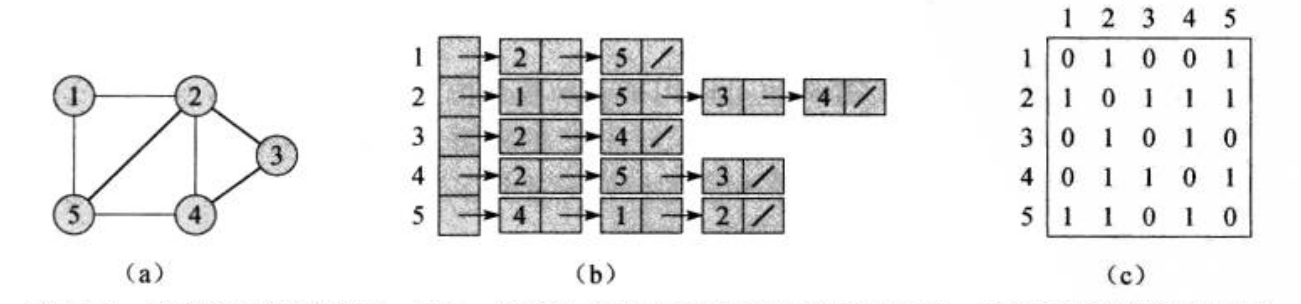
上图中是用邻接链表(b)和邻接矩阵(c)表示一个无向图(a)

邻接链表把图中每个节点的与之连通的节点记录成一个链表，假设有邻接链表L，若L[u]所连接的链表中存在v，则说(u,v)连通。

邻接矩阵则是使用一个二维数组，记录每两个节点的连通状态，假设我们有邻接矩阵M，若M[u][v] == 1则说(u,v)连通，否则不连通。

通过上图可以发现：

1. 对于稀疏图，邻接链表的数据结构有更好的紧凑性，而邻接矩阵需要记录大量没用的0值来表示两个节点不连通，所以邻接矩阵的空间复杂度更高
2. 邻接链表查询节点是否连通需要遍历链表，是线性时间复杂度，而邻接矩阵只需要O(1)时间复杂度，即判断M[u][v]==1
3. 对于无向图来说，邻接矩阵表示的无向图是一个对称矩阵，也就是说M=M^-1，这使得邻接矩阵可以只记录一半的元素，节省空间，而邻接链表则不行

总的来说，各有利弊，在笔记中统一使用邻接链表来表示矩阵，并提供如下的API。

class Graph
    # initialVertex  -- 初始化节点列表 默认为空
    constructure(initialVertex=[]) -- 构造方法
    Adj(i) -- 表示图中所有和i连接的元素
    vertices() -- 返回图中所有节点
    @staticmethod
    SampleGraph() -- 返回一张测试图 供算法调用

    # 以下方法在笔记中没有调用 可以忽略
    addVertex(v) -- 向图中加入节点
    addVertices(vs) -- 向图中批量加入节点
    union(u,v) -- 测试u v是否连通
    connect(u,v)  -- 连通u v
    

Graph的所有代码

# 我们在自己的算法中会保证以下API被正确的调用
# 所以，为了简洁起见，下面的图实现中没有任何保护性代码
# 并且也没考虑任何时空复杂度的问题
# 如果自己实现图并用作业务逻辑的话，可别这么写
class Graph:
    def __init__(self,initialVertex = []):
        self._graphTable = {}
        self.addVertices(initialVertex)

    def addVertex(self,v: int):
        self._graphTable[v] = []

    def addVertices(self,vs):
        for v in vs:
            self.addVertex(v)
    
    def union(self,u,v):
        for i in self._graphTable[u]:
            if i == v:
                return True
        return False

    def connect(self,u,v):
        self._graphTable[u].append(v)
    
    def Adj(self,u):
        return self._graphTable[u]

    def vertices(self):
        return self._graphTable.keys()

    @staticmethod
    def SampleGraph():
        g = Graph([0,1,2,3,4,5,6,7,8,9])
        g.connect(0,1)
        g.connect(0,5)
        g.connect(0,9)
        g.connect(8,3)
        g.connect(1,4)
        g.connect(4,7)
        g.connect(7,6)
        g.connect(6,0)
        g.connect(2,4)
        g.connect(6,2)
        g.connect(3,9)
        g.connect(9,7)
        return g

本篇笔记主要记录图的两种搜索算法，深度优先搜索和广度优先搜索，为了和算法导论的API保持一致，又提供了如下的搜索辅助类Search。

WHITE = 0
GRAY = 1
BLACK = 2

INF = float("inf")
class Search:
    def __init__(self,G):
        self.G = G
        # d用于辅助搜索算法工作
        self.d = {}
        # pi用来记录每个节点的直接前驱节点
        self.PI = {}
        # color用来记录每个节点的颜色，搜索算法需要使用颜色辅助
        self.color = {}
        # 用来辅助搜索算法工作
        self.f = {}

        # 初始化默认值
        # init d
        for i in G.vertices():
            self.d[i] = INF

        # init PI
        for i in G.vertices():
            self.PI[i] = None
        
        # init color
        for i in G.vertices():
            self.color[i] = WHITE

        # init f
        for i in G.vertices():
            self.f[i] = INF

之所以把这写东西单独做成一个类，是因为这些属性只在搜索算法中会用到，所以没有放在图数据结构中。之所以没放在具体的搜索算法里，是因为不想让这些属性和具体的搜索算法耦合，而是让所有的即将讨论的搜索算法都可以使用。

好了，一切都准备好了，开始搜索算法的学习

广度优先搜索

先学的是广度优先搜索(BFS)，从名字就可以联想到警察抓捕犯人时地毯式搜索的情景。BFS检查当前节点的每个直接后继节点，当全部的直接后继节点检查完毕，再检查每个直接后继节点的子节点

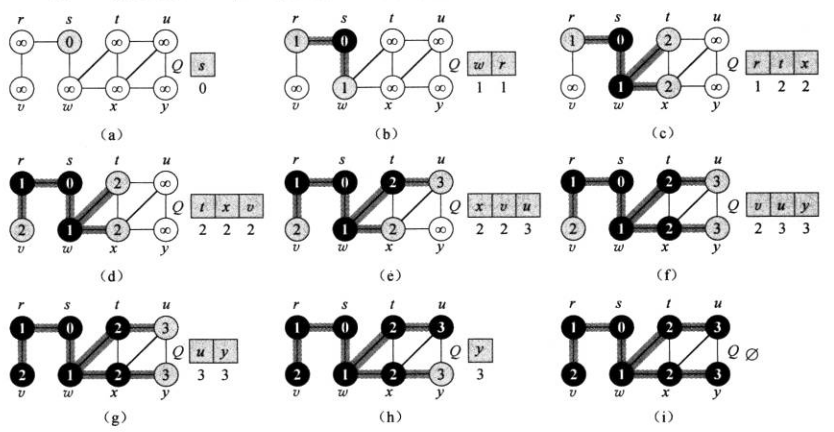
图为BFS在一个图中以s为源节点的推进过程。

BFS中，把未探索的节点标记为白色，把已探索并且所有直接后继都已经被探索的节点标记为黑色，把已探索但并非所有直接后继都已经被探索的节点标记为灰色。算法先把s标记为灰色，在探索s的所有直接后继节点，然后把它们标记成灰色，这时，s的所有直接后继节点被探索，所以把s标记为黑色，然后再去探索上一个过程中发现的黑色节点。以此类推，直到遍历整张图。

我们在每个节点上记录一个属性d，它表示与源节点的距离，源节点的d属性被设置为0。如果不能到达源节点，则d为无穷。每次发现一个节点，我们更新它的d为它的直接前驱节点的d+1

广度优先搜索依赖一个队列实现，我们现在写下它的代码：

from graph import Graph
from search import Search,WHITE,BLACK,GRAY
def bfs(G,C,s):                                                                 
    # 设置源的颜色为灰
    C.color[s] = GRAY
    # 初始化队列
    queue = [s] 
    while len(queue) != 0:
        u = queue.pop(0)
        for v in G.Adj(u):
            if C.color[v] == WHITE:
                C.color[v] = GRAY
                C.d[v] = C.d[u] + 1 
                # 记录v的前驱节点
                C.PI[v] = u 
                # 入队列等待被探索
                queue.append(v)
        C.color[u] = BLACK

g = Graph.SampleGraph()
s = Search(g)
bfs(g,s,0)

如上就是广度优先搜索的代码，关于原理上面已经说的差不多了，相信结合代码基本看懂没啥问题。

最短路径

执行广度优先算法遍历到节点u时，算法所走的路径就是源到它的最短路径。并且由于节点每深入一层，d属性就加一，所以u.d就是源到d的最短路径经过的节点数。下面我们说说为啥算法能走出最短路径，关于数学论证，算法导论里很详细，但是那对不喜欢数学的人显然是一场噩梦，所以我尽量说的通俗。

广度优先算法每次深入一层，这点从上面的图片和代码中都能看出，意思就是，假设我们从s出发，那么先探索的是s的下一层的节点，然后再探索每个下一层节点的下一层，所以队列里的节点的深度或者说路过的节点数都是一样的（有时会有上一层节点，那么深度差1），所以如果每次只深入一层，那么如果s和u能连通，并且有多条路径连通，肯定是最短的那条先到。

并且一旦它被发掘，他就被设置成灰色，我们的算法就不会再探索它，也不会更新它的所有属性。所以算法结束后每个节点的d属性也是正好等于它的深度，或者说所经过的节点数。

如果还不理解不妨自己在纸上画个两笔。

打印最短路径

通过上面的经验，我们知道广度优先搜索的搜索结果就是最短路径了，所以对于u，想要找到它和s节点的最短路径，只需要不停的找u的前驱节点直到找到s就好了。对于任意的节点也是。

这些前驱节点的数据全都存在那个search对象里。所以我们编写如下方法打印最短路径。

def path(s,u,v):
    if u == v:
        print(u)
    elif s.PI[v] == None:
        print("No path from %d to %d exists" % (u,v))
    else:
        path(s,u,s.PI[v])
        print(v)

g = Graph.SampleGraph()
s = Search(g)
bfs(g,s,0)
path(s,0,4)

对于疏通图，广度优先搜索的搜索结果构成一颗广度优先树。

广度优先搜索时间分析

我们可以通过算法看出，算法不会给任何节点涂白色，也就是说每个节点入队列和出队列都是一次，所以对队列的操作时间是O(V)，V是图中节点个数。算法会对每个邻接表最多扫描一次，所有邻接表的长度就是图中边的条数，记作E，所以总的复杂度是O(V+E)

深度优先搜索

如果说广度优先搜索像警察搜捕逃犯，那么深度优先搜索就像个专一的人，它喜欢“一条路走到黑”。没错，它只要认准了一条路就会一直走下去，直到自己和字节点都被标记为黑色。

深度优先搜索的颜色标记条件和广度优先搜索稍有不同，我们把未被探索的节点标记为白色，把已经探索的节点标记为灰色，把已经探索并且所有字节点也都已探索的节点标记为黑色。

除了颜色的定义不太一样，对于属性d的定义也不太一样，广度优先搜索中把d作为与源节点的距离，深度优先搜索把它作为节点被发现的时间。并且还引入了属性f，它是节点中的所有子节点都被探索完的时间。时间默认为0，每次记录时间时加1。

也就是说，节点被标记为灰色的那一刻，d属性被记录，被标记为黑色的那一刻，节点的f属性被记录。

编写代码：

from graph import Graph
from search import Search,WHITE,BLACK,GRAY

# 全局变量time 用于记录时间
time = 0

def dfs(G,C):
    for u in G.vertices():
        if C.color[u] == WHITE:
            dfs_visit(G,C,u)

def dfs_visit(G,C,u):
    global time
    time = time + 1
    C.d[u] = time
    C.color[u] = GRAY
    for v in G.Adj(u):
        if C.color[v] == WHITE:
            C.PI[v] = u
            dfs_visit(G,C,v)
    C.color[u] = BLACK
    time = time + 1
    C.f[u] = time


g = Graph.SampleGraph()
s = Search(g)
dfs(g,s)

看代码，我们在dfs方法中遍历了图中每个节点，对他调用dfs-visit方法，注意，当前节点很有可能在对其他节点调用dfs-visit方法时就已经被探索了，这是不用对他调用dfs-visit了，所以我们用一个if判断它是否被探索。

在dfs-visit中对节点u进行探索，首先要做的就是更新time，更新d属性和颜色，然后遍历所有u的直接连接节点，设置前驱节点并再次对它调用dfs-visit进行探索。这就产生了递归调用，这样就达到了沿着边一直深入的效果。

最后三行，是当u的连接的每个节点都被探索后，对u进行的设置，设置颜色和f属性。

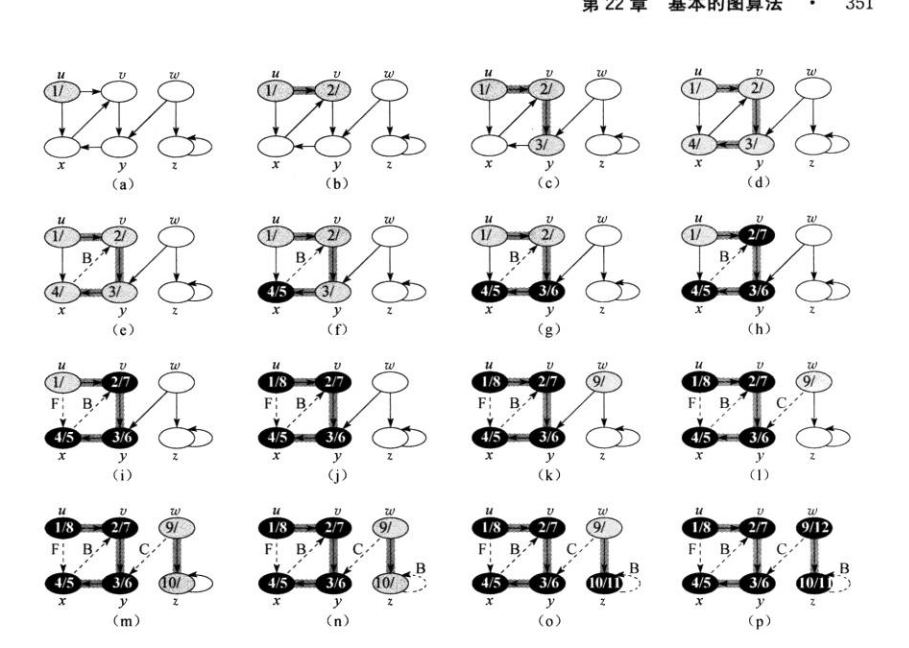
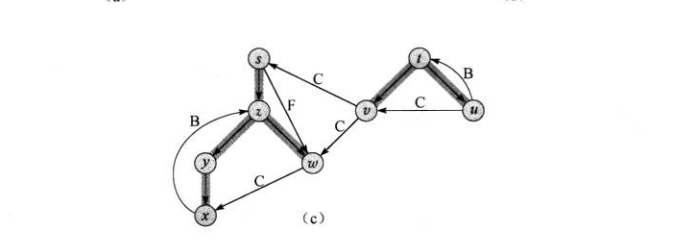
这是dfs在有向图上的运行过程。

深度优先搜索性质

1. 广度优先搜索会构成一个广度优先树，但是深度优先搜索不一定，它可能构成的是一个森林，而不仅仅是一整棵树。这是递归调用造成的，只要在dfs中调用的dfs-visit返回到dfs中，就会产生一个新的树。
2. v是深度优先森林里u的后代当且仅当节点v在节点u为灰色的时间段里被发现。
3. 节点发现时间具有括号化结构（同2）图片描述如下
   
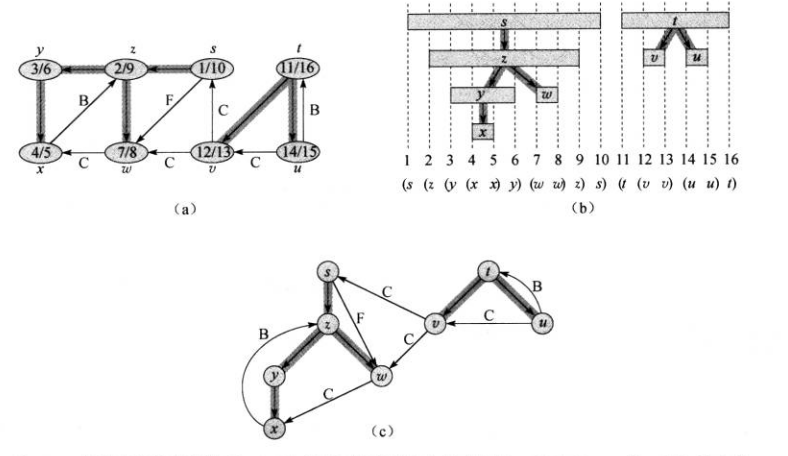
4. 对于图中任意两个节点u v来说，下面三种情况只可能有一种成立：
   1. 区间[u.d,u.f]和区间[v.d,v.f]完全分离，代表u v不在同一颗搜索树上
   2. 区间[u.d,u.f]完全包含在区间[v.d,v.f]中，代表u v在同一颗搜索树上且u是v的子节点
   3. 区间[v.d,v.f]完全包含在区间[u.d,u.f]中，代表u v在同一颗搜索树上且v是u的子节点
5. 在G的深度优先森林中，v是u的真后代当且仅当u.d<v.d<v.f<u.f时成立
6. 在G的深度优先森林中，v是u的后代当且仅当在发现节点u的时间u.d时，存在一条从节点u到v的全部由白色节点所构成的路径

如上性质很自然就能看出来，当然详细的论证见算法导论。

深度优先搜索时间分析

对每个节点调用dfs_visit的次数是1，因为只有白色节点可以调用，所以总共是V次，然后dfs-visit中对邻接表的所有边遍历，最大情况下也是E次，和广度优先一样，所以复杂度也是O(V+E)

深度优先搜索森林的几种边

我们可以通过搜索对深度优先森林的边进行分类。

1. 树边：如果节点v是因为算法对边(u,v)的探索而被发现，则(u,v)是一条树边。也就是说对边(u,v)探索时，节点v是白色
2. 后向边：后向边(u,v)是将节点u连接在其在深度优先树上的祖先节点v的边。自循环是特殊的后向边。当对(u,v)进行探索时，节点v是灰色
3. 前向边：后向边(u,v)是将节点u连接在其在深度优先树上的后代节点v的边。当对(u,v)进行探索时，节点v是黑色
4. 横向边：其他的边，这些边可能连通同一颗深度优先树中没有先后代关系的或者不是同一颗树中的节点。

下图标注了树中的各种边：

拓扑排序

拓扑排序只针对有向无环图

拓扑排序就是图G中所有节点的一种线性次序，在该次序中，如果包含边(u,v)那么u肯定在v前面。所以有环图是不可能排出一个线性序列的。

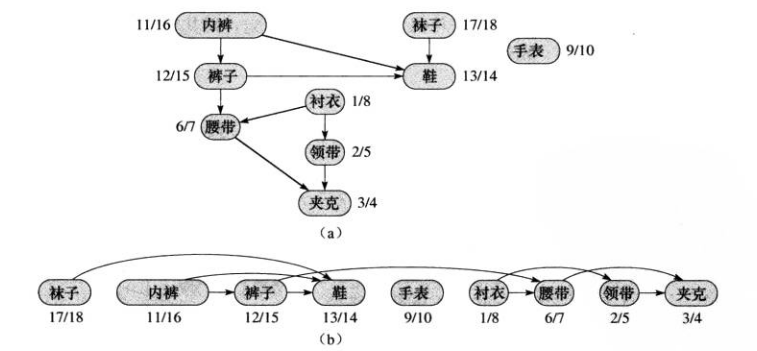
下图描述了Bumstead教授早上穿衣服的次序图。和线性序列。

对于有些衣服，他必按照先后顺序穿，有些则不需要。

从拓扑排序的定义可以看出它恰好符合深度优先搜索的搜索顺序，所以我们很轻易的就能写出拓扑排序算法。

算法导论里给的伪代码是这样的

TOPOLOGICAL-SORT(G)
    call DFS(G) to compute finishing times v.f for each vertex v
    as each vertex is finished, insert it onto the front of a linked list
    return the linked list of vertices

但是这样就要在dfs代码中添加新的插入链表的逻辑，或者为算法重新编写一个方法，并复制dfs的所有逻辑。我没有这样实现，我选择了依赖v.f进行排序

def sort(C):                                                                    
    result = list(zip(C.f.values(),C.f.keys()))
    result.sort()
    linkedList = []
    for i in result:
        linkedList.insert(0,i[1])
    print(linkedList)

不过受限于我们之前选择字典为数据结构的限制，这显然不是个好代码。sort方法中第一行我们把C里面记录f的字典转换为元组列表，并让节点的结束时间在前，节点本身在后，然后进行排序。python默认会按照元组中第一个元素升序排序，也就是按结束时间升序排序，这样就是图的线性排序了。

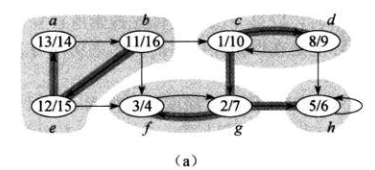
强连通分量

如上图，每个阴影是一个有向图的强连通分量，强连通分量中的每个节点可以互相到达。

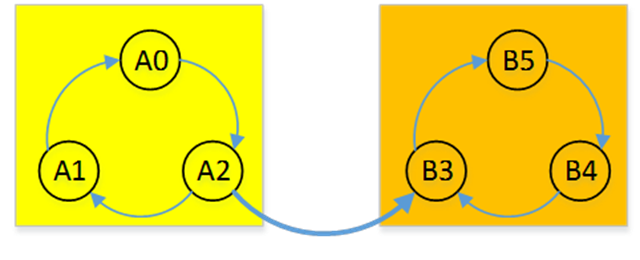
如何寻找有向图的强连通分量呢？我们采用Kosaraju算法求解。

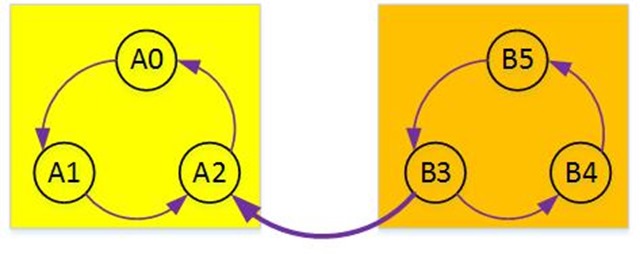
如上有一个图结构，我们可以很轻易的看出图中有两个强连通分量，A0-A1-A2是一个，B5-B4-B3又是一个。

那么算法怎么知道呢？假设我们对此图进行深度优先搜索，假如我们是从B5开始搜索的，那么算法会依次寻找B4、B3，然后算法会发现没有一条边能让我到达A那边，所以就会另外找一个未被探索的白色节点继续探索，目前A那边全是白色，并且那边全部连通，所以一次探索可以走完整副图。这样，我们两次选择的节点所能够连通的节点构成的子图就是该图的所有强连通分量。

但是事情并不都是那么巧的，假设我们从A那边选第一个节点，那一次就能走完整副图，这是算法酒并不能发现该图的所有强连通分量。

嘶，，我们发现只要率先选择B那边的任意一个节点就能找到所有强连通子图，那么我们怎么保证这个顺序呢？

kosaraju发明了一个算法，先对图G取反，记作G^T。取反就是原有向图G有边(u,v)，它取反的图就有一条边(v,u)。所以上图取反就是这样

取反后从任意一顶点逆后续进行DFS遍历，逆后续就是当这个节点的所有连通节点都探索完毕再将该节点记录到一个栈中。

这样得还如果先是取得A那边的节点，那么在图G^T中，它势必无法连通到B那边，所以还要单独取B那边的节点，这样，DFS完成后，记录节点的栈顶肯定是B那边的。

如果先取的是B那边的节点，一次能走完G^T，那么栈顶还是B那边的节点。这样就保证了我们要的顺序。

得到了这个顺序后，我们按这个顺序对原图进行DFS就可以了。一次DFS遍历中访问的所有定点都属于同一连通分量。

实现：

这个代码已经写的很凌乱了，哈哈哈哈哈哈。

from graph import Graph
from search import Search,WHITE,BLACK,GRAY

# 记录节点遍历顺序的栈
nodes = []
# 记录强连通分量的字典
cc = {}
time = 0
# 记录当前是否是逆后续遍历
inverse = False

# 修改过的特定dfs算法
def dfs(G,C):
    global nodes
    # 因为要更新nodes，所以单独弄一个变量复制nodes，把nodes清空
    vs = nodes
    nodes = []
    for u in vs:
        if C.color[u] == WHITE:
            # 如果不是逆后续 说明是第二次对原图遍历 这时需要记录强连通分量 这句是初始化和u一起的强连通分量列表
            if not inverse:
                cc[u] = []
            dfs_visit(G,C,u,u)

def dfs_visit(G,C,u,initialU):
    global time
    time = time + 1
    C.d[u] = time
    C.color[u] = GRAY
    for v in G.Adj(u):
        if C.color[v] == WHITE:
            # 记录强连通分量
            if not inverse:
                cc[initialU].append(v)
            C.PI[v] = u
            dfs_visit(G,C,v,u)
    C.color[u] = BLACK
    time = time + 1
    C.f[u] = time
    # 如果是逆后续，说明是第一次对逆图遍历，那么在节点的所有能到达的边都探索完成后 记录节点
    if inverse:
        nodes.insert(0,u)

## 求逆图
def reverse(G):
    GT = Graph(G.vertices())
    for u in G.vertices():
        for v in G.Adj(u):
            GT.connect(v,u)
    return GT

## 求强连通分量
def connected_component(G):
    global inverse
    GT = reverse(G)
    inverse = True
    dfs(GT,Search(G))
    inverse = False
    print(nodes)
    dfs(G,Search(G))


g = Graph.SampleGraphCC()
nodes = list(g.vertices())
connected_component(g)
print(cc)

同时添加了Graph类的SampleGraphCC方法，返回一个用于测试的图，此图就是上面演示的图只不过节点换成了数字：

@staticmethod
def SampleGraphCC():
    g = Graph([1,2,3,4,5,6])
    g.connect(1,2)
    g.connect(2,3)
    g.connect(3,1)
    g.connect(3,4)
    g.connect(4,5)
    g.connect(5,6)
    g.connect(6,4)
    return g

参考资料

• 算法导论 第三版 图算法 Thomas H. Cormen 等
• Kosaraju算法解析: 求解图的强连通分量 nullzx

如有错误敬请指正！