python数据分析与算法之五算法

5.1线性回归算法模型

机器学习

人工智能和机器学习之间的关系
- 机器学习是实现人工智能的一种技术手段
算法模型
- 概念：特殊对象。该对象内部封装了某种还没有求出解的方程！
- 作用：
  - 预测：天气预报
  - 分类：将一个未知分类的事务归属到某一种已知的分类中。
- 算法模型对象内部封装的方程的解就是算法模型预测或则分类的结果
样本数据
- 样本数据和算法模型之间的关系是什么？
  - 模型的训练：需要将样本数据带入到模型对象中，让模型对象的方程求出解。
- 什么是样本数据？样本数据是由什么构成的？
  - 特征数据：自变量。往往是有多种特征组成
  - 目标数据：因变量
- 算法模型的分类：
  - 有监督学习：
    - 如果算法模型对象需要的样本数据必须有目标数据和特征数据
  - 无监督学习：
    - 如果算法模型对象需要的样本数据只需要有特征数据即可
- sklearn模块中的模型

案例 : Sea distance

城市气候与海洋的关系研究

1.导入包

import numpy as np
import pandas as pd
from pandas import Series,DataFrame

import matplotlib.pyplot as plt
from pylab import mpl
mpl.rcParams['font.sans-serif'] = ['FangSong'] # 指定默认字体
mpl.rcParams['axes.unicode_minus'] = False # 解决保存图像是负号'-'显示为方块的问题

View Code

2.导入数据各个海滨城市数据

ferrara1 = pd.read_csv('./ferrara_150715.csv')
ferrara2 = pd.read_csv('./ferrara_250715.csv')
ferrara3 = pd.read_csv('./ferrara_270615.csv')
ferrara=pd.concat([ferrara1,ferrara1,ferrara1],ignore_index=True)

torino1 = pd.read_csv('./torino_150715.csv')
torino2 = pd.read_csv('./torino_250715.csv')
torino3 = pd.read_csv('./torino_270615.csv')
torino = pd.concat([torino1,torino2,torino3],ignore_index=True) 

mantova1 = pd.read_csv('./mantova_150715.csv')
mantova2 = pd.read_csv('./mantova_250715.csv')
mantova3 = pd.read_csv('./mantova_270615.csv')
mantova = pd.concat([mantova1,mantova2,mantova3],ignore_index=True) 

milano1 = pd.read_csv('./milano_150715.csv')
milano2 = pd.read_csv('./milano_250715.csv')
milano3 = pd.read_csv('./milano_270615.csv')
milano = pd.concat([milano1,milano2,milano3],ignore_index=True) 

ravenna1 = pd.read_csv('./ravenna_150715.csv')
ravenna2 = pd.read_csv('./ravenna_250715.csv')
ravenna3 = pd.read_csv('./ravenna_270615.csv')
ravenna = pd.concat([ravenna1,ravenna2,ravenna3],ignore_index=True)

asti1 = pd.read_csv('./asti_150715.csv')
asti2 = pd.read_csv('./asti_250715.csv')
asti3 = pd.read_csv('./asti_270615.csv')
asti = pd.concat([asti1,asti2,asti3],ignore_index=True)

bologna1 = pd.read_csv('./bologna_150715.csv')
bologna2 = pd.read_csv('./bologna_250715.csv')
bologna3 = pd.read_csv('./bologna_270615.csv')
bologna = pd.concat([bologna1,bologna2,bologna3],ignore_index=True)

piacenza1 = pd.read_csv('./piacenza_150715.csv')
piacenza2 = pd.read_csv('./piacenza_250715.csv')
piacenza3 = pd.read_csv('./piacenza_270615.csv')
piacenza = pd.concat([piacenza1,piacenza2,piacenza3],ignore_index=True)

cesena1 = pd.read_csv('./cesena_150715.csv')
cesena2 = pd.read_csv('./cesena_250715.csv')
cesena3 = pd.read_csv('./cesena_270615.csv')
cesena = pd.concat([cesena1,cesena2,cesena3],ignore_index=True)

faenza1 = pd.read_csv('./faenza_150715.csv')
faenza2 = pd.read_csv('./faenza_250715.csv')
faenza3 = pd.read_csv('./faenza_270615.csv')
faenza = pd.concat([faenza1,faenza2,faenza3],ignore_index=True)

View Code

3.去除没用的列

city_list = [faenza,cesena,piacenza,bologna,asti,ravenna,milano,mantova,torino,ferrara]
for city in city_list:
    city.drop(labels='Unnamed: 0',axis=1,inplace=True)
    
faenza.head()

View Code

4.显示最高温度于离海远近的关系（观察多个城市）

max_temp = []
dist_list = []
for city in city_list:
    temp = city['temp'].max()
    max_temp.append(temp)
    dist = city['dist'][0]
    dist_list.append(dist)
max_temp
dist_list

View Code

散点图的绘制

plt.scatter(dist_list,max_temp)    # plt.scatter(x,y) 
plt.xlabel('距离')
plt.ylabel('最高温度')
plt.title('最高温度和距离直接的关系')

View Code

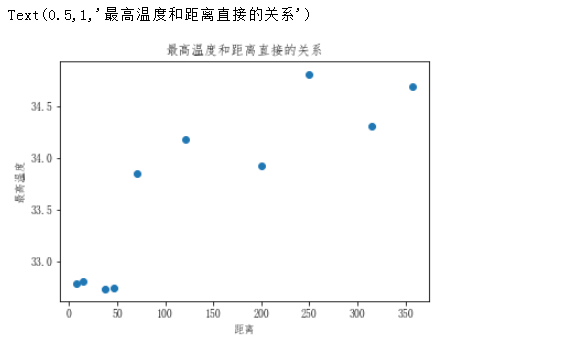
线形图的绘制

plt.plot(dist_list,max_temp)
plt.xlabel('距离')
plt.ylabel('最高温度')
plt.title('最高温度和距离直接的关系')

View Code

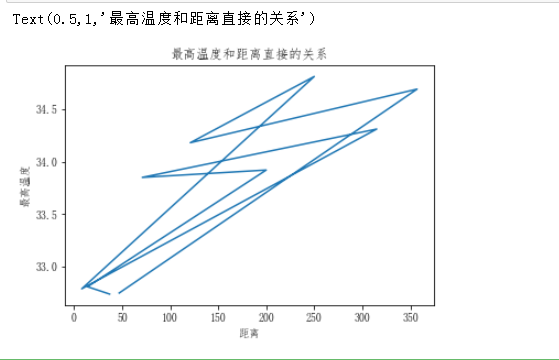
需要我们建立一个温度模型，让其可以根据一个距离预测吃该距离对应城市的最高温度是多少

#线性回归算法模型 y = wx + b  ==> y = 3x + 5
from sklearn.linear_model import LinearRegression
linner = LinearRegression() #算法模型对象

#样本数据的提取
feature = np.array(dist_list) #数组形式的特征数据
target = np.array(max_temp)   #数组形式的目标数据
feature.shape

View Code

#训练模型
linner.fit(feature.reshape(-1,1),target) # X表示特征数据必须是二维的！！！
#基于训练好的模型对象实现预测功能（获取方程的解）
linner.predict([[266],[333]])

View Code

x = np.linspace(0,400,num=100)
y = linner.predict(x.reshape(-1,1))

plt.scatter(dist_list,max_temp)
plt.scatter(x,y)
plt.xlabel('距离')
plt.ylabel('最高温度')
plt.title('最高温度和距离直接的关系')

View Code

5.2KNN算法模型

5.2.1k-近邻算法原理

简单地说，K-近邻算法采用测量不同特征值之间的距离方法进行分类（k-Nearest Neighbor，KNN）
- 优点：精度高、对异常值不敏感、无数据输入假定。
- 缺点：时间复杂度高、空间复杂度高。
  - 1、当样本不平衡时，比如一个类的样本容量很大，其他类的样本容量很小，输入一个样本的时候，K个临近值中大多数都是大样本容量的那个类，这时可能就会导致分类错误。改进方法是对K临近点进行加权，也就是距离近的点的权值大，距离远的点权值小。
  - 2、计算量较大，每个待分类的样本都要计算它到全部点的距离，根据距离排序才能求得K个临近点，改进方法是：先对已知样本点进行剪辑，事先去除对分类作用不大的样本。
- 适用数据范围：数值型和标称型标称型：标称型目标变量的结果只在有限目标集中取值，如真与假(标称型目标变量主要用于分类) 数值型：数值型目标变量则可以从无限的数值集合中取值，如0.100，42.001等 (数值型目标变量主要用于回归分析)

工作原理

训练样本集
- 存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每一数据与所属分类的对应关系。输人没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，我们只选择样本数据集中前K个最相似的数据，这就是K-近邻算法中K的出处,通常K是不大于20的整数。最后，选择K个最相似数据中出现次数最多的分类，作为新数据的分类。
电影类别KNN分析

欧几里得距离(Euclidean Distance)
计算过程图

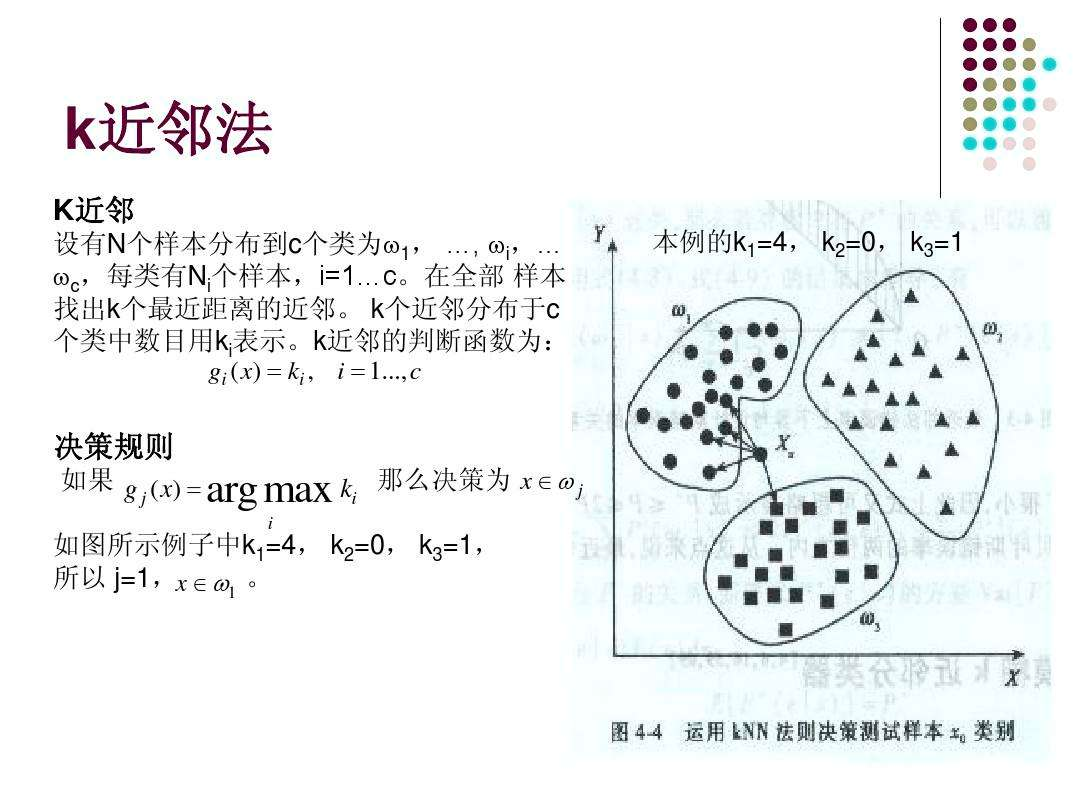
kNN近邻分类算法的原理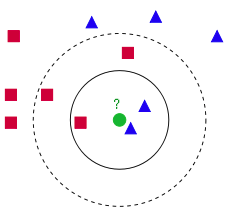

从上图中我们可以看到，图中的数据集都有了自己的标签，一类是蓝色的正方形，一类是红色的三角形，那个绿色的圆形是我们待分类的数据
如果K=3，那么离绿色点最近的有2个红色三角形和1个蓝色的正方形，这3个点投票，于是绿色的这个待分类点属于红色的三角形.
如果K=5，那么离绿色点最近的有2个红色三角形和3个蓝色的正方形，这5个点投票，于是绿色的这个待分类点属于蓝色的正方形
我们可以看到，KNN本质是基于一种数据统计的方法！其实很多机器学习算法也是基于数据统计的
总结
- KNN是一种基于记忆的学习(memory-based learning)，也是基于实例的学习(instance-based learning)，属于惰性学习(lazy learning)。即它没有明显的前期训练过程，而是程序开始运行时，把数据集加载到内存后，不需要进行训练，就可以开始分类了。

5.2.2案例:电影分类

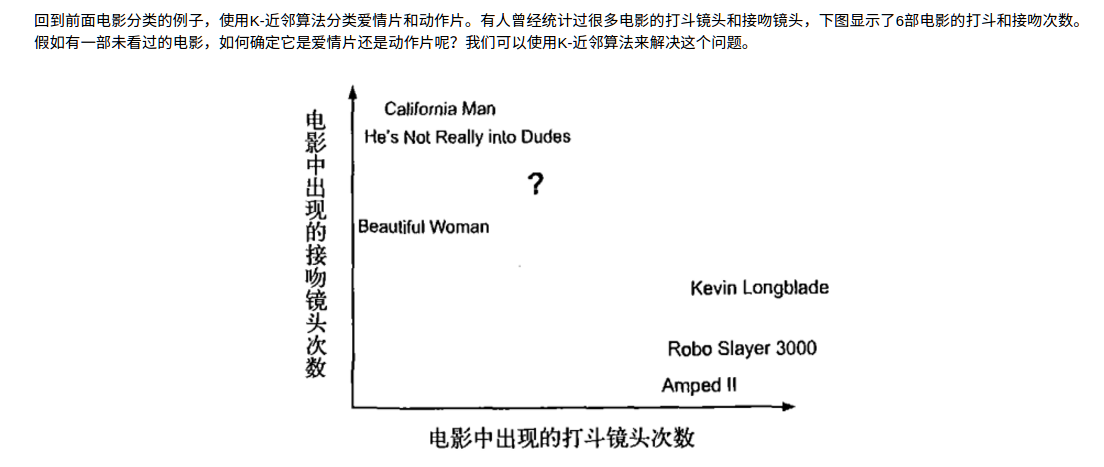
有人曾经统计过很多电影的打斗镜头和接吻镜头，下图显示了6部电影的打斗和接吻次数。假如有一部未看过的电影，如何确定它是爱情片还是动作片呢？我们可以使用K-近邻算法来解决这个问题。

首先我们需要知道这个未知电影存在多少个打斗镜头和接吻镜头，上图中问号位置是该未知电影出现的镜头数图形化展示，具体数字参见下表。

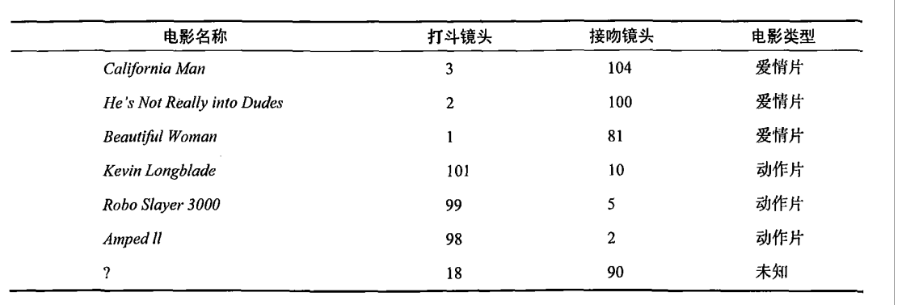
即使不知道未知电影属于哪种类型，我们也可以通过某种方法计算出来。首先计算未知电影与样本集中其他电影的距离，如图所示。

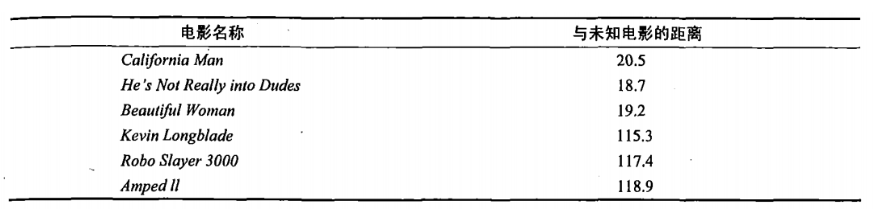
现在我们得到了样本集中所有电影与未知电影的距离，按照距离递增排序，可以找到K个距离最近的电影。假定k=3，则三个最靠近的电影依次是California Man、He's Not Really into Dudes、Beautiful Woman。K-近邻算法按照距离最近的三部电影的类型，决定未知电影的类型，而这三部电影全是爱情片，因此我们判定未知电影是爱情片。

5.2.3在scikit-learn库中使用k-近邻算法

import pandas as pd
df = pd.read_excel('../../my_films.xlsx')
df


feature = df[['Action lens','Love lens']]
target = df['target']
from sklearn.neighbors import KNeighborsClassifier
knn = KNeighborsClassifier(n_neighbors=2)    #导出未知事物周围三个数据
knn.fit(feature,target)
knn.score(feature,target)    # 给n_neighbors=2 打分


knn.predict([[60,50]])

View Code

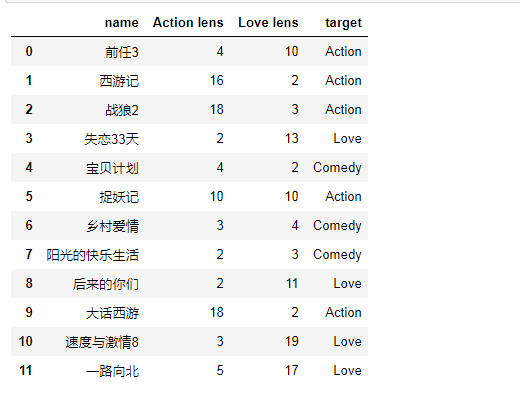
用于分类

import sklearn.datasets as datasets   #提供大量基于机械学习样本数据
datasets.load_iris()

View Code

预测年收入是否大于50K美元

数据的读取

df = pd.read_csv('../data/adults.txt')
df.head(1)

View Code

获取年龄、教育程度、职位、每周工作时间作为机器学习数据 ,获取薪水作为对应结果

feature = df[['age','education_num','occupation','hours_per_week']]
target = df['salary']
occ_arr = feature['occupation'].unique()
dic = {}
for i in range(occ_arr.size):
    dic[occ_arr[i]] = i
feature['occupation'] = feature['occupation'].map(dic)
feature.head()

View Code

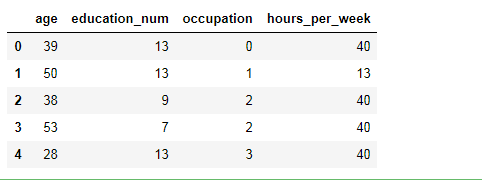
切片：训练数据和预测数据 32560

#训练数据：负责模型的训练
x_train = feature[0:32500]
y_train = target[0:32500]
#测试数据：负责测试模型的精准度
x_test = feature[32500:]
y_test = target[32500:]

View Code

实例化模型

knn = KNeighborsClassifier(n_neighbors=20)
knn.fit(x_train,y_train)
knn.score(x_train,y_train)

View Code

测试精准度

print('模型的分类结果：',knn.predict(x_test))
print('真实的分类结果：',y_test)

View Code

测试
```
knn.predict([[45,13,4,50]])
```
View Code

5.2.4KNN手写数字识别

手写数字是一张图片,让knn模型将图片中的数据识别出来

包的导入

import numpy as np
import matplotlib .pyplot as plt 
from sklearn.neighbors import KNeighborsClassifier

View Code

图片的导入

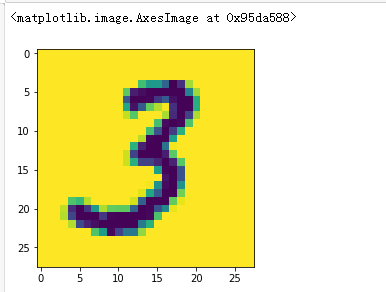
img_arr = plt.imread('./data/3/3_33.bmp')
img_arr.shape

View Code

plt.imshow(img_arr)

View Code

提取样本数据

feature = []   #样本数据
target = []    #目标数据
for i in range(10):
    for j in range(1,501):   #data/3/3_33.bmp
        imgPath = './data/'+str(i)+'/'+str(i)+'_'+str(j)+'.bmp'
        img_arr = plt.imread(imgPath)
        feature.append(img_arr)
        target.append(i)

View Code

将列表形式的样本转成数组形式的

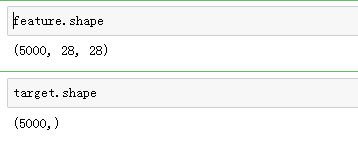
feature = np.array(feature)
target = np.array(target)

View Code

将三维数组变成二维

feature = feature.reshape((5000,784))
feature.shape

View Code

对样本数据进行打乱

np.random.seed(10)
np.random.shuffle(feature)
np.random.seed(10)
np.random.shuffle(target)

View Code

拆分训练数据和测试数据

x_train = feature[0:4980]
y_train = target[0:4980]
                 
x_test = feature[4980:]
y_test = target[4980:]

View Code

训练模型

knn = KNeighborsClassifier(n_neighbors = 17 )
knn.fit(x_train,y_train)

print('模型分类的结果:',knn.predict(x_test))
print('真实是分类结果:',y_test)

View Code

将训练好的模型进行保存

from sklearn.externals import joblib
joblib.dump(knn,'./knn_1.n')

View Code

加载保存好的模型

#加载保存好的模型
knn = joblib.load('./knn_1.n')

View Code

让模型识别外部图片

ex_img_arr = plt.imread('./数字.jpg')
plt.imshow(ex_img_arr)

View Code

图片的裁剪

#将4的区域局部裁剪
img_4_arr = ex_img_arr[100:160,0:60,:]

img_4_arr
plt.imshow(img_4_arr)

View Code

降维度

img_4_arr = img_4_arr.mean(axis=2)
img_4_arr.shape

View Code

像素的等比压缩

import scipy.ndimage as ndimage
eight = ndimage.zoom(img_4_arr,zoom=(28/60,28/60))
plt.imshow(eight)

View Code

5.3查找算法

5.3.1二分查找

有序列表对于我们的实现搜索是很有用的。在顺序查找中，当我们与第一个元素进行比较时，如果第一个元素不是我们要查找的，则最多还有 n-1 个元素需要进行比较。二分查找则是从中间元素开始，而不是按顺序查找列表。如果该元素是我们正在寻找的元素，我们就完成了查找。如果它不是，我们可以使用列表的有序性质来消除剩余元素的一半。如果我们正在查找的元素大于中间元素，就可以消除中间元素以及比中间元素小的一半元素。如果该元素在列表中，肯定在大的那半部分。然后我们可以用大的半部分重复该过程，继续从中间元素开始，将其与我们正在寻找的内容进行比较。

def sort(alist,item): #item就是我们要找的元素
    low = 0 #进行二分查找操作的列表中第一个元素的下标
    high = len(alist)-1#进行二分查找操作的列表中最后一个元素的下标
    find = False
    
    while low <= high:
        mid = (low+high) // 2 #中间元素的下标
        if item > alist[mid]:#我们要找的数比中间元素值大，则意味着我们要找的数在中间元素的右侧
            low = mid + 1
        elif item < alist[mid]:#找的数比中间元素小，则意味着我们要找的数是在中间元素左侧
            high = mid - 1
        else:#找到啦
            find = True
            break
    return find
       
print(sort(alist,51))

View Code

5.4排序算法

5.4.1冒泡排序

1.将列表中的每两个列表元素进行大小比较,将两个元素中较大的数值逐步向后移动

def sort(alist):
    for j in range(0,len(alist)-1):
        
        for i in range(len(alist)-1-j):
            if alist[i] > alist[i+1]:
               alist[i],alist[i+1] = alist[i+1],alist[i]
    print(alist)
alist = [4,11,7,6,8,9]
sort(alist)

View Code

5.4.2选择排序

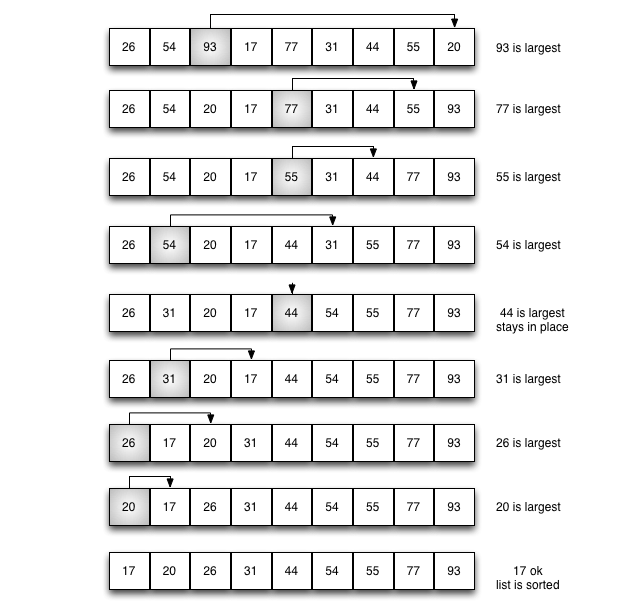
1.直接将列表中最大值找出,放在列表最后的位置

def sort(alist):
    max = 0 #max中存储的是列表中元素值最大数的下标,最开始先假设列表为0的元素为最大值
    for i in range(0,len(alist)-1):
        if alist[max] < alist[i+1]:
            max = i + 1
    #将最大值放在列表末尾的位置
    alist[max],alist[len(alist)-1] = alist[len(alist)-1],alist[max]
    print(alist)

View Code

def sort(alist):
    for j in range(len(alist)-1,0,-1):   #5,4,3,2,1
        max = 0    #max中存储的是列表中元素值最大数的下标,最开始先假设列表为0的元素为最大值 
        for i in range(0,j):   #len(alist)-1 ==> j
            if alist[max] < alist[i+1]:
                max = i + 1
        #将最大值放在列表末尾的位置
        alist[max],alist[j] = alist[j],alist[max]
    print(alist)

View Code

5.4.3插入排序

插入排序的主要思想是每次取一个列表元素与列表中已经排序好的列表段进行比较，然后插入从而得到新的排序好的列表段，最终获得排序好的列表。比如，待排序列表为[49,38,65,97,76,13,27,49]，则比较的步骤和得到的新列表如下：(带有背景颜色的列表段是已经排序好的，红色背景标记的是执行插入并且进行过交换的元素）

#step_1
i = 1 #i表示的是列表中左侧部分有序部分的数据个数,其次还需要让i充当列表的下标
if alist[i] < alist[i-1]:
    alist[i],alist[i-1] = alist[i-1],alist[i]
    i += 1
#step_2
i = 2
#alist[i] :乱序部分的第一个元素
#alist[i-1] :有序部分的第二个元素
while i >=1:
    if alist[i] < alist[i-1]:
        alist[i],alist[i-1] = alist[i-1],alist[i]
        i -= 1
    else:
        break
#step_3
for i in range(1,len(alist)+1):
    #alist[i] :乱序部分的第一个元素
    #alist[i-1] :有序部分的第二个元素
    while i >=1:
        if alist[i] < alist[i-1]:
            alist[i],alist[i-1] = alist[i-1],alist[i]
            i -= 1
        else:
            break
#完整版
def sort(alist):
    for i in range(1,len(alist)):
        #alist[i] :乱序部分的第一个元素
        #alist[i-1] :有序部分的第二个元素
        while i >= 1:
            if alist[i] < alist[i-1]:
                alist[i],alist[i-1] = alist[i-1],alist[i]
                i -= 1
            else:
                break
    print(alist)

View Code

5.4.4希尔排序

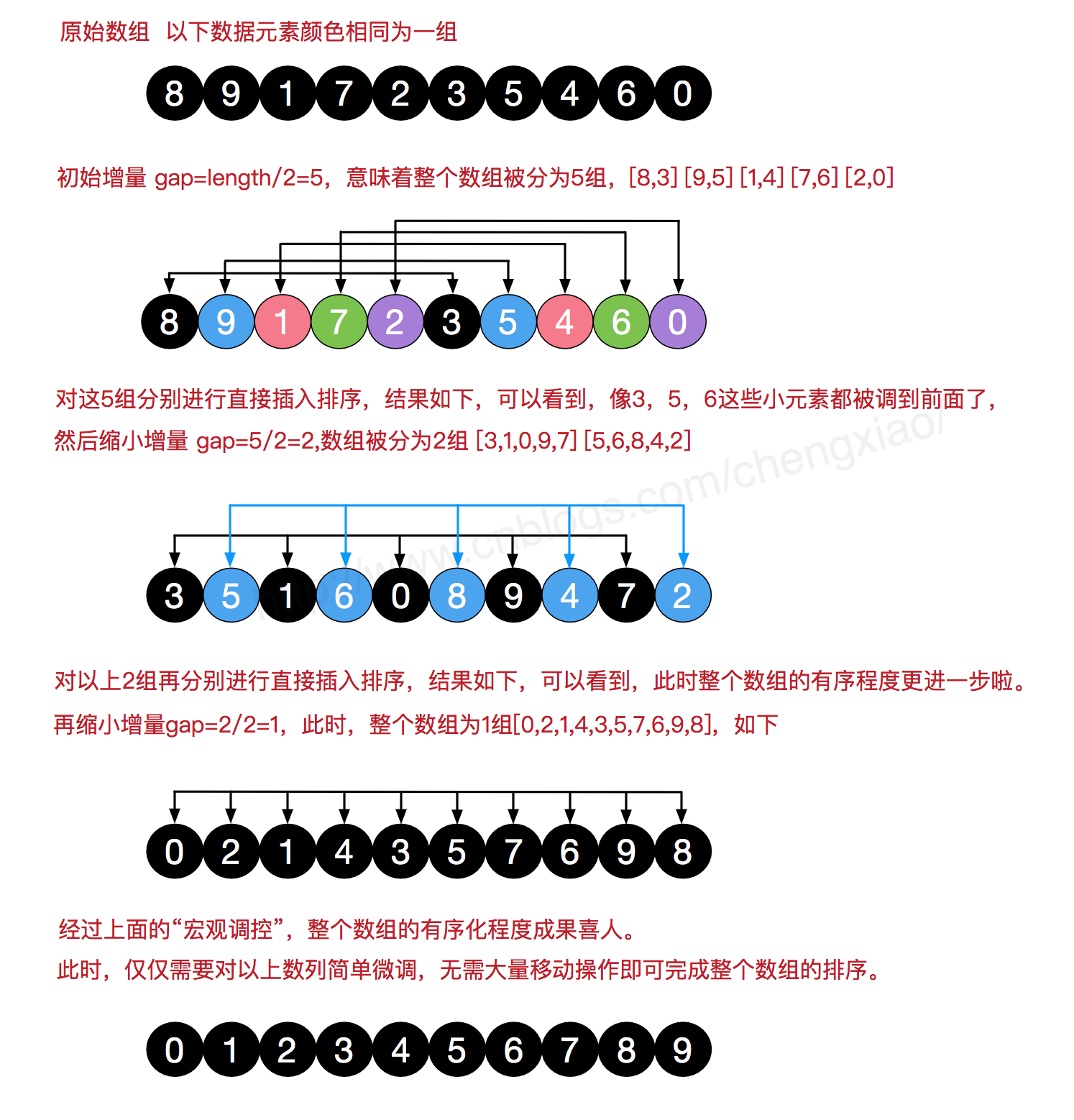
希尔排序(Shell Sort)是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本,

该方法的基本思想是：

先将整个待排元素序列分割成若干个子序列（由相隔某个“增量（gap）”的元素组成的）分别进行直接插入排序，
然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下（接近最好情况），效率是很高的，因此希尔排序在时间效率比直接插入排序有较大提高。

#step_1
def sort(alist):
    gap = len(alist) // 2
    #将插入排序当做增量为1的希尔排序
    for i range(1,len(alist)):
        while i > 0 :
            if alist[i] < alist[i-1]:
                alist[i],alist[i-1] = alist[i-1],alist[i]
                i -= 1
            else:
                break
##step_2
def sort(alist):
    gap = len(alist) // 2
    #将增量设置成gap
    for i range(gap,len(alist)):
        while i > 0 :
            if alist[i] < alist[i-gap]:
                alist[i],alist[i-gap] = alist[i-gap],alist[i]
                i -= gap
            else:
                break
#完整版
#继续缩小增量
def sort(alist):
    gap = len(alist) // 2
    while gap >= 1:
        #将增量设置成gap
        for i in range(gap,len(alist)):
            while i > 0 :
                if alist[i] < alist[i-gap]:
                    alist[i],alist[i-gap] = alist[i-gap],alist[i]
                    i -= gap
                else:
                    break
        gap //= 2
    return alist

View Code

5.4.5快速排序

将列表中第一个元素设定为基准数字，赋值给mid变量，然后将整个列表中比基准小的数值放在基准的左侧，比基准到的数字放在基准右侧。然后将基准数字左右两侧的序列在根据此方法进行排放。
定义两个指针，low指向最左侧，high指向最右侧
然后对最右侧指针进行向左移动，移动法则是，如果指针指向的数值比基准小，则将指针指向的数字移动到基准数字原始的位置，否则继续移动指针。
如果最右侧指针指向的数值移动到基准位置时，开始移动最左侧指针，将其向右移动，如果该指针指向的数值大于基准则将该数值移动到最右侧指针指向的位置，然后停止移动。

如果左右侧指针重复则，将基准放入左右指针重复的位置，则基准左侧为比其小的数值，右侧为比其大的数值。

#第一次排序：将将比基准小的排列在基准左侧，def sort(alist):
def sort(alist):
    low = 0
    high = len(alist)-1
    #基准：最左侧的数值
    mid = alist[low]
    #low和high的关系只能是小于，当等于的时候就要填充mid了
    while low < high:
        while low < high:
            if alist[high] > mid:
                high -= 1
            else:
                alist[low] = alist[high]
                break
        while low < high:
            if alist[low] < mid:
                low += 1
            else:
                alist[high] = alist[low]
                break
        
        #当low和high重复的时候，将mid填充
        if low == high:
            alist[low] = mid #or alist[high] = mid  
            break
    return alist
#完整版
def sort(alist,start,end):
    low = start
    high = end
    #递归结束的条件
    if low > high:
        return
    #基准：最左侧的数值
    mid = alist[low]
    #low和high的关系只能是小于，当等于的时候就要填充mid了
    while low < high:
        while low < high:
            if alist[high] > mid:
                high -= 1
            else:
                alist[low] = alist[high]
                break
        while low < high:
            if alist[low] < mid:
                low += 1
            else:
                alist[high] = alist[low]
                break
        
        #当low和high重复的时候，将mid填充
        if low == high:
            alist[low] = mid #or alist[high] = mid  
            break
    #执行左侧序列
    sort(alist,start,high-1)
    #执行右侧序列
    sort(alist,low+1,end)
    
    return alist

View Code

posted @ 2019-09-10 16:20 Primrose 阅读(1596) 评论(0) 编辑收藏举报

刷新页面返回顶部

Primrose

python数据分析与算法之五 算法

机器学习

案例 : Sea distance

散点图的绘制

线形图的绘制

5.2KNN算法模型

5.2.1k-近邻算法原理

工作原理

kNN近邻分类算法的原理

5.2.2案例:电影分类

5.2.3在scikit-learn库中使用k-近邻算法

用于分类

预测年收入是否大于50K美元

5.2.4KNN手写数字识别

5.3查找算法

5.3.1二分查找

5.4排序算法

5.4.1冒泡排序

5.4.2选择排序

5.4.3插入排序

5.4.4希尔排序

5.4.5快速排序

公告

python数据分析与算法之五算法