数据结构与算法小结——排序(七)
4. 归并排序
4.1 递归实现
函数的递归本质上是一个压栈出栈的过程,更广意义上来说,函数调用都是压栈和出栈的过程,排序这一系列完了 ,我打算写一下函数调用和栈的关系的一章,看看能不能把这个过程理解透彻一些。
具体来说归并排序的递归实现。其主要思想是把待排序序列分为大小基本相同的两个部分,分别对前后两个部分进行同样的操作,调用自身不断压栈。到最后一层只有一个元素后,栈空间弹出栈顶元素,按照原先的切割部位,进行merge操作,见图 1。
merge操作是用i、j两个变量来循环前一段元素和后一段元素,一个一个比较,小的就依次放在新排好的序列中,i(或j)+1,继续往后比。最后剩余的元素一次性接在已排好序的元素后面即可,图示见图 2。非递归的merge比较简单,按照压栈时的切割部位合并即可,不会出现还有剩余的段没有办法merge的问题,非递归则会出现这种问题,详细可以见下一节。
前面在说快速排序的时候提到,快速排序用了递归,归并排序也用了递归,两者的区别是什么?区别在于快速排序做的是递归的前处理,即用pivotvalue让前小后大;递归的归并排序做的是递归的后处理,将切割后的元素用merge操作合并。
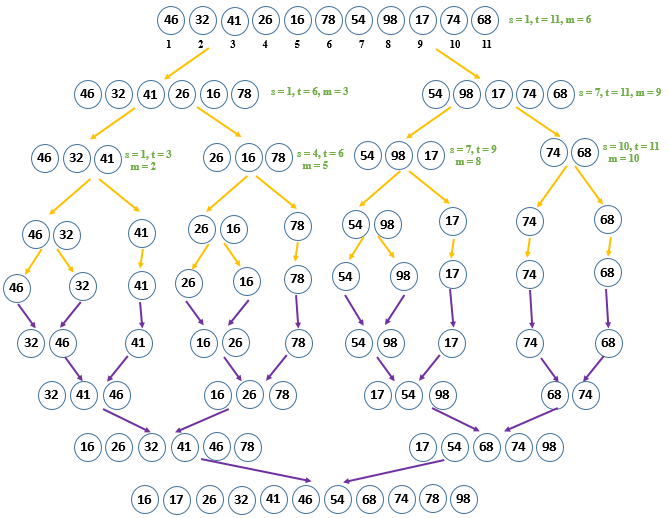
图 1 递归的归并排序
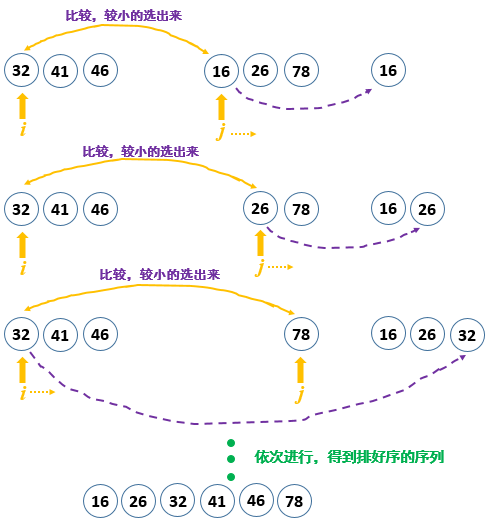
图 2 merge操作(递归的后处理操作)
分析递归的归并排序的时间复杂度,画出递归树可以发现,递归树是完全二叉树,所以其时间复杂度最好、最坏、平均都是O(nlgn)。
分析递归的归并排序的空间复杂度,由于用到了递归栈,所以会用到额外的O(lgn)的空间;另外,在排序时还会用到额外的O(n),所以其空间复杂度为O(n+lgn)。
归并排序还有一个优点是它是稳定的。
总结其时间、空间复杂度、稳定性和适用场合如图 3。
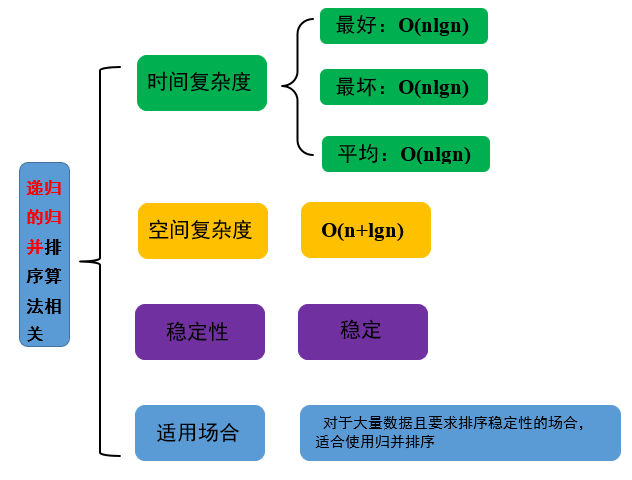
图 3 递归的归并排序相关

