数据结构与算法小结——排序（四）

2.2 堆排序

　　堆：1. 是完全二叉树；2. 树中所有结点都比左右孩子大（或小）。（但在实现过程发现，其实堆排序并没有用到树结构，还是用的顺序表，只是用完全二叉树来理解而已）。

　　堆排序是一种选择排序算法，其主要思路是：先将所有待排序元素构造成一个大顶堆（或小顶堆），接着将堆顶元素和最后一个元素（层序遍历）交换，就得到了这些元素里的最大值，接着将剩余元素继续构造大顶堆，交换得到次大值......依次循环，得到排好序的序列。

　　堆排序的思路很好理解，但关键点有两个：

　　1. 从无序元素到大顶堆的构造；

　　2. 交换并输出堆顶元素以后，如何调整剩余元素成为大顶堆。

　　首先说第一个：如何将无序元素构造成一个大顶堆。可以把这个步骤分成两个要点来看，第一个：找到所有的非叶结点，从下往上、从右往左循环，如图 1；第二个：对所有的非叶节点都进行选最大值的操作，这个操作对于小枝结点和大枝结点（自己定义的概念，如图 2所示）还有点区别。如果是小枝结点，则先比较左右孩子，再把其中的大值与小枝结点比较，如果小枝结点的值大，则不做操作，如果小，则互换小枝结点和值比较大的孩子结点即可（如图 3）；如果是大枝结点，那么在上面互换的基础上，对于和父节点交换了值的孩子结点，还要继续往下重复上面的过程，知道不交换或者到叶节点为止（如图 4）。

  

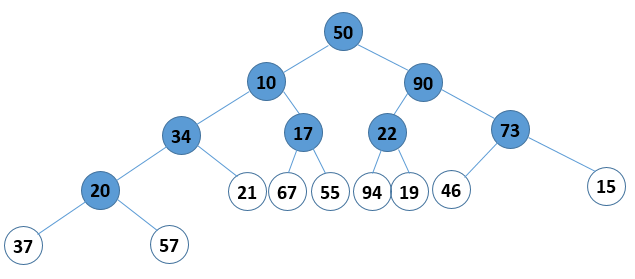
图 1 找到所有的非叶节点

 

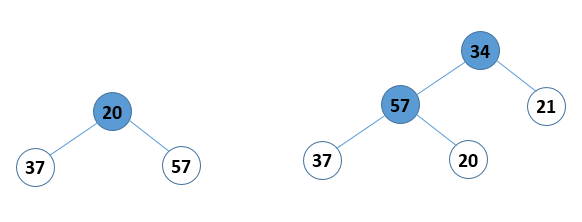
图 2 小枝结点和大枝结点

　　　　

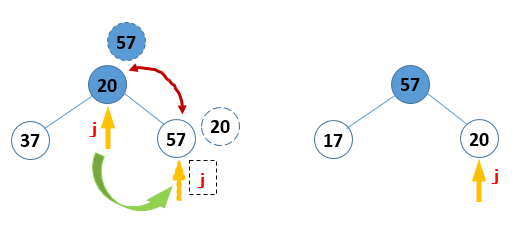
图 3 小枝结点的调整

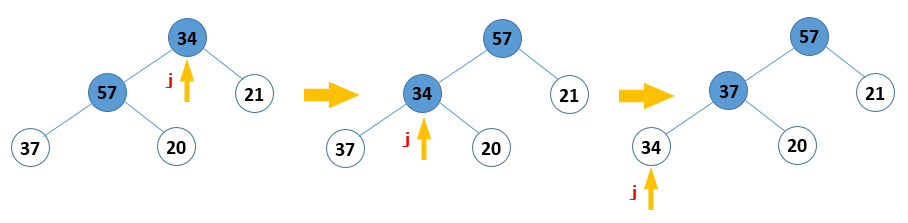
图 4 大枝结点的调整

 　　经过上面一直到根节点的循环，初始的大顶堆已经构造好，将堆顶元素和最后一个元素交换，即可得到待排序元素中最大的值。

　　接着，由于将最后一个元素提上去了，需要重新构造大顶堆。此时，由于大部分元素已经是大顶堆结构了，将新的堆顶元素按照上面所说的大枝结点的调整方式，即可得到新的大顶堆，交换进而得到次大元素......依次循环，得到排好序的序列。

　　可以看到，构造大顶堆时是按照从下往上、从右往左的顺序依次进行。可不可以从上往下，即从第一个元素开始呢？不行，因为从下往上的过程，将大部分元素都构造成了大顶堆，大枝结点调整其实只是走了一条路径，另外一条不处理的原因在于，那一条已经是构造好了的大顶堆结构。如果从第一个元素开始构造大顶堆，则不会满足这样的关系，无法得到预期结果。

　　大顶堆的构造很巧妙，它被归为选择排序的原因可能是因为，在做结点调整的时候，要选择三个结点中的最大值作为根节点吧。

　　再来看一下堆排序的时间、空间复杂度、稳定性以及适用场合：

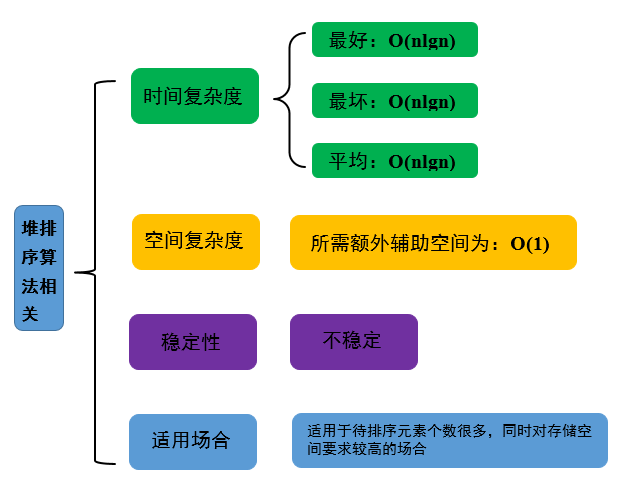
图 5 堆排序相关性能

　　可以看到，堆排序的时间复杂度为O(nlgn)，空间复杂度为O(1)，是就地排序。当待排序元素很多时，适合适用改进的排序算法，而若是同时对存储空间要求比较高，就比较适合适用堆排序算法了。

　　分析一下时间复杂度（图6）和稳定性（图7）：

　　

图 6 堆排序时间复杂度分析

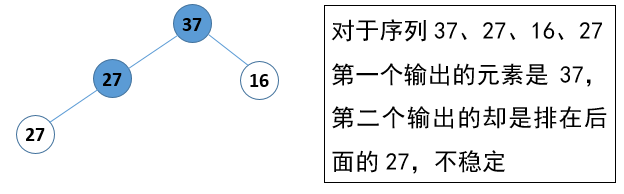
图 7 堆排序稳定性分析