初等函数

初等函数

初等函数（基本函数）是由常函数、幂函数、指数函数、对数函数、三角函数和反三角函数经过有限次的有理运算（加、减、乘、除、有限次乘方、有限次开方）及有限次函数复合所产生、并且在定义域上能用一个方程式表示的函数。

一般来说，分段函数不是初等函数，因为在这些分段函数的定义域上不能用一个解析式表示。

常函数

称{\displaystyle f(x)=C}f(x)=C为常数函数，其中C为常数，它的定义域为{\displaystyle (-\infty ,\infty )}{\displaystyle (-\infty ,\infty )}。
常函数'"`UNIQ--postMath-00000003-QINU`"'图像

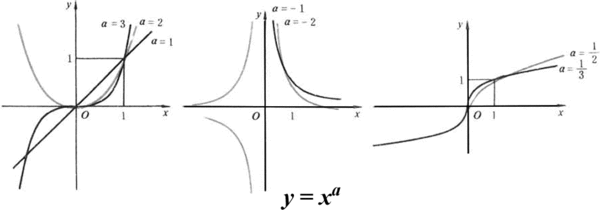
幂函数

称形如{\displaystyle f(x)=Cx^{r}}f(x)=Cx^{r}的函数为幂函数，其中C, r为常数。幂函数的定义域与r的值有关，但是不管r取何值，该函数在{\displaystyle (0,+\infty )}(0,+\infty )上总有意义。
几种常见的幂函数图像

指数函数

称形如{\displaystyle f(x)=a^{x}}f(x)=a^{x}的函数为指数函数，其中a是常数，{\displaystyle a>0}a>0且{\displaystyle a\neq 1}a\neq 1。该函数的定义域为{\displaystyle (-\infty ,+\infty )}(-\infty,+\infty)，值域为{\displaystyle (0,+\infty )}(0,+\infty )
指数函数'"`UNIQ--postMath-0000000B-QINU`"'的图像

对数函数

称形如{\displaystyle y=\log _{a}x\!}y=\log _{a}x\!的函数为对数函数，其中{\displaystyle a>0}a>0且{\displaystyle a\neq 1}a\neq 1，是指数函数{\displaystyle y=a^{x}}y=a^x的反函数。该函数定义域为{\displaystyle (0,+\infty )}(0,+\infty )，值域为{\displaystyle (-\infty ,+\infty )}(-\infty,+\infty)
e, 绿色函数底数是2，而蓝色函数底数是1/2。在数轴上每个刻度是半个单位。所有底数的对数函数都通过点(1,0)，因为任何数的0次幂都是1，而底数 β 的函数通过点(β ,1)，因为任何数的1次幂都是自身1。曲线接近 y 轴但永不触及它，因为x=0的奇异性。

三角函数

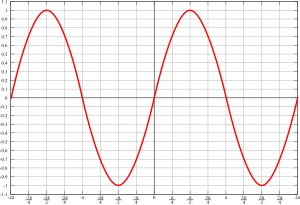
正弦函数

称形如{\displaystyle f(x)=\sin x}f(x)=\sin x的函数为正弦函数，它的定义域为{\displaystyle (-\infty ,+\infty )}(-\infty,+\infty)，值域为{\displaystyle [-1,1]}[-1,1]，最小正周期为{\displaystyle 2\pi }2\pi 。
正弦函数图像

余弦函数

称形如{\displaystyle f(x)=\cos x}f(x)=\cos x的函数为余弦函数，它的定义域为{\displaystyle (-\infty ,+\infty )}(-\infty,+\infty)，值域为{\displaystyle [-1,1]}[-1,1]，最小正周期为{\displaystyle 2\pi }2\pi 。
余弦函数图像

正切函数

称形如{\displaystyle f(x)=\tan x}f(x)=\tan x的函数为正切函数，它的定义域为{\displaystyle \{x|x\neq k\pi +{\frac {\pi }{2}},\,k\in \mathbb {Z} \}}\{x|x\neq k\pi +{\frac {\pi }{2}},\,k\in {\mathbb {Z}}\}，值域为{\displaystyle (-\infty ,+\infty )}(-\infty,+\infty)，最小正周期为{\displaystyle \pi }\pi 。

正切函数图像

余切函数

称形如{\displaystyle f(x)=\cot x}f(x)=\cot x的函数为余切函数，它的定义域为{\displaystyle \{x|x\neq k\pi ,\,k\in \mathbb {Z} \}}\{x|x\neq k\pi ,\,k\in {\mathbb {Z}}\}，值域为{\displaystyle (-\infty ,+\infty )}(-\infty,+\infty)，最小正周期为{\displaystyle \pi }\pi 。
余切函数]图像

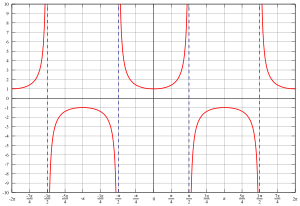
正割函数

称形如{\displaystyle f(x)=\sec x}f(x)=\sec x的函数为正割函数，它的定义域为{\displaystyle \{x|x\neq k\pi +{\frac {\pi }{2}},\,k\in \mathbb {Z} \}}{\displaystyle \{x|x\neq k\pi +{\frac {\pi }{2}},\,k\in \mathbb {Z} \}}，值域为{\displaystyle (-\infty ,-1]\cup [1,+\infty )}(-\infty ,-1]\cup [1,+\infty )，最小正周期为{\displaystyle 2\pi }2\pi 。
正割函数图像

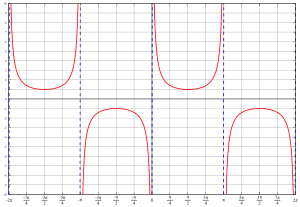
余割函数

称形如{\displaystyle f(x)=\csc x}f(x)=\csc x的函数为余割函数，它的定义域为{\displaystyle \{x|x\neq k\pi ,\,k\in \mathbb {Z} \}}\{x|x\neq k\pi ,\,k\in {\mathbb {Z}}\}，值域为{\displaystyle (-\infty ,-1]\cup [1,+\infty )}(-\infty ,-1]\cup [1,+\infty )，最小正周期为{\displaystyle 2\pi }2\pi 。
余割函数图像

反三角函数

其它常见初等函数

双曲函数

双曲正弦函数：{\displaystyle y=\sinh x={\frac {e^{x}-e^{-x}}{2}}}y=\sinh x={\frac {e^{x}-e^{{-x}}}{2}}
双曲余弦函数：{\displaystyle y=\cosh x={\frac {e^{x}+e^{-x}}{2}}}y=\cosh x={\frac {e^{x}+e^{{-x}}}{2}}
双曲正切函数：{\displaystyle y=\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}}y=\tanh x={\frac {\sinh x}{\cosh x}}={\frac {e^{x}-e^{{-x}}}{e^{x}+e^{{-x}}}}

反双曲函数

反双曲正弦函数：{\displaystyle y=\operatorname {arsinh} \,x=\ln(x+{\sqrt {x^{2}+1}})}y=\operatorname {arsinh}\,x=\ln(x+{\sqrt {x^{2}+1}})
反双曲正切函数：{\displaystyle y=\operatorname {arcosh} \,x=\ln(x+{\sqrt {x^{2}-1}})}y=\operatorname {arcosh}\,x=\ln(x+{\sqrt {x^{2}-1}})

posted @ 2019-03-28 09:13  扫地猿  阅读(3162)  评论(0)  编辑  收藏  举报