2019杭电多校第7场总结
差一点就爆零了,杭电多校也是从来没有让人失望😂。最后5分钟a了K题,摆脱爆零。
开始的时候一直在看a题,一波思考后成功t了一发,又没啥解决方案,于是和队友去看F,在一番思维碰撞后,我们写出了自认为完美无缺~~(事实上题意都理解错了喂!!!)~~ 的代码,wa了好几发。赛后看题解,完全理解错了。。。。。。至于K题,本来开始不久时,队友说是到期望的题,由于对期望知识并不了解,一开始没有选择去碰它,就只是帮队友算了一下样例是怎么来的。最后一个小时,看K题过的人还算多,于是打算尝试一下。
k题题意大概就是你想升级,升级所需的钱为ai,升级成功的概率为ri/si,如果失败则降为xi级。多个询问,问从l级升到r级的所需钱的期望是多少。
失败就会退到xi级,假设我们是一级一级往后推,那么升到上一级的期望我们是知道的,所以我们就可以列出递推公式。设失败后,我们要升到原来级数所需钱的期望为d。于是有升到下一级的钱的期望D的公式。
高中的时候就学过如何算这种式子,等差乘等比,公比为(1-r/s),公差为(a+d),直接错位相减法,求极限。
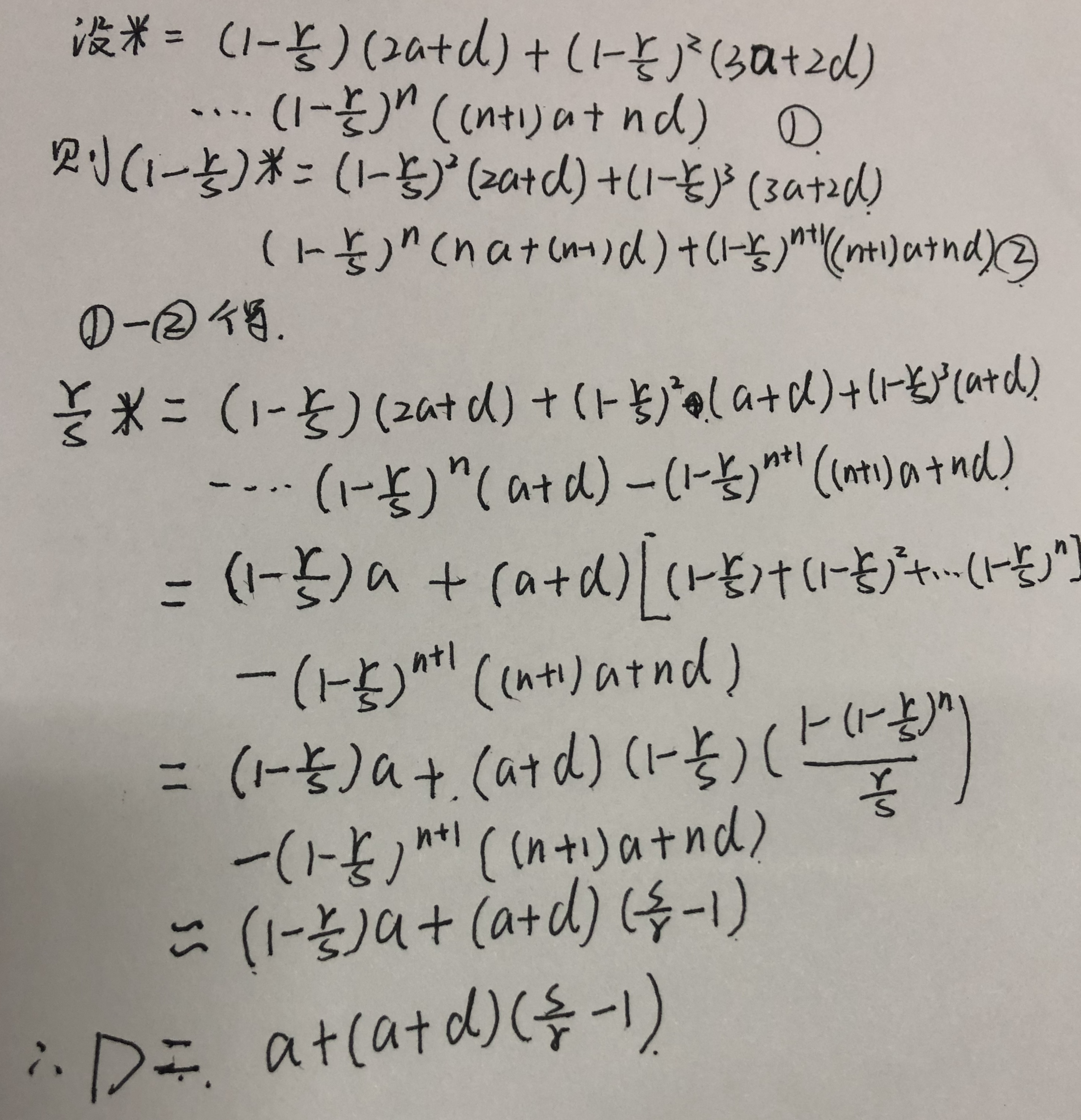得出D=a+(a+d)*(s/r-1)。那么问题就迎刃而解了。
因为是l到r的查询,我们可以设一个数组Sum前缀求从1升到i的钱的期望。答案就是右边减左边啦。
值得注意的是由于有取模,还有除法,得用逆元,还有相减取模的时候一定要注意加上MOD再取模😂,我就是因为这样wa了。。。。。。。。。代码呈上
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
const int MAXN=5e5+10;
const double eps=1e-8;
const int MOD=1000000007;
using namespace std;
typedef long long ll;
ll d[500005],r,s,x,a,Sum[500005];
ll qpmod(ll a,ll n)
{
ll ret=1;
while(n)
{
if(n&1)
ret=(ret*a)%MOD;
a=(a*a)%MOD;
n>>=1;
}
return ret;
}
ll inv(ll a)
{
return qpmod(a,MOD-2)%MOD;
}
int main()
{
int t;
scanf("%d",&t);
while(t--)
{
ll n,q;
scanf("%lld%lld",&n,&q);
d[0]=0,Sum[0]=0;
memset(Sum,0,sizeof(Sum));
memset(d,0,sizeof(d));
for(int i=1;i<=n;i++)
{
scanf("%lld%lld%lld%lld",&r,&s,&x,&a);
ll sum=(Sum[i-1]+MOD-Sum[x-1]+a)%MOD;
d[i]=(a+sum*(s*inv(r)%MOD+MOD-1)%MOD)%MOD;
Sum[i]=(Sum[i-1]+d[i])%MOD;
}
ll L,R;
for(int i=0;i<q;i++)
{
scanf("%lld%lld",&L,&R);
printf("%lld\n",(Sum[R-1]+MOD-Sum[L-1])%MOD);
}
}
return 0;
}
其他补了再说吧。。。。。。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号