最优化概述

　　最优化概述分为：最优化定位、最优化工具、最优化问题、最优化方法、求解的过程。

1.1最优化定位

1.1.1最优化课程定位

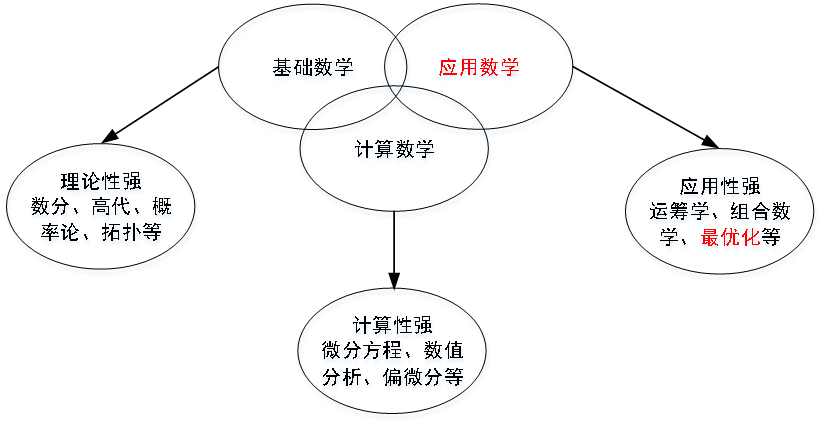
　　最优化是应用数学的一个分支，同时也是学习运筹学、机械工程设计、控制论等课程的基础，更多的体现在实际应用问题的建模与求解中。

   　　　　　　　　　

应用：无人机路径规划、机械臂设计、智能物流调度。　　　　　　　　　　　　　　

1.1.2最优化研究内容

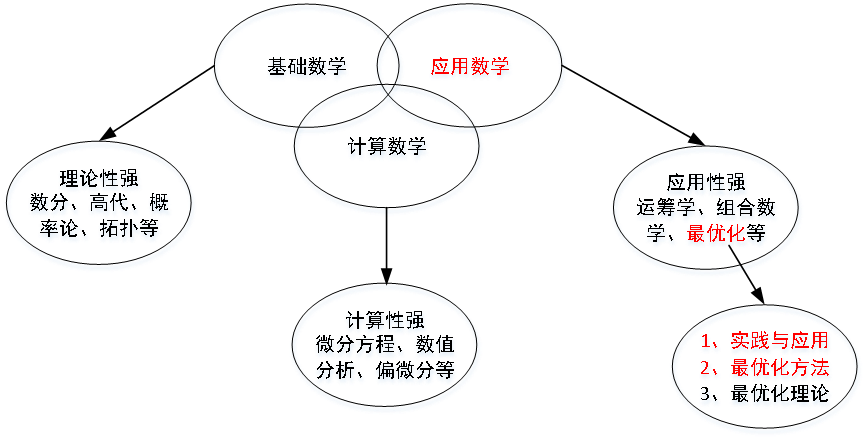
　　最优化学科的研究主要包括三个方面：实践与应用（如何对实际问题建模与求解）、最优化方法（如何设计高效的求解方法）、最优化理论（如何理论上证明方法的可行性）。

 

 

1.1.3最优化数学基础

最优化涉及的数学知识：矩阵、多项式、向量、求导、矩阵和向量范数等。

　　　　向量范数　　　　　　　　　　　　　　矩阵范数

 

 

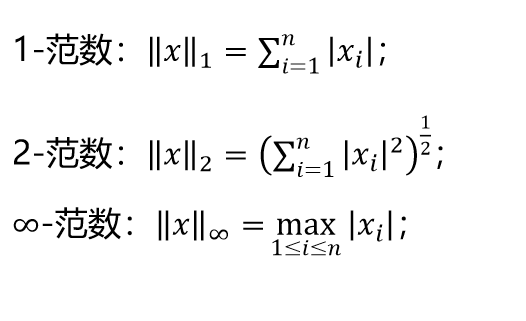
 　　　　　　　　　　一阶导数或梯度

 

 

 

 

 

 

 

 

 

 

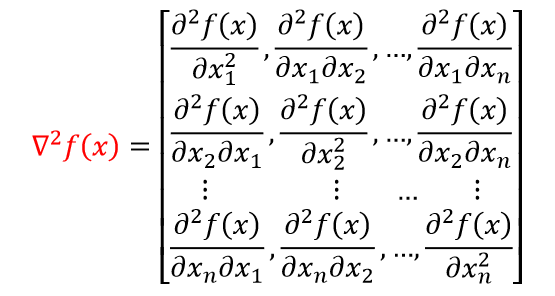
1.2最优化工具

　　常用编程软件：MATLAB，C++，Python，Julia，其他编程语言也可，彼此相通。

　　目前，推荐主修MATLAB，自己用起来顺手的编程语言最重要。

　　1.实验仿真用的较多，特别是应用问题的数学建模；

　　2.简单、功能多、自带有优化方法工具箱，易于做论文；

　　3.已有资源代码多数为MATLAB实现；

 

1.3最优化问题

 

 

 

 1.3.1最优化问题定义

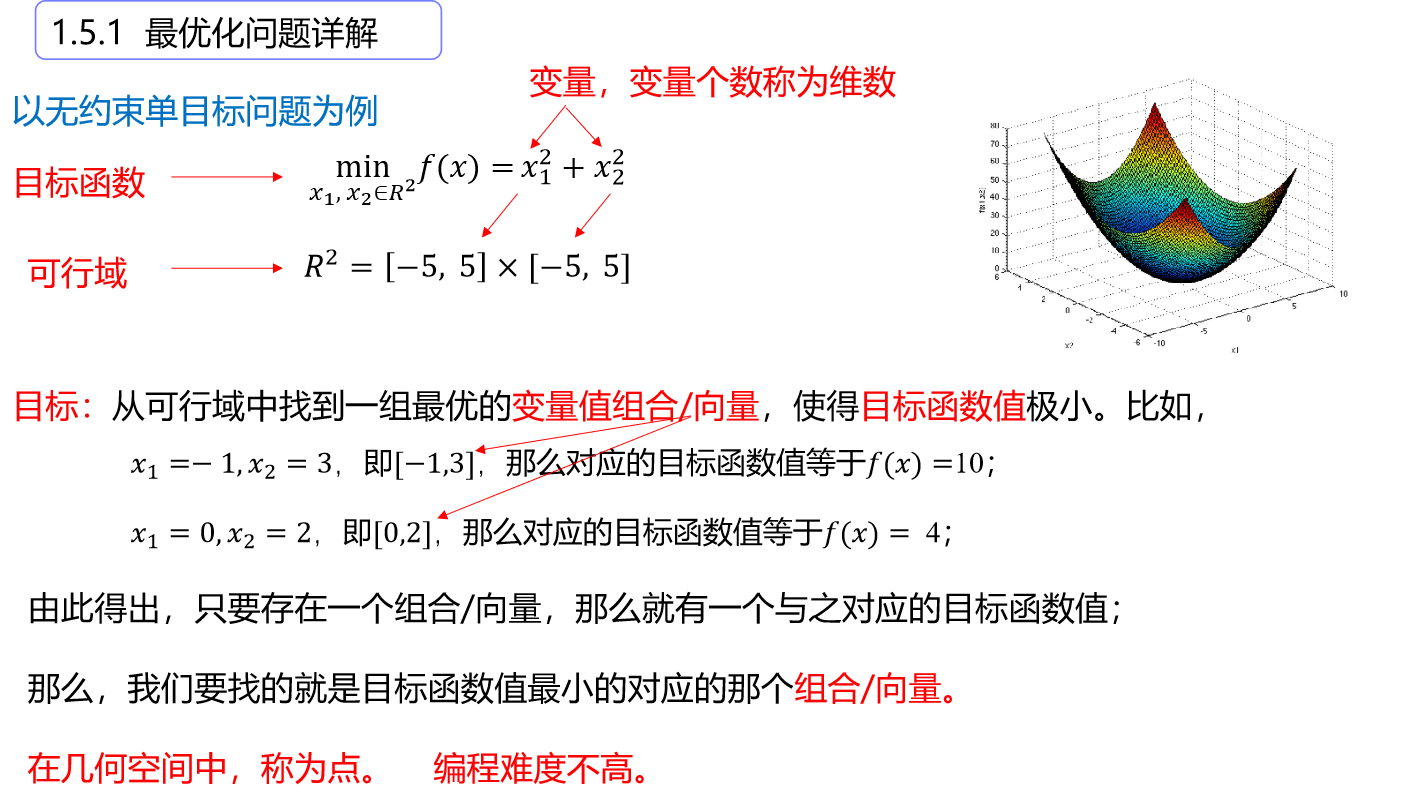
 　　通过对实际问题的分析和信息提取，建立起一种数学模型，该模型包括极小min或极大max化某一个或多个目标，以及若干限制条件。

 

 

 

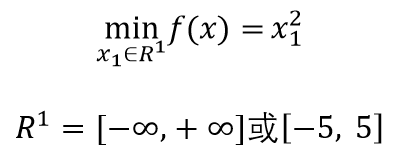
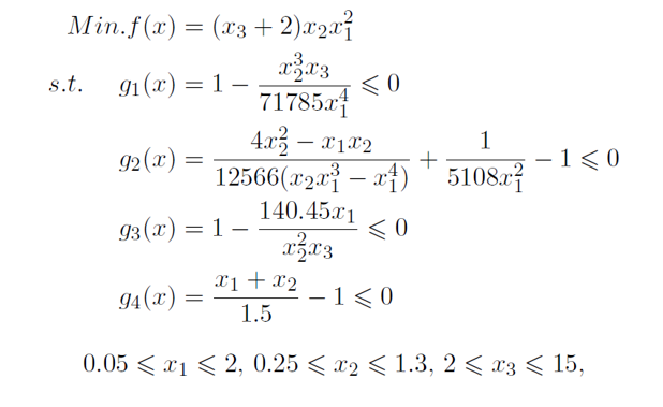
 1.3.2最优化问题分类

　　根据待优化目标的个数，最优化目标可分为：无约束单目标优化问题、约束单目标优化问题、动态多目标优化问题。

 　　　　　　

1.3.3最优化问题模型

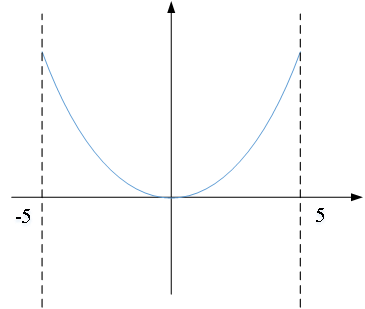
　　单目标优化问题：

　　　　　　

 

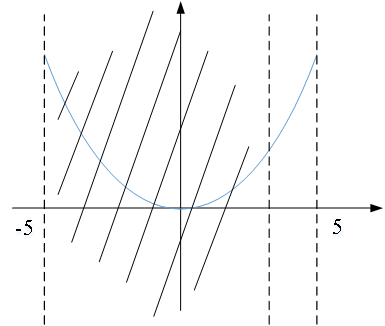
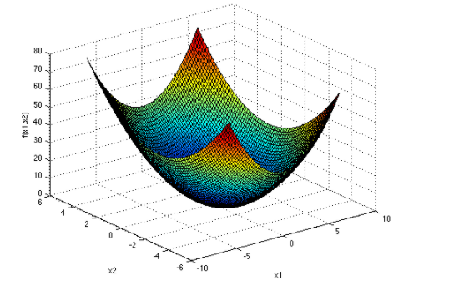
无约束单目标优化问题：即不存在约束条件。

 

 

 

 

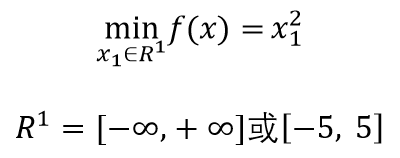
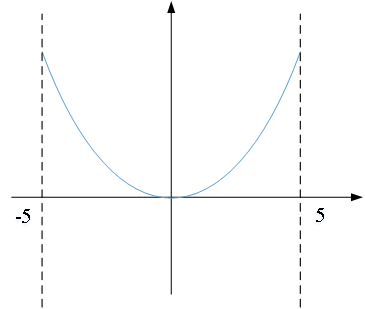
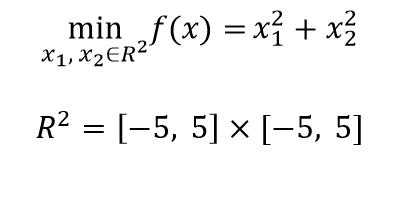
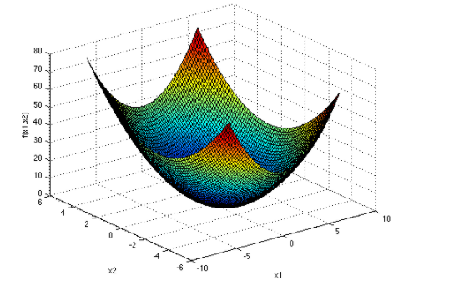
 （ps3：其中x1、x2的定义域分别为[-5,5]、[-5,5]）

 

约束单目标优化问题，即，存在约束条件，等式约束和不等式约束。

 

 

 

 

 

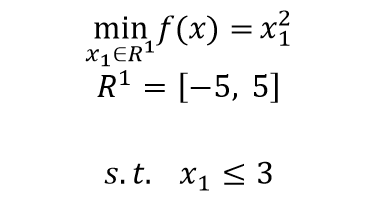
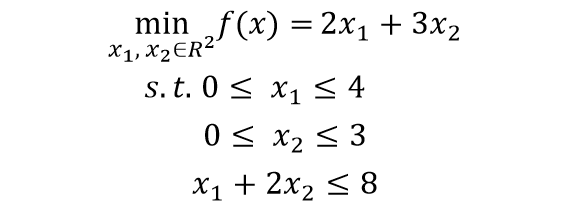
 最优化问题模型考虑：

 

 

 

 

 

 

 　　　　　　　　　　　　

 

 

 

 

 

 

 

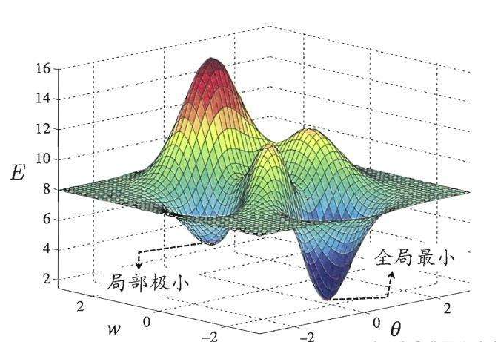
 多目标优化问题：

 

 

 

 

 1.4最优化方法

1.4.1最优化方法定义

 

 

 

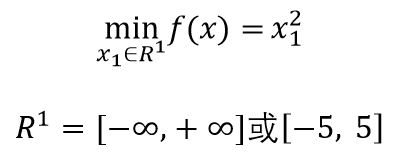
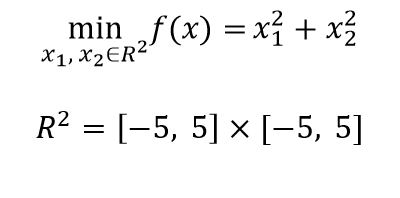
1.4.2最优化方法分类

经典优化方法：

 

 　　以导数为特征的一类迭代优化方法，比如最速下降法、牛顿法、共轭梯度法等。

　　优点：计算精度高。缺点：需要目标函数可导，限制较大。

　　（不做进一步研究。）

智能优化方法：

　　以群体相互协作、随机搜索为特征的一类迭代方法。

　　优点：速度快、灵活性较强不受导数的影响。缺点：非精确搜索，精度可能不高。

　　（重点研究。）

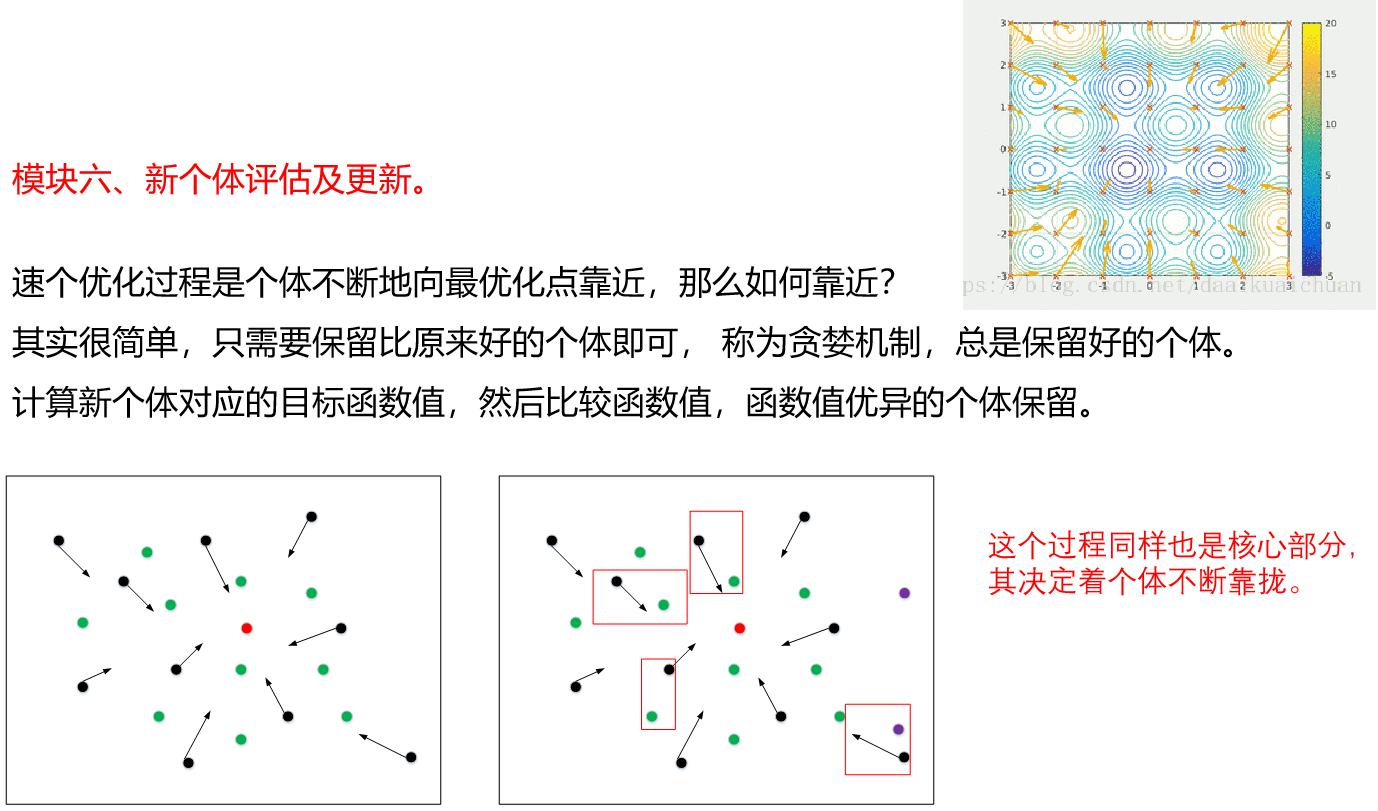
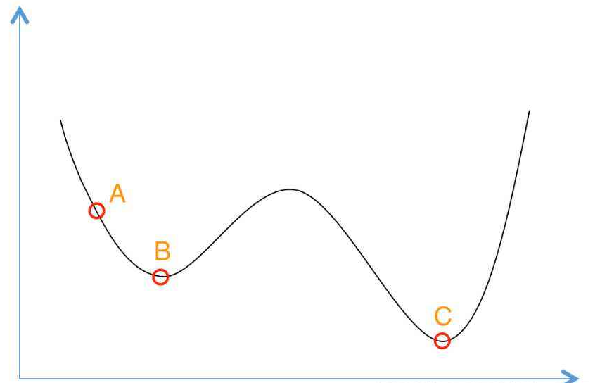
迭代机制思想：以最小化为例，通过不断的拉近得到计算得到点和最优解之间的距离，越近越好。即，每一次循环/迭代计算得到的点都比上一代得到的点要小，以此进一步逼近/靠近最优解。

目标：在每一次循环/迭代完，找到当前循环/迭代的最小值。

 

考虑：

 

 迭代法基本思想：给定一个初始点(x^t,t=0)，按照某一迭代规则产生一个迭代序列{x^t}（函数值降序，最小化），若该序列是有限的，则最后一个点就是问题的最优解。

收敛曲线图：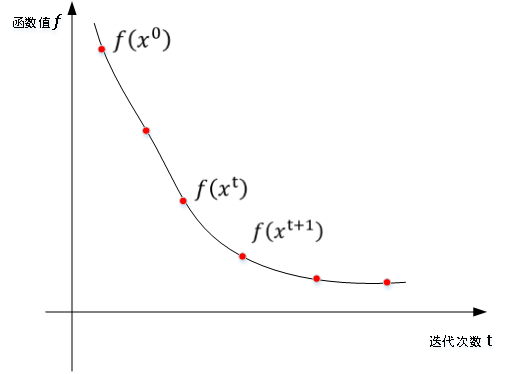

通常通过设置算法终止条件（最小误差或最大迭代次数等），让迭代序列有限。

 1.4.3智能优化方法

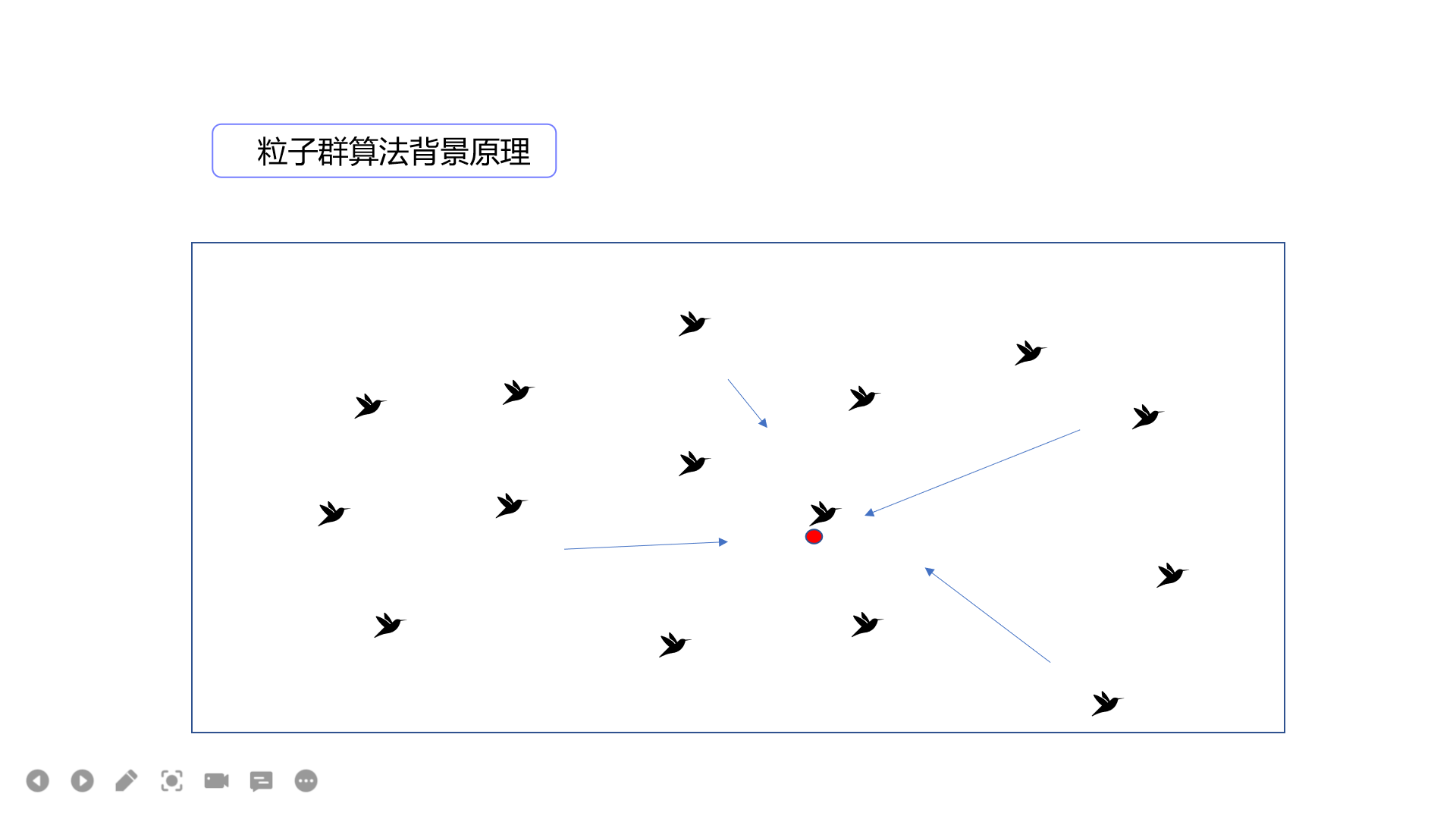
现存智能优化方法有很多， 流行的：比如进化算法(EA)、粒子群算法(PSO)、蚁群算法(ACO)、差分进化算法(DE)等； 最新的：比如布谷鸟算法(CS)、狼群算法(GWO)、鲸鱼算法（GOA）等；

 

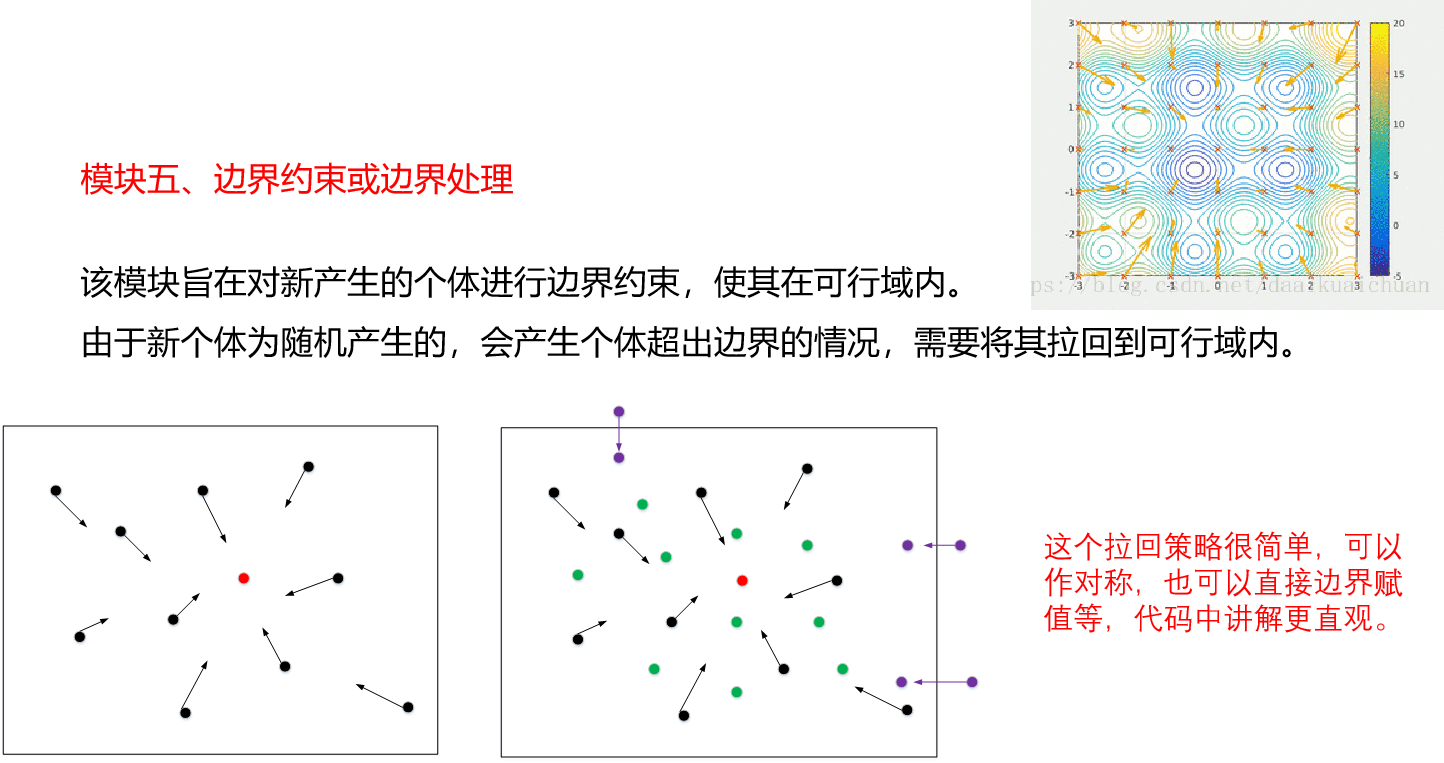
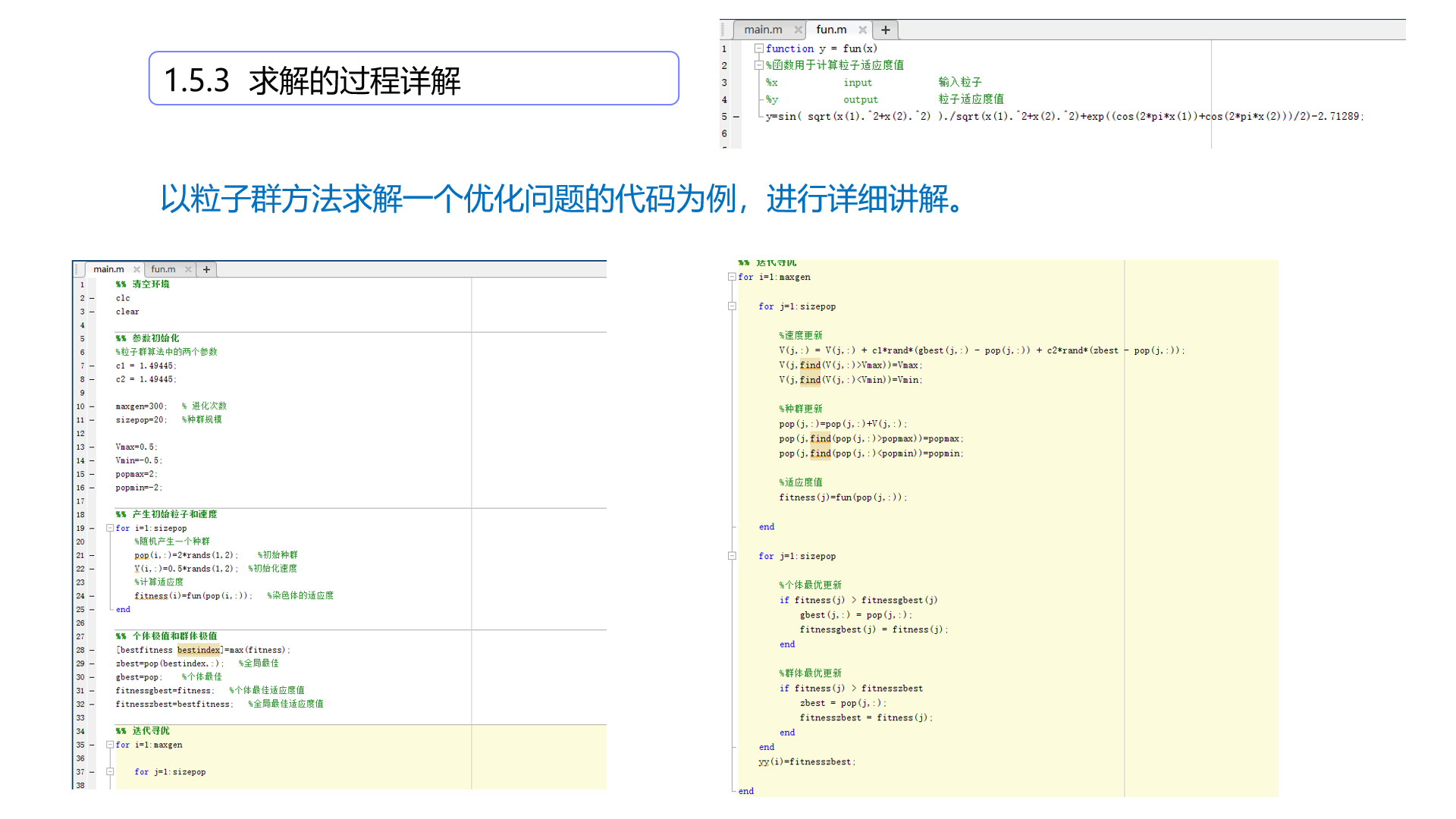
1.5求解的过程

 

 

 

 

1.5.2最优化方法详解

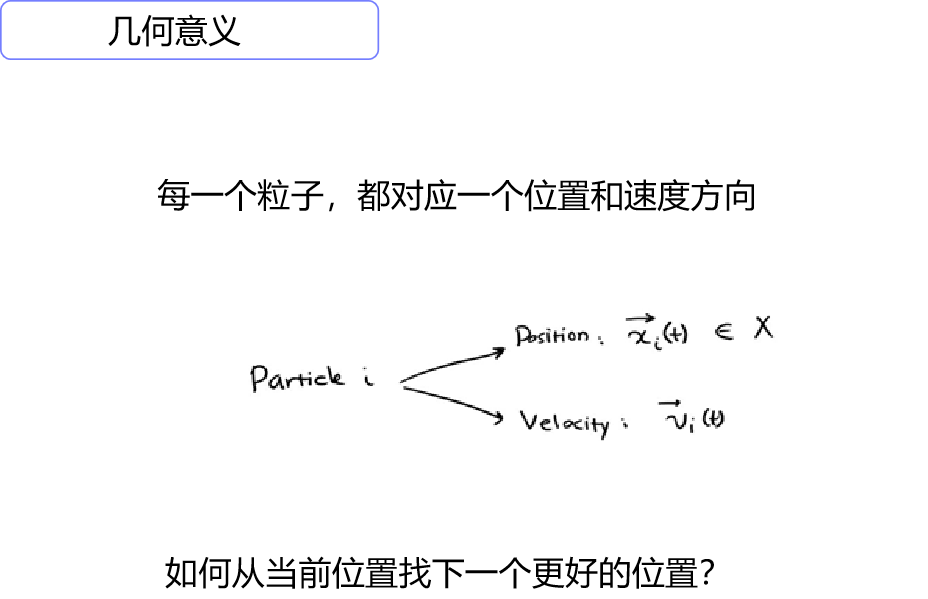
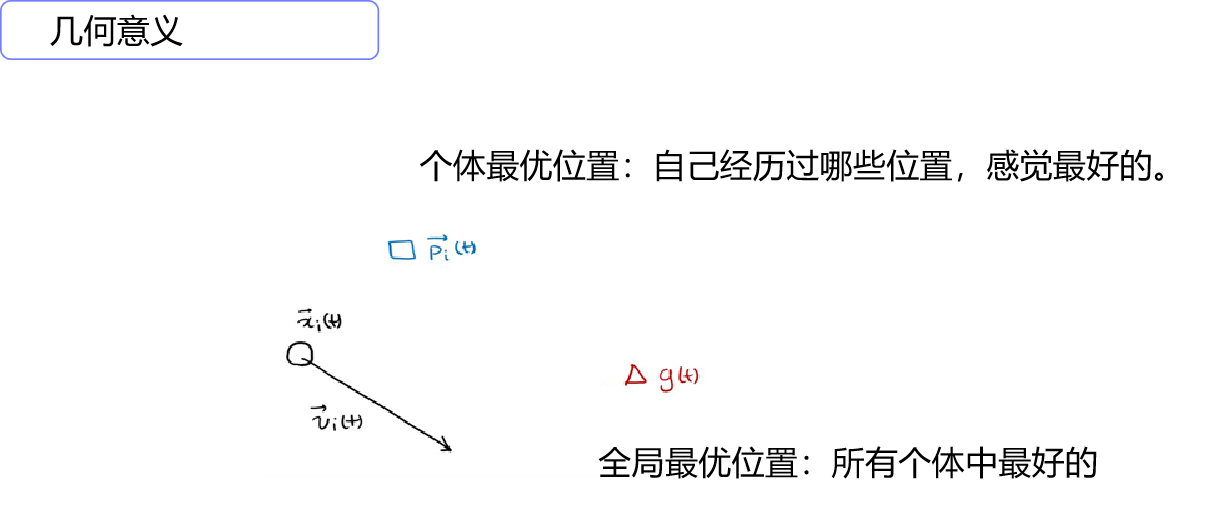
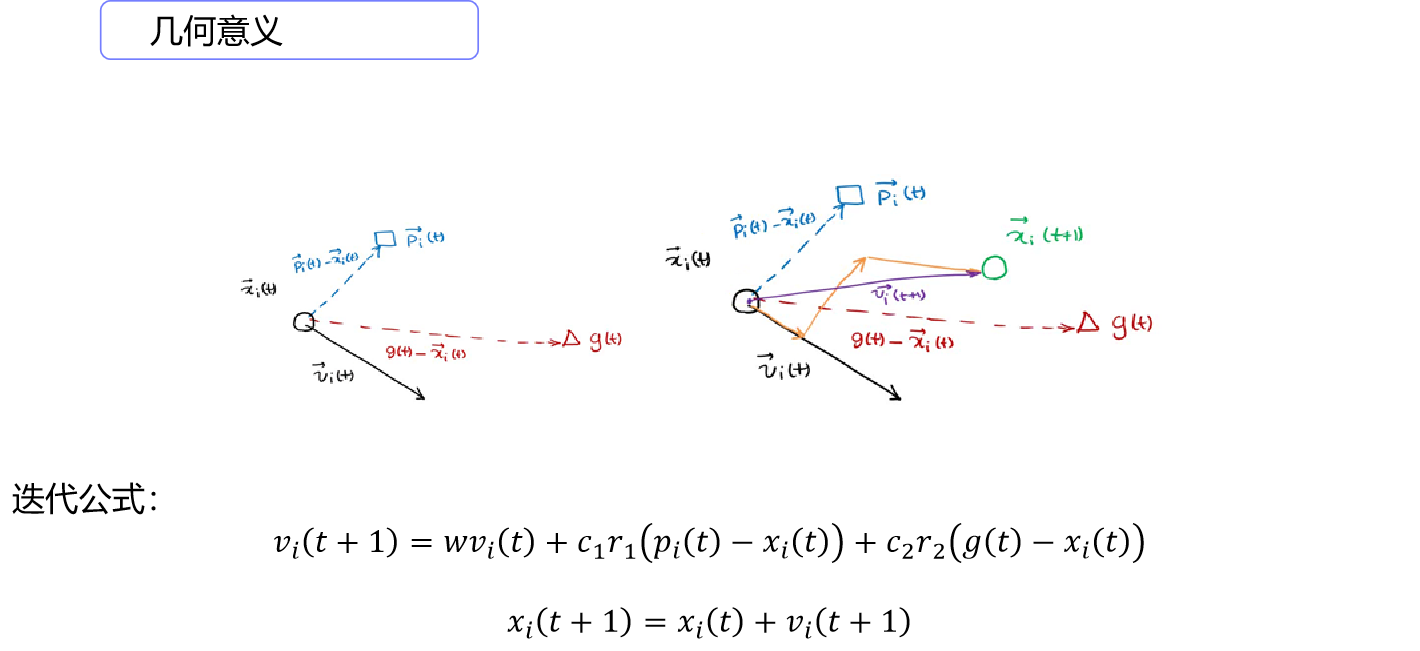
以智能优化方法为例，群体搜索为特征

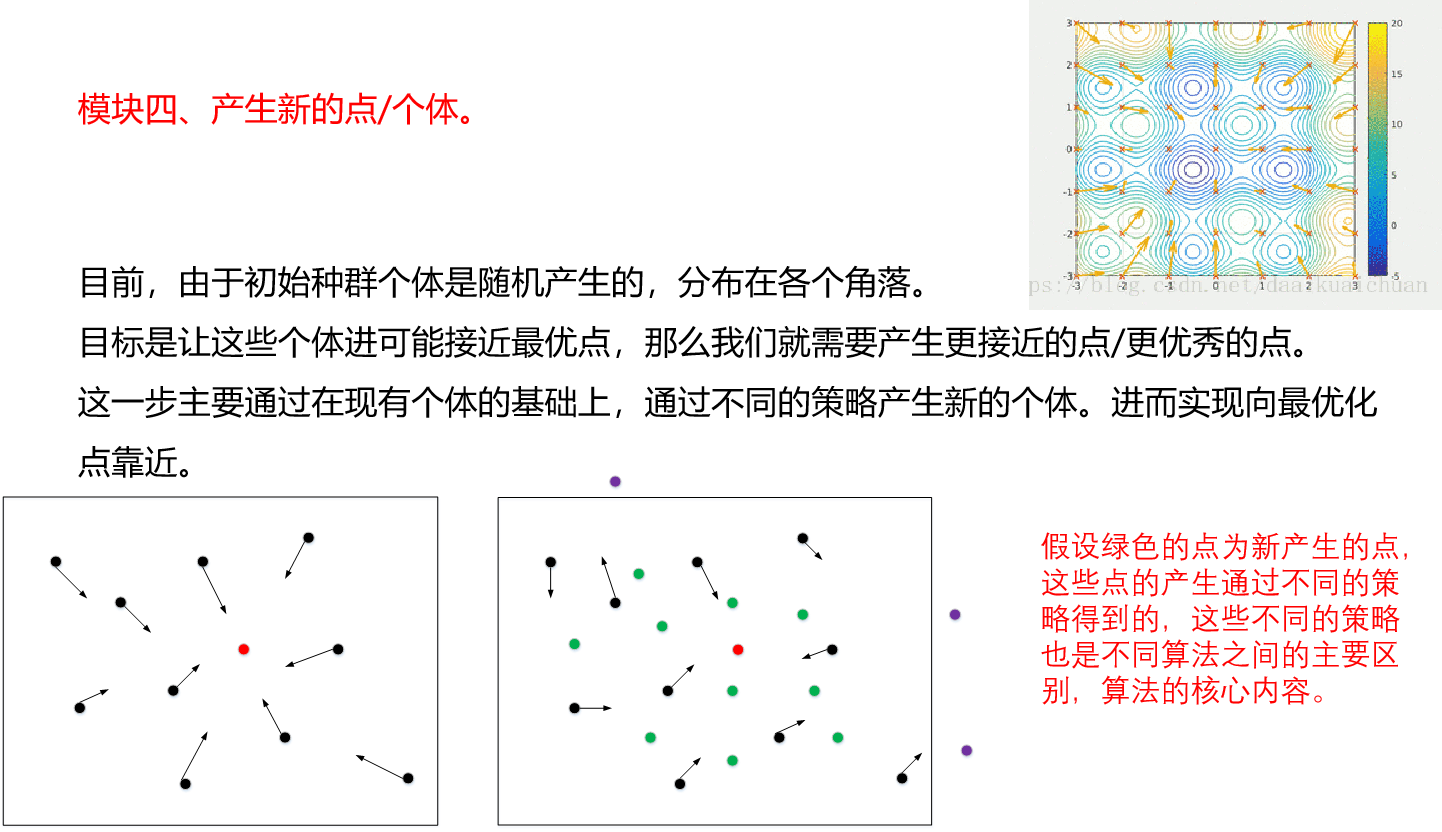
模块一、相关参数设置

参数设置包括：算法的相关控制参数，优化问题的相关参数，停止准则等