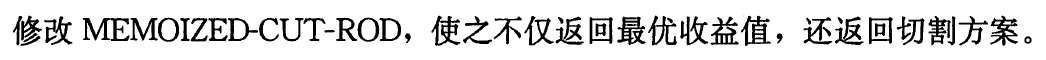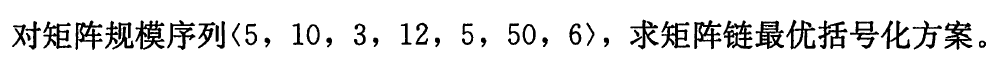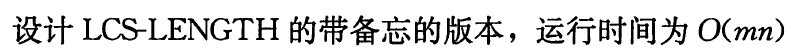test
# Colab 相关设置项
# Mount Google Drive
from google.colab import drive # import drive from google colab
ROOT = "/content/drive" # default location for the drive
drive.mount(ROOT) # we mount the google drive at /content/drive
# change to clrs directionary
%cd "/content/drive/My Drive/Colab Notebooks/CLRS/CLRS_notes"
Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).
/content/drive/My Drive/Colab Notebooks/CLRS/CLRS_notes
%mkdir ch15
mkdir: cannot create directory ‘ch15’: File exists
import imp
import random
15.0 序论
- 动态规划与分治方法类似,都是通过组合子问题的解来求解原问题
- 但动态规划适用于子问题重叠的情况,即不同的子问题具有公共的子子问题
- 动态规划通常用来求解最优化问题
- 通常求解的是问题的一个最优解,而不是最优解,因为最优解可能有多个
- 通常按以下 4 个步骤来设计动态规划算法
- 刻划一个最优解的结构特征
- 递归的定义最优解的值
- 计算最优解的值,通常采用自底向上的方法
- 利用计算的信息构造出最优解
15.1 钢条切割问题
- 问题描述
- 给定一条长度为 \(n\) 的钢管和一个价格表 \(p_i(i = 1, 2, \cdots)\),求使销售收益 \(r_n\) 最大的钢条切割方案
- 如果长度为 \(n\) 英寸的钢条的价格 \(p_n\) 足够大,最优解可能是完全不需要切割
- 给定一条长度为 \(n\) 的钢管和一个价格表 \(p_i(i = 1, 2, \cdots)\),求使销售收益 \(r_n\) 最大的钢条切割方案
最优子结构
- 对于 \(r_n(n \ge 1)\),可以用更短的钢条的最优切割收益来描述:
-
\[r_n = max(p_n, r_1+r_{n-1}, r_2+r_{n-2}, \cdots, r_{n-1} + r_{1}) \]
- \(p_n\) 对应不切割
- 其它方案对应先将钢条切割成 \(i\) 和 \(n-i\) 两段,接着求解这两段的最优切割收益 \(r_i\) 和 \(r_{n-i}\)
-
- 钢条切割问题满足最优子结构的性质
- 问题的最优解由相关子问题的最优解组合而成,而这些子问题可以独立求解
- 简化子问题
- 可以先将钢条从左边切下长度为 \(i\) 的一段,然后只对右边剩下的长度为 \(n-i\) 的钢条进行切割
-
\[r_n = \max\limits_{1\le i \le n}(p_i + r_{n-i}) \]
- 简化后,原问题的最优解只包含一个相关子问题的解,而不是两个
自底向下的递归实现
代码实现
%%writefile ch15/cut_rod.py
"""钢条切割问题"""
def cut_rod(p, n):
if n == 0:
return 0
q = float('-inf')
for i in range(1, n+1):
q = max(q, p[i-1] + cut_rod(p, n-i))
return q
Overwriting ch15/cut_rod.py
import ch15.cut_rod
from ch15.cut_rod import cut_rod
p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
cut_rod(p, 4)
10
复杂度分析
- \(n=4\) 时的调用过程
-
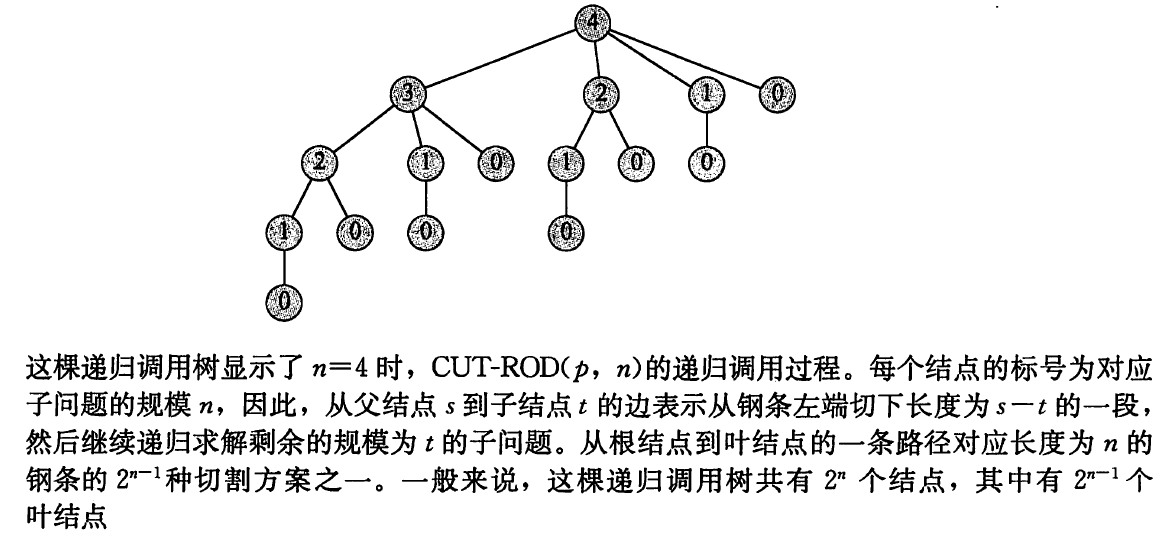
- 长度为 \(n\) 的钢条切割共有 \(2^{n-1}\) 个节点,对应 \(2^{n-1}\) 种切割方案
- 对于 \(1, 2, \cdots, n-1\) 处的切割点,可以选择切割或者不切割
-
- 总的调用次数
-
\[T(n) = 1 + \sum^{j=0}_{n-1}T(j) = 2^n \]
-
使用动态规划方法求解最优钢条切割问题
- 朴素的递归算法效率极低,因为其会反复求解相同的子问题。而动态规划方法会仔细安排求解顺序,对每个子问题只求解一次
- 子问题的求解结果会被保存起来,下次再需要时,直接查询即可
- 动态规划付出额外的内存空间来节省计算时间,是典型的时空权衡(time-memory trade-off)的例子
- 动态规划在时间上的节省可能是非常巨大的
- 可以将一个指数时间的解转化为一个多项式时间的解
- 动态规划有两种等效的实现方法
- 带备忘录的自顶向下法(top-down with memoization)
- 仍按递归的形式编写过程,但过程会保存每个子问题的解,当需要子问题的解时,过程会首先检查是否保存了此解。
- 自底向上法(bottom-up method)
- 此方法需要恰当的定义子问题“规模”,使得任何子问题都只能依赖“更小的”子问题的求解
- 可以将子问题按规模排序,按由小至大的顺序进行求解
- 两种方法有相同的渐近运行时间,但在特殊情况下有差异
- 自顶向下算法可能不用计算所有可能的子问题
- 由于没有递归函数调用的开销,自底向上方法的时间复杂性函数通常具有更小的系数
带备忘录的自顶向下法的代码实现
%%writefile -a ch15/cut_rod.py
def memoized_cut_rod(p, n):
"""带备忘发的自顶向下法"""
r = [float('-inf')] * (n+1)
return memoized_cut_rod_aux(p, n, r)
def memoized_cut_rod_aux(p, n, r):
""""带备忘录的自顶向下法的辅助函数"""
if r[n] >=0:
return r[n]
if n == 0:
q = 0
else:
q = float('-inf')
for i in range(1, n+1):
q = max(q, p[i-1] + memoized_cut_rod_aux(p, n-i, r))
r[n] = q
return q
Appending to ch15/cut_rod.py
imp.reload(ch15.cut_rod)
from ch15.cut_rod import memoized_cut_rod
p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
memoized_cut_rod(p, 4)
10
自底向上法的代码实现
%%writefile -a ch15/cut_rod.py
def bottom_up_cut_rod(p, n):
"""自底向上法"""
r = [float('-inf')] * (n + 1)
r[0] = 0
for i in range(1, n+1):
q = float('-inf')
for j in range(1, i+1):
q = max(q, p[j-1] + r[i-j])
r[i] = q
return r[-1]
Appending to ch15/cut_rod.py
imp.reload(ch15.cut_rod)
from ch15.cut_rod import bottom_up_cut_rod
p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
bottom_up_cut_rod(p, 4)
10
复杂度分析
- 自底向上算法和自顶向下算法具有相同的渐近运行时间,均为 \(\Theta(n^2)\)
子问题图
- 思考动态规划问题时,应该弄清楚所涉及的子问题及子问题之间的依赖关系,可以借助子问题图来实现
- 子问题图
- 是一个有向图,每个顶点唯一地对应一个子问题
- 若求子问题\(x\)的最优解时需要直接用到子问题\(y\)的最优解,那么在子问题图中就会有一条从子问题\(x\)的顶点到子问题\(y\)的顶点的有向边
- 可以将子问题图看做自顶向下递归调用树的“简化版”或“收缩版”
- 因为树中所有对应相同子问题的结点合并为图中的单一顶点,相关的所有边都从父结点指向子结点
- 可以将子问题图看做自顶向下递归调用树的“简化版”或“收缩版”
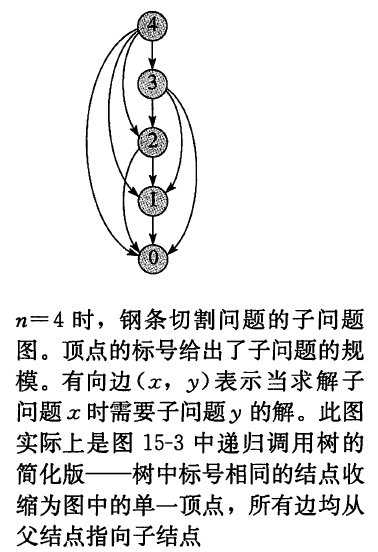
- 钢条切割问题的子问题图
-
- 子问题图 \(G=(V, E)\) 的规模可以用来确定动态规划算法的运行时间
- 每个子问题只求解一次,一个子问题的求解时间与子问题中对应顶点的度(出射边的数目) 成正比
- 子问题的数目等于子问题中的顶点数
- 因此,动态规划算法的运行时间与项点和边的数量呈线性关系
重构解
- 可以扩展钢条切割的动态规划算法,使得对每个子问题,不仅保存最优收益值,还保存相应的切割方案
代码实现
%%writefile -a ch15/cut_rod.py
def extend_bottom_up_cut_rod(p, n):
"""保存最优切割方案"""
r = [float('-inf')] * (n+1) # 存放最优收益
s = [0] * n # 保留最佳切割方案
r[0] = 0
for i in range(1, n+1):
for j in range(1, i+1):
if r[i] < p[j-1] + r[i-j]:
r[i] = p[j-1] + r[i-j]
s[i-1] = j
return r, s
def print_cut_rod(s, n=None):
"""打印出最佳切割方案"""
n = len(s) - 1 if n == None else n
while n >= 0:
print(s[n], end=" ")
n = n - s[n]
Appending to ch15/cut_rod.py
import ch15.cut_rod
imp.reload(ch15.cut_rod)
from ch15.cut_rod import print_cut_rod, extend_bottom_up_cut_rod
p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
_, s = extend_bottom_up_cut_rod(p, 7)
print_cut_rod(s)
1 6
练习
15.1-1
-
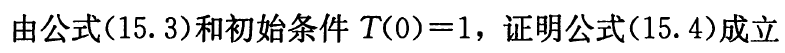
-
可采用数学归纳法证明
- 假设 \(x< n - 1\) 时, \(T(x) = 2^x\)
- 则当 \(x=n\) 时,有
-
\[T(n) = 1 + \sum_{j=0}^{n-1} T(j) = 1 + 1 + 2^1 + 2^2 + \cdots + 2^{n-1}= \]
-
- 证毕
15.1-2
-

-
当 \(n=4\) 时,如果采用贪心法,方案为 3 + 1, 收益为 9。而最优方案为 2 + 2, 收益为 10
15.1-3
-

-
切割成本为 \(c\), 相当于需要添加选择成本
%%writefile -a ch15/cut_rod.py
def cut_rod_with_cost(p, n, c):
"""练习题 15.1-3,需要考虑切割成本"""
r = [float('-inf')] * (n+1)
s = [0] * n
r[0] = c # 避免后续判断是否需要加上切割成本
for i in range(1, n+1):
for j in range(1, i+1):
t = p[j-1] + r[i-j] - c
if t > r[i]:
r[i] = t
s[i-1] = j
return r, s
Appending to ch15/cut_rod.py
import ch15.cut_rod
imp.reload(ch15.cut_rod)
from ch15.cut_rod import cut_rod_with_cost, print_cut_rod
p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
r, s = cut_rod_with_cost(p, 10, 1)
r[1:]
[1, 5, 8, 9, 12, 17, 17, 21, 24, 30]
s
[1, 2, 3, 2, 2, 6, 1, 2, 3, 10]
15.1-4
%%writefile -a ch15/cut_rod.py
def extend_memoized_cut_rod(p, n):
"""返回切割方案的带备忘发的自顶向下法"""
r = [float('-inf')] * (n+1)
s = [0] * n
extend_memoized_cut_rod_aux(p, n, r, s)
return r, s
def extend_memoized_cut_rod_aux(p, n, r, s):
""""返回切割方案的带备忘录的自顶向下法的辅助函数"""
if r[n] >=0:
return r[n]
if n == 0:
q = 0
else:
q = float('-inf')
for i in range(1, n+1):
t = p[i-1] + extend_memoized_cut_rod_aux(p, n-i, r, s)
if t > q:
q = t
s[n-1] = i
r[n] = q
return q
Appending to ch15/cut_rod.py
import ch15.cut_rod
imp.reload(ch15.cut_rod)
from ch15.cut_rod import extend_memoized_cut_rod, print_cut_rod
p = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
r, s = extend_memoized_cut_rod(p, 7)
print("最优收益为: ", r[-1])
print("最优切割方案为")
print_cut_rod(s)
最优收益为: 18
最优切割方案为
1 6
15.1-5
-

-
使用一张表储存前 \(n-1\) 个计算的斐波那契数即可
%%writefile ch15/fibonacci.py
def fibonacci(n):
"""使用动态规划法计算斐波那契数列"""
if n == 0: return 0
if n == 1: return 1
r = [0] * (n+1)
r[0], r[1] = 0, 1
for i in range(2, n+1):
r[i] = r[i-1] + r[i-2]
return r[-1]
Overwriting ch15/fibonacci.py
from ch15.fibonacci import fibonacci
for i in range(11):
print(fibonacci(i), end=" ")
0 1 1 2 3 5 8 13 21 34 55
- 子问题图有 \(2n - 2\) 条边
- 因为从 \(2\) 至 \(n\), 每条边的度都为 2
- 有 \(n+1\) 个顶点
- 由边数和顶点数,可推得运行时间为 \(O(n)\)
15.2 矩阵链乘法
- 完全括号化的矩阵乘积链
- 此矩阵乘积链要么是单一的矩阵,要么是两个完全括号化的矩阵乘积链的积
- 如果矩阵链为 \(<A_1, A_2, A_3, A_4>\), 则共有 5 种完全括号化的矩阵乘积链
-
\[\begin{align} \]
-
&\left(A_{1}\left(\left(A_{2} A_{3}\right) A_{4}\right)\right)\
&\left(\left(A_{1} A_{2}\right)\left(A_{3} A_{4}\right)\right)\
&\left(\left(A_{1}\left(A_{2} A_{3}\right)\right) A_{4}\right)\
&\left(\left(\left(A_{1} A_{2}\right) A_{3}\right) A_{4}\right)
\end{align}$$
-
矩阵乘法所需的乘法次数
- 两个矩阵 \(A, B\) 只有相容,才能相乘
- \(A, B\) 相容是指 \(A\) 的列数等于 \(B\) 的行数
- 设 \(A\) 为 \(p \times q\) 的矩阵, \(B\) 是 \(q \times r\) 的矩阵,则 \(AB\) 需要的标量乘法次数为 \(pqr\)
- 两个矩阵 \(A, B\) 只有相容,才能相乘
-
矩阵链乘法问题
- 给定 \(n\) 个矩阵的链 \(<A_1, A_2, \cdots, A_n>\),矩阵 \(A_i\) 的规模为 \(p_{i-1}\times p_{i} (1 \le i \le n)\),求完全括号化方案,使得计算乘积 \(A_1A_2\cdots A_n\) 所需要标量乘法次数最少
计算括号化方案的数量
- 对 \(n\) 个矩阵的链,设 \(P(n)\) 表示可供选择的括号化方案数量
- \(n\ge 2\) 时,完全括号化的矩阵乘积可以描述成两个完全括号化的部分积相乘的形式,设划分点在第 \(k\) 个矩阵和第 \(k+1\) 个矩阵之间,其中 \(k= 1, 2, \cdots, n-1\) 中的任意一个值,可得如下递推公式
-
\[P(n)=\left\{\begin{array}{ll} \]
-
\sum_{k=1}^{n-1} P(k) P(n-k) & if\ n \ge 2
\end{array}\right.$$
- 由思考题 12.4 可知,得到的结果为卡塔兰数,括号化方案数与 \(n\) 呈指数关系,暴力求解时间代价大
应用动态规划方法
1. 最优化括号方案的结构特征
-
动态规划的第一步是寻找最优子结构
-
对于矩阵链乘法问题,最优子结构如下:
- 假设 \(A_iA_{i+1}\cdots A_{j}\) 的最优括号化方案的分割点在 \(A_k\) 和 \(A_{k+1}\) 之间。那么对 \(A_iA_{i+1}\cdots A_k\) 和 \(A_{k+1}A_{k+2}\cdots A_j\)进行括号化,可以直接采用独立求解它们时所得的最优化方案
-
利用最优子结构性质从子问题的最优解构造原问题的最优解
- 一个非平凡的矩阵链乘法问题实例的任何解都需要划分链,而任何最优解都是由子问题实例的最优解构成的
- 因此,可按下述步骤构造最优解
- 将问题划分为两个子问题(\(A_iA_{i+1}\cdots A_k\) 和 \(A_{k+1}A_{k+2}\cdots A_j\)的最优括号化问题
- 求出子问题实例的最优解,然后将子问题的最优解组合起来
- 必须保证在确定分割点时,已经考察了所有可能的划分点,这样就可以保证不会遗漏最优解。
2. 一个递归的求解方法
- 用 \(A_{i..j}\) 表示 \(A_iA_{i+1}\cdots A_{j}\), 用 \(m[i, j]\) 表示计算 \(A_{i..j}\) 所需标量乘法次数的最小值。则原问题的最优解即等价于求解 \(m[1, n]\)
- 递归公式为:
-
\[m[i, j]=\left\{\begin{array}{ll} \]
-
\min \limits_{i \leq k<j}\left{m[i, k]+m[k+1, j]+p_{i-1} p_{k} p_{j}\right} & \text { if } i<j
\end{array}\right.$$
- 为了构造最优解,需要使用 \(s[i, j]\) 来保存 \(A_{i..j}\) 的最优化括号方案的分割点位置 \(k\)
3. 计算最优代价
- 计算 \(m[i, j]\) 只用依赖于少于 \(j-i+1\) 个矩阵链相乘的最优计算代价
- 因此,采用自底向上法求解时,应按长度递增的顺序求解矩阵链括号化问题
代码实现
%%writefile ch15/matrix_chain.py
""""矩阵链乘法的动态规划算法"""
def matrix_chain_order(p):
"""计算矩阵链乘法所需要的最少标量乘法"""
length = len(p) - 1 # 矩阵链中矩阵的个数
m = [[ 0 for i in range(length)] for j in range(length)] # 存放 m[i, j] 的最优解
s = [[ 0 for i in range(length-1)] for j in range(length-1)] # 存放 m[i, j](i < j)最优解对应的分割点 k , 其中 m[i, j] 对应的值存放在 s[i, j-1] 中
for matrix_length in range(2, length+1):
for i in range(1, length - matrix_length + 2):
j = i + matrix_length - 1
m[i-1][j-1] = float('inf')
for k in range(i, j):
q = m[i-1][k-1] + m[k][j-1] + p[i-1]*p[k]*p[j]
if q < m[i-1][j-1]:
m[i-1][j-1] = q
s[i-1][j-2] = k
return m, s
Overwriting ch15/matrix_chain.py
import ch15.matrix_chain
from ch15.matrix_chain import matrix_chain_order
p = [30, 35, 15, 5, 10, 20, 25]
m, s = matrix_chain_order(p)
m
[[0, 15750, 7875, 9375, 11875, 15125],
[0, 0, 2625, 4375, 7125, 10500],
[0, 0, 0, 750, 2500, 5375],
[0, 0, 0, 0, 1000, 3500],
[0, 0, 0, 0, 0, 5000],
[0, 0, 0, 0, 0, 0]]
s
[[1, 1, 3, 3, 3],
[0, 2, 3, 3, 3],
[0, 0, 3, 3, 3],
[0, 0, 0, 4, 5],
[0, 0, 0, 0, 5]]
-
运行过程分析
4. 构造最优解
- 可以借助矩阵 \(s\) 中的信息,递归的输出最优化括号方案
%%writefile -a ch15/matrix_chain.py
def print_optimal_parents(s, i, j):
"""根据矩阵 s 中的信息,打印出最优化的括号方案"""
if i == j:
print("A{}".format(i), end="")
else:
print("(", end="")
print_optimal_parents(s, i, s[i-1][j-2])
print_optimal_parents(s, s[i-1][j-2]+1, j)
print(")", end="")
Appending to ch15/matrix_chain.py
imp.reload(ch15.matrix_chain)
from ch15.matrix_chain import print_optimal_parents, matrix_chain_order
p = [30, 35, 15, 5, 10, 20, 25]
m, s = matrix_chain_order(p)
print_optimal_parents(s, 1, len(p)-1)
((A1(A2A3))((A4A5)A6))
练习
15.2-1
import ch15.matrix_chain
imp.reload(ch15.matrix_chain)
from ch15.matrix_chain import print_optimal_parents, matrix_chain_order
p = [5, 10, 3, 12, 5, 50, 6]
m, s = matrix_chain_order(p)
print_optimal_parents(s, 1, len(p)-1)
((A1A2)((A3A4)(A5A6)))
m[0][-1]
2010
15.2-2
%%writefile -a ch15/matrix_chain.py
def matrix_chain_multiply(A, s, i, j):
"""计算矩阵链的乘积"""
if i == j:
return A[i-1]
l = matrix_chain_multiply(A, s, i, s[i-1][j-2])
r = matrix_chain_multiply(A, s, s[i-1][j-2]+1, j)
return [[ sum([l[i][k] * r[k][j] for k in range(len(l[0]))]) # 计算两个矩阵的乘积
for j in range(len(r[0]))]
for i in range(len(l))]
Appending to ch15/matrix_chain.py
import ch15.matrix_chain
imp.reload(ch15.matrix_chain)
from ch15.matrix_chain import print_optimal_parents, matrix_chain_order, matrix_chain_multiply
from functools import reduce
import numpy as np # 利用 numpy 判断计算结果是否正确
p = [5, 10, 3, 12, 5, 50, 6]
A = []
for index, item in enumerate(p[:-1], 1):
A.append(np.random.randint(0, 10, (item, p[index])))
m, s = matrix_chain_order(p)
(matrix_chain_multiply(A, s, 1, len(A)) == reduce(np.dot, A)).all()
True
15.2-3
-

-
递推公式如下:
-
\[P(n)=\left\{\begin{array}{ll} \]
-
\sum_{k=1}^{n-1} P(k) P(n-k) & \text { if } n \geq 2
\end{array}\right.$$
- 由递推公式可得: \(P(8) = 429 \ge 2 ^ 8 = 256\)
- 假设 \(\forall 8 \le k < n\), \(P(k) \ge 2^k\),可得:
-
\[P(n) = \sum_{k=1}^{n-1}{2^k * 2 ^{n-k}} = \sum_{k=1}^{n-1}{2^n} = (n-1)*2^n \ge 2^n \]
-
- 证毕
15.2-4
-

-
子问题图的顶点个数为:
-
\[\sum_{i=1}^{n}\sum_{j=i}^{n}{1} = n + n - 1 + \cdots + 1 = {n(n+1) \over 2} \]
-
-
对于 \(A_{i..j}\) 的矩阵链,其需求解的子问题数为 \(2(j-i)\),所以包含的边数为:
-
\[\begin{align} \]
&= \sum_{i=1}^{n-1}{i(i+1) = {n(n-1)(n+1) \over 3}} && 此处可通过归纳法证明
\end{align}$$ -
-
这些边连接一个问题所需要求解的子问题
15.2-5
-
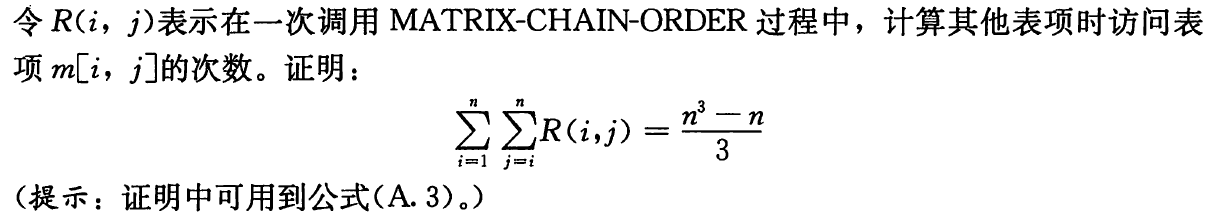
-
此问题的解即为问题 15.2-4 中的子问题图中的边的总数目
15.2-6
-

-
可通过归纳法进行证明
-
对于 \(n=1\),不需要进行括号化,需要 $n-1 = 0 $ 对括号,符合要求
-
假设 \(\forall 0 \le x \lt n\),其完全括号化需要 \(x-1\) 对括号
-
则当有 \(n\) 个元素时,在第 \(k\) 个元素添加括号,可得到完全括号化方案。则 \(A_{1..k}\) 有 \(k-2\) 对括号, \(A_{k+1..n}\) 有 \(n-k-1\) 对括号,在 \(k\) 处分割会引入两对括号,由此可得需要的总括号对数为:
-
\[(k-2) + (n - k - 1) + (2) = n - 1 \]
-
15.3 动态规划原理
最优子结构
- 用动态规划方法求解问题的第一步即是刻画最优解的结构
- 如果一个问题的最优解包含其子问题的最优解,就称此问题具有最优子结构的性质
- 在发掘最优子结构性质的过程中,遵循如下的通用模式
- 证明问题最优解的第一个组成部分是作出一个选择,做出这个选择会产生一个或多个待解的子问题
- 对于一个给定问题,在其可能的第一步选择中,假定已经知道哪种选择才会得到最优解
- 给定可获得最优解的选择后,确定这次选择会产生哪些子问题,以及如何最好地刻画子问题空间
- 利用“剪切一粘贴”(cut-and-paste)技术证明:作为构成原问题最优解的组成部分,每个子问题的解就是它本身的最优解
- 证明这一点是利用反证法:假定子问题的解不是其自身的最优解,那么就可以从原问题的解中“剪切”掉这些非最优解,将最优解“粘贴”进去,从而得到原问题一个更优的解,这与最初的解是原问题最优解的前提假设矛盾
- 如果原问题的最优解包含多个子问题,通常它们都很相似,可以将针对一个子问题的“剪切一粘贴”论证方法稍加修改,用于其他子问题
- 对于不同领域的问题,最优子结构主要体现在两个方面
- 原问题的最优解中涉及到多少个子问题
- 在确定最优解使用哪些子问题时,需要考察多少种选择
- 由这两个方面,也可以初步确定算法的运行时间
- 钢条切割问题有 \(\Theta(n)\) 个子问题,每个子问题有 \(O(n)\) 种选择,因此总的运行时间为 \(O(n^2)\)
- 矩阵链乘法问题有 \(\Theta(n^2)\) 个子问题,每个子问题有 \(O(n)\) 种选择,因此总运行时间为 \(O(n^3)\)
- 原问题最优解的代价通常等于其子问题最优解的代价再加上由于选择直接产生的代价
- 钢条切割问题每次选择产生的代价为 \(p_i\)
- 矩阵链乘法问题中,选择本身产生的代价为 \(p_{i-1}p_{k}p_{j}\)
- 子问题需要是无关的,才能满足最优子结构
- 子问题无关的含义是,同一个原问题的一个子问题的解不能影响另一个子问题的解
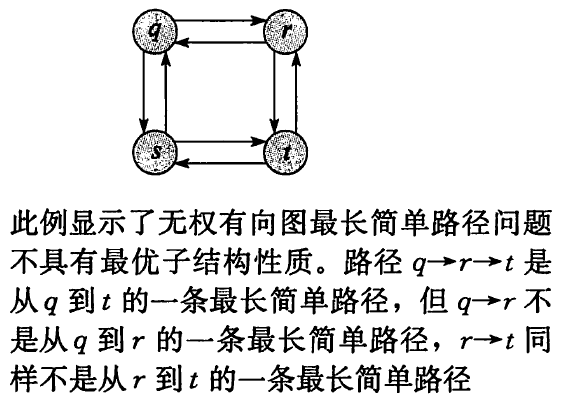
- 子问题相关的实例: 无权最长简单路径
-
重叠子问题
- 适合用动态规划方法求解的最优化问题应该具备的第二个性质是子问题的空间必须足够"小",这样问题的递归算法会反复的求解相同的子问题,而不是一直生成新的子问题
- 如果递归算法反复求解相同的子问题,就称最优化问题具有重叠子问题的性质
- 动态规划算法通常对每个子问题求解一次,将解存入一个表中,当再次需要这个子问题时直接查表,每次查表的代价为常量时间。
- 适合用分治方法求解的问题通常在递归的每一步都生成全新的子问题
重构最优解
- 通常将每个子问题所做的选择存入一个表中,这样就可以重构最优解
备忘
- 与自底向上的方法相比,可能不需要求解所有的子问题。但是递归调用会消耗额外的空间
练习题
15.3-1
-

-
RECURSIVE-MATRIX-CHAIN方法较优 -
对于 \(A_{1..n}\) 来说,假设 第 \(k\) 个元素是其最优的分割点
- 对于穷举法来说,其需要遍历 \(A_{1..k}\) 和 \(A_{k+1..n}\) 的所有可能的分割方法,然后将左右两边所有可能
的方法组合起来,得到最优的解。需要时间为\(O(k(n-k))\) - 对于递归法来说,其得到最优解只需对\(A_{1..k}\) 和 \(A_{k+1..n}\) 中的最优结果进行组合即可,需要时间为 \(O(1)\)
- 对于穷举法来说,其需要遍历 \(A_{1..k}\) 和 \(A_{k+1..n}\) 的所有可能的分割方法,然后将左右两边所有可能
15.3-2
-

-
递归调用树如下
-
-
备忘技术对分治算法无效,主要是因为分治算法每步产生的子问题都是新的子问题,想互之间不重叠
15.3-3
-

-
任然具有最优子结构的性质,假设 \(k\) 为 \(A_{1..n}\) 的最优分割点
-
则 \(A_{1..k}\) 和 \(A{k+1..n}\) 也需要为最大化矩阵序列括号化方案,才能得到总体的最大化矩阵序列括号化方案
- 可以通过 "剪切-粘贴法" 进行证明
15.3-4
-

-
设 \(p = [1000,100,20,10,1000]\)
-
则按照题述的方法,最优的括号化方案为 \(\left(\left(\left(A_{1} A_{2}\right) A_{3}\right) A_{4}\right)\)
- 所需的乘法次数为
-
\[1000 \cdot 100 \cdot 20+1000 \cdot 20 \cdot 10+1000 \cdot 10 \cdot 1000=12200000 \]
-
- 所需的乘法次数为
-
完全括号化方案为 \(\left(\left(A_{1}\left(A_{2} A_{3}\right)\right) A_{4}\right)\)
- 所需的乘法次数为
-
\[100 \cdot 20 \cdot 10+1000 \cdot 100 \cdot 10+1000 \cdot 10 \cdot 1000=11020000 \]
-
- 所需的乘法次数为
15.3-5
-

-
证明:
- 左边钢条的切割方案会影响右边钢条的切割方案,两个子问题不再相互独立,因此最优子结构的性质不再成立
15.3-6
-

-
佣金为 \(0\)
- 设 \(k\) 是从 \(1\) 到 \(n\) 进行兑换时所需要经过的中间货币,为了达到最大的收益,则从 \(1\) 到 \(k\) 和从 \(k\) 到 \(n\) 的货币兑换也需要获得最大收益,才能满足要求
- 可以通过“剪切-粘贴”法进行确认
- 设 \(k\) 是从 \(1\) 到 \(n\) 进行兑换时所需要经过的中间货币,为了达到最大的收益,则从 \(1\) 到 \(k\) 和从 \(k\) 到 \(n\) 的货币兑换也需要获得最大收益,才能满足要求
-
佣金 \(c_k\) 可能为任意值
- 此时会导致当 \(k\) 为中间货币时,左右两边的子问题不再相互独立,而是可能相互影响,因此不一定再具有最优子结构的性质
15.4 最长公共子序列
- 应用于 DNA 序列的相似度比较
相关概念
- 子序列
- 一个给定序列的子序列,就是将给定序列中的零个或多个元素去掉之后的结果
- 形式化定义: 给定一个序列 \(X = <x_1, x_2, \cdots, , x_m>\), 另一个序列 \(Z=<z_1, z_2, \cdots, z_k>\) 满足如下条件时称为 \(X\) 的子序列
- 存在一个严格递增的 \(X\) 的下标序列 \(<i_1, i_2, \cdots, i_k>\),对于所有的 \(j = 1, 2, \cdots, k\),满足 \(x_{i_j} = z_j\)
- 公共子序列
- 如果 \(Z\) 即是 \(X\) 的子序列,又是 \(Y\) 的子序列,则称 \(Z\) 是 \(X\) 和 \(Y\) 的公共子序列
- 最长公共子序列(longest-common-subsequence problem LCS),即是求两个序列 \(X\) 和 \(Y\) 的长度最长的公共子序列
1. 刻画最长公共子序列的特征
- LCS 的最优子结构
- 令 \(X= <x_1, x_2, \cdots, x_m>\) 和 \(Y=<y_1, y_2, \cdots, y_n>\) 为两个序列, \(Z = <z_1, z_2, \cdots, z_k>\) 为 \(X\) 和 \(Y\) 的任意 LCS
- 如果 \(x_m = y_n\),则 \(z_k = x_m = y_n\) 且 \(Z_{k-1}\) 是 \(X_{m-1}\) 和 \(Y_{m-1}\) 的一个 LCS
- 如果 \(x_m \neq y_n\),那么 \(z_k \neq x_m\) 意味着 \(Z\) 是 \(X_{m-1}\) 和 \(Y\) 的一个 LCS
- 如果 \(x_m \neq y_n\),那么 \(z_k \neq y_n\) 意味着 \(Z\) 是 \(X\) 和 \(Y_{n-1}\) 的一个 LCS
- 证明可以采用剪切-粘贴法
- 令 \(X= <x_1, x_2, \cdots, x_m>\) 和 \(Y=<y_1, y_2, \cdots, y_n>\) 为两个序列, \(Z = <z_1, z_2, \cdots, z_k>\) 为 \(X\) 和 \(Y\) 的任意 LCS
2. 一个递归解
- 由 LCS 的最优子结构,可得如下性质
- \(c[i, j]\) 表示 \(X_i\) 和 \(Y_j\) 的 LCS 长度
-
\[c[i, j] = \left\{ \begin{align} &0 && i= 0 或 j=0 \\ &c[i-1, j-1] + 1 && i,j > 0 且 x_i = y_j \\ &max(c[i, j-1], c[i-1, j]) && i,j > 0 且 x_i \neq y_i \]
- 在递归公式中,通过限制条件限定了需要求解哪类子问题
3. 计算 LCS 的长度
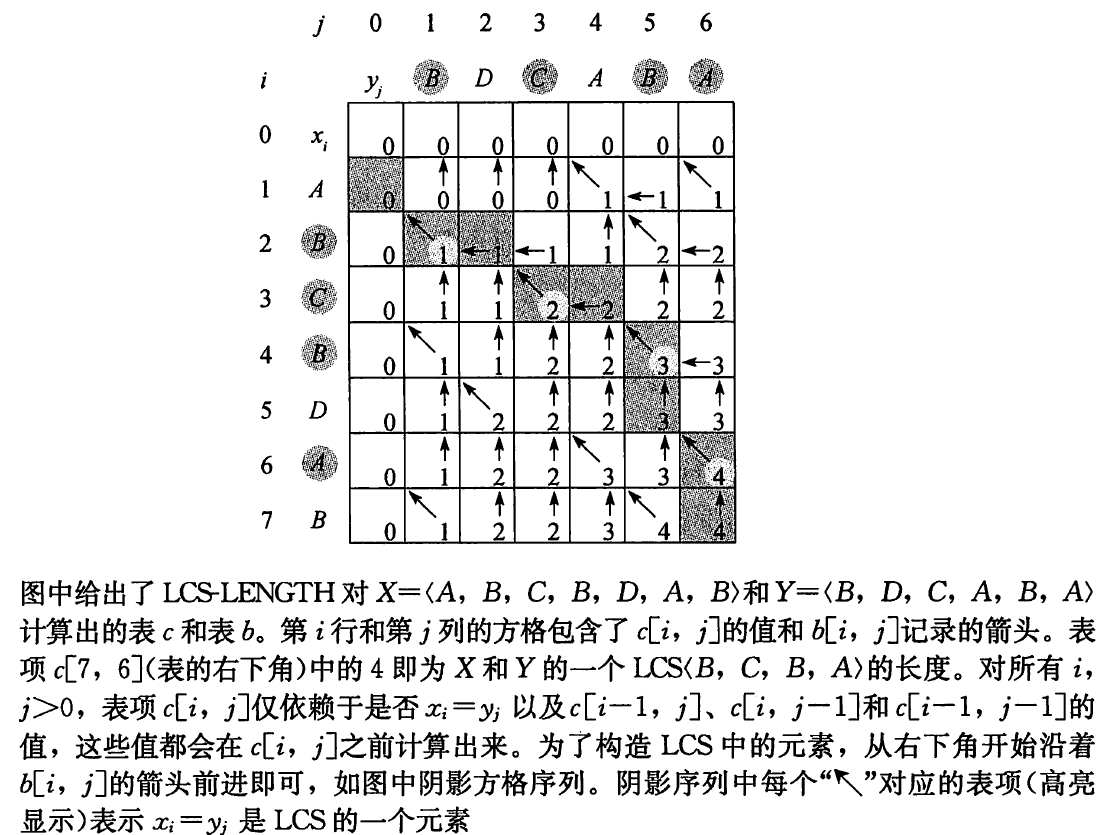
- 将 \(c[i, j]\) 的值保存在表 \(c[0..m, 0..n]\),并按行主次序计算表项
- 为了构造最优解,维护另一个表项 \(b[1..m, 1..n]\) ,其中 \(b[i, j]\) 对应计算 \(c[i, j]\) 时所选择的子问题的最优解
%%writefile ch15/lcs.py
"""最长公共子序列问题"""
def lcs_length(X, Y):
"""求两个序列的最长公共子序列"""
m, n = len(X), len(Y)
c = [[0]*(n+1) for i in range(m+1)]
b = [[None]*n for i in range(m)]
for i in range(1, m+1):
for j in range(1, n+1):
if X[i-1] == Y[j-1]:
c[i][j] = c[i-1][j-1] + 1
b[i-1][j-1] = '↖'
elif c[i-1][j] >= c[i][j-1]:
c[i][j] = c[i-1][j]
b[i-1][j-1] = '↑'
else:
c[i][j] = c[i][j-1]
b[i-1][j-1] = '←'
return c, b
Overwriting ch15/lcs.py
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import lcs_length
X = ['A', 'B', 'C', 'B', 'D', 'A', 'B']
Y = ['B', 'D', 'C', 'A', 'B', 'A']
c, b = lcs_length(X, Y)
c
[[0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 1, 1],
[0, 1, 1, 1, 1, 2, 2],
[0, 1, 1, 2, 2, 2, 2],
[0, 1, 1, 2, 2, 3, 3],
[0, 1, 2, 2, 2, 3, 3],
[0, 1, 2, 2, 3, 3, 4],
[0, 1, 2, 2, 3, 4, 4]]
b
[['↑', '↑', '↑', '↖', '←', '↖'],
['↖', '←', '←', '↑', '↖', '←'],
['↑', '↑', '↖', '←', '↑', '↑'],
['↖', '↑', '↑', '↑', '↖', '←'],
['↑', '↖', '↑', '↑', '↑', '↑'],
['↑', '↑', '↑', '↖', '↑', '↖'],
['↖', '↑', '↑', '↑', '↖', '↑']]
- 具体执行过程:
-
4. 构造 LCS
- 可以根据表 \(b\) 中的信息,来构造出 LCS
- 当在 \(b\) 中碰到一个 “↖” 时, 意味着碰到了 LCS 中的一个元素
%%writefile -a ch15/lcs.py
def print_LCS(b, X, i, j):
"""打印出最长公共子序列"""
if i == 0 or j == 0:
return
if b[i-1][j-1] == '↖':
print_LCS(b, X, i-1, j-1)
print(X[i-1], end=" ")
elif b[i-1][j-1] == '↑':
print_LCS(b, X, i-1, j)
else:
print_LCS(b, X, i, j-1)
Appending to ch15/lcs.py
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import lcs_length, print_LCS
X = ['A', 'B', 'C', 'B', 'D', 'A', 'B']
Y = ['B', 'D', 'C', 'A', 'B', 'A']
c, b = lcs_length(X, Y)
print_LCS(b, X, len(X), len(Y))
B C B A
算法改进
- 可以去掉表 \(b\),因为在不改变渐近运行时间的前提上,借助表 \(c\) 也能判断出箭头的方向
- 因为每个 \(c[i, j]\) 只依赖于表 \(c\) 中的其他三项, \(c[i-1, j], c[i, j-1], c[i-1, j-1]\),可在在 \(O(1)\) 的时间内判断出计算 \(c[i, j]\) 时用到了这三项中的哪一个
- 可以减小空间占用,但并未渐近的减少计算 LCS 所需的辅助空间
- 如果不需要重构 LCS 序列,只需要保留表 \(c\) 中的两行即可(当前正在计算的一行和前一行)
练习
15.4-1
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import lcs_length, print_LCS
X = [1, 0, 0, 1, 0, 1, 0, 1]
Y = [0, 1, 0, 1, 1, 0, 1, 1, 0]
c, b = lcs_length(X, Y)
print_LCS(b, X, len(X), len(Y))
1 0 0 1 1 0
15.4-2
%%writefile -a ch15/lcs.py
def print_LCS_without_b(c, X, Y, i, j):
"""15.4-2: 在没有表 b 的情况下输出最长公共子序列"""
if i == 0 or j == 0:
return
if c[i][j] == c[i-1][j-1] + 1:
print_LCS_without_b(c, X, Y, i-1, j-1)
print(X[i-1], end=' ')
elif c[i][j] == c[i-1][j]:
print_LCS_without_b(c, X, Y, i-1, j)
else:
print_LCS_without_b(c, X, Y, i, j-1)
Appending to ch15/lcs.py
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import lcs_length, print_LCS_without_b
X = [1, 0, 0, 1, 0, 1, 0, 1]
Y = [0, 1, 0, 1, 1, 0, 1, 1, 0]
c, b = lcs_length(X, Y)
print_LCS_without_b(c, X, Y, len(X), len(Y))
1 0 1 0 1 1
15.4-3
%%writefile -a ch15/lcs.py
def memoized_lcs_length(X, Y):
"""15.4-3: 带备忘的 lcs 算法"""
m, n = len(X), len(Y)
c = [[None] * (n+1) for i in range(m+1)]
b = [[None]* n for i in range(m)]
memoized_lcs_length_aux(X, Y, len(X), len(Y), c, b)
return c, b
def memoized_lcs_length_aux(X, Y, i, j, c, b):
"""带备忘的 lcs 算法的辅助函数"""
if i == 0 or j == 0:
return 0
if X[i-1] == Y[j-1]:
c[i][j] = 1 + memoized_lcs_length_aux(X, Y, i-1, j-1, c, b)
b[i-1][j-1] = '↖'
else:
up = memoized_lcs_length_aux(X, Y, i-1, j, c, b)
left = memoized_lcs_length_aux(X, Y, i, j-1, c, b)
b[i-1][j-1], c[i][j] = ('↑', up) if up >= left else ('←', left)
return c[i][j]
Appending to ch15/lcs.py
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import memoized_lcs_length, print_LCS
X = ['A', 'B', 'C', 'B', 'D', 'A', 'B']
Y = ['B', 'D', 'C', 'A', 'B', 'A']
c, b = memoized_lcs_length(X, Y)
print_LCS(b, X, len(X), len(Y))
B C B A
b
[['↑', '↑', '↑', '↖', None, None],
['↖', '←', '←', '↑', None, None],
['↑', '↑', '↖', '←', None, None],
['↖', '↑', '↑', '↑', '↖', None],
[None, '↖', '↑', '↑', '↑', None],
[None, None, None, '↖', None, '↖'],
[None, None, None, None, '↖', '↑']]
c
[[None, None, None, None, None, None, None],
[None, 0, 0, 0, 1, None, None],
[None, 1, 1, 1, 1, None, None],
[None, 1, 1, 2, 2, None, None],
[None, 1, 1, 2, 2, 3, None],
[None, None, 2, 2, 2, 3, None],
[None, None, None, None, 3, None, 4],
[None, None, None, None, None, 4, 4]]
- 从 \(b, c\) 数组的值可看出,带备忘的算法并没有计算所有的子问题
15.4-4
-

-
每次计算 \(c[i, j]\) 时,只需要利用 \(c[i-1, j-1], c[i-1, j], c[i, j-1]\) 这三个值即可,因此可以只储存之前一行和当前计算行的信息,便可完成计算
- 所需表项的长度为 \(2 \times min(m, n)\)
- 设每行的元素数为 \(x\),则按行主次序计算 \(c\) 时 \(c[i,j]\) 与 \(c[i-1, j-1]\) 之间相差 \(x\) 个元素,与 \(c[i-1, j]\) 之间相差 \(x-1\) 个元素,与 \(c[i][j-1]\) 之间相差 \(0\) 个元素
- 由此可以使用一个长为 \(x\) 的队列,储存计算 \(c[i, j]\) 所需要的信息
- 实际程序编写时,需要注意一些边界条件
%%writefile -a ch15/lcs.py
from collections import deque
def lcs_length_queue(X, Y):
"""15.4-4: 借助队列来减小表项所需的额外空间"""
m, n = len(X), len(Y)
if m < n:
m, n = n, m
X, Y = Y, X
dq = deque(maxlen=n)
a = 0 # 初始时的 c[i-1][j-1]
for i in range(m):
for j in range(n):
if X[i] == Y[j]:
b = a + 1 if j != 0 else 1 # b 为 c[i][j]
a = dq.popleft() if i != 0 else 0 # 下一次循环时的 c[i-1][j-1]
dq.append(b)
else:
a = dq.popleft() if i != 0 else 0 # 此次循环的 c[i-1][j], 下一次循环的 c[i-1][j-1]
d = dq[-1] if j != 0 else 0 # c[i][j-1]
dq.append(max(a, d))
return dq[-1]
Appending to ch15/lcs.py
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import lcs_length_queue
X = ['A', 'B', 'C', 'B', 'D', 'A', 'B']
Y = ['B', 'D', 'C', 'A', 'B', 'A']
lcs_length_queue(X, Y)
4
X = [1, 0, 0, 1, 0, 1, 0, 1]
Y = [0, 1, 0, 1, 1, 0, 1, 1, 0]
lcs_length_queue(X, Y)
6
15.4-5
-
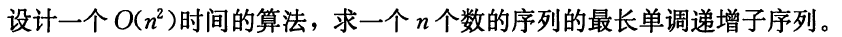
-
设序列为 \(X\),将 \(X\) 中的元素按递增的顺序排列得到序列 \(Y\), 则 \(X\) 与 \(Y\) 的最大公共子序列即为 \(X\) 中最长的单调递增子序列
%%writefile -a ch15/lcs.py
def longest_increasing_subsequence_by_LCS(X):
"""15.4-5: 在 O(n^2) 的时间内求一个序列的最长单调递增子序列"""
Y = sorted(X)
c, b = memoized_lcs_length(X, Y)
print_LCS(b, X, len(X), len(Y))
Appending to ch15/lcs.py
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import longest_increasing_subsequence_by_LCS
X = list(range(10))
random.shuffle(X)
print(X, "中的最长单调递增子序列为: ")
longest_increasing_subsequence_by_LCS(X)
[8, 5, 7, 4, 1, 2, 6, 9, 3, 0] 中的最长单调递增子序列为:
1 2 6 9
15.4-6
-

-
提示描述的有问题,应为:
- 长度为 \(i\) 的子序列中的最小尾元素至少不小于长度为 \(i-1\) 的候选子序列的尾元素
- 证明可通过反证法实现
-
算法描述
- 可构造一个长度为 \(n\) 的序列 \(s[1..n]\),初始时所有元素均赋值为 \(+\infty\), \(n\) 为待求解序列 \(X\) 的长度
- \(s[j](s[j] \neq +\infty)\) 表示长度为 \(j\) 的单调递增序列中最小的尾元素
- 依次遍历 \(X\) 中的元素, 第 \(i\) (\(i= 1, 2, \cdots, n\))次遍历时
- 如果 \(X[i] < s[1]\),则令 \(s[1]=X[i]\)
- 否则,借助二分法查找最大的 \(j\),使得 \(s[j] < X[i]\), 进行赋值操作 \(s[j+1] = X[i]\)
- 此时,可证明 \(s[j](s[j] \neq + \infty)\) 是 \(X[1..i]\) 中长度为 \(j\) 的单调递增序列中的最小尾元素
- \(s\) 中不为 \(+\infty\) 的元素数量,即为最长单调递增子序列的长度,设最长长度为 \(k\)
- 构造最长单调递增子序列
- 在 \(s\) 的未尾追加一个元素 \(+\infty\)
- 令 \(i=k\),逆序遍历 \(X\) 中的元素
- 找出一个元素 \(x\) 满足 $ s[i] \le x \le s[i+1]$,然后将 \(i\) 自减 \(1\),继续遍历,直至 \(i\) 为 \(0\)
- 如果 \(A[1, k]\) 中包含长度为 \(i\) 的单调递增序列,则其也一定包含长度为 \(i-1\) 的递增序列,由此性质可知 \(x\) 一定存在
- 找出一个元素 \(x\) 满足 $ s[i] \le x \le s[i+1]$,然后将 \(i\) 自减 \(1\),继续遍历,直至 \(i\) 为 \(0\)
- 将遍历得到的元素逆序输出,即为一个最长单调递增子序列
- 可构造一个长度为 \(n\) 的序列 \(s[1..n]\),初始时所有元素均赋值为 \(+\infty\), \(n\) 为待求解序列 \(X\) 的长度
%%writefile ch15/longest_increasing_subsequence.py
from bisect import bisect
def longest_increasing_subsequence(X):
"""15.4-6: 在 O(nlgn) 的时间内求解一个序列的最长单调递增子序列"""
s = [float('inf')] * len(X)
L = 0 # s 中非 inf 的元素数目
for i in range(len(X)):
j = bisect(s, X[i])
s[j] = X[i]
if j + 1 > L:
L = j + 1
res = [None] * L
k = len(X)
s.append(float('inf'))
for i in reversed(range(L)):
while k > 0:
k -= 1
if s[i+1] >= X[k] >= s[i]:
res[i] = X[k]
break
return res
Overwriting ch15/longest_increasing_subsequence.py
import ch15.longest_increasing_subsequence
imp.reload(ch15.longest_increasing_subsequence)
from ch15.longest_increasing_subsequence import longest_increasing_subsequence
X = list(range(10))
random.shuffle(X)
# X = [1, 2, 3, 4, 1, 2, 5, 4]
print(X, "中的最长单调递增子序列为: ", longest_increasing_subsequence(X))
[0, 4, 7, 2, 3, 5, 9, 8, 6, 1] 中的最长单调递增子序列为: [0, 2, 3, 5, 6]
15.5 最优二叉搜索树
- 实际应用: 英语到法语的翻译
最优二叉搜索树的问题描述
- 给定 \(n\) 个不同关键字的已排序序列 \(K=<k_1, k_2, \cdots, k_n>\), 希望用这些关键字构造一棵二叉搜索树
- 对于每一个关键字 \(k_i\),都有一个概率 \(p_i\) 表示其搜索频率
- 有些要搜索的值可能不在 \(K\) 中, 因此还有 \(n+1\) 个 “伪关键字” \(d_0, d_1, d_2, \cdots, d_n\) 表示不在 \(K\) 中的值
- \(d_0\) 表示所有小于 \(k_1\) 的值, \(d_n\) 表示所有大于 \(k_n\) 的值
- \(d_i, i= 1, 2, \cdots, n-1\) 表示所有在 \(k_i\) 和 \(k_{i+1}\) 之间的值
- 对于每一个 \(d_i\),也都有一个概率 \(q_i\) 表示其搜索频率
- 每次搜索要么成功,要么失败,有下式成立: $$\sum_{i=1}^{n} p_{i}+\sum_{i=0}^{n} q_{i}=1$$
- 示例
-
- 在树 \(T\) 中进行一次搜索的期望代价为
-
\[\begin{align} \]
-
&=1+\sum_{i=1}^{n} \operatorname{depth}{T}\left(k\right) \cdot p_{i}+\sum_{i=0}^{n} \operatorname{depth}{T}\left(d\right) \cdot q_{i}
\end{align}$$
- 从图中可看出,最优二叉搜索树不一定是最矮的,概论最高的关键字也不一定出现在根结点
- 对于一个给定的概率集合,希望构建一颗期望代价最小的二叉搜索树,称之为最优二叉搜索树
1. 最优二叉搜索树的结构
- 子树的特征
- 一棵二叉搜索树 \(T\) 的任意子树必须包含连续关键字 \(k_i, \cdots, k_j, 1 \le i \le j \le n\),而且其叶结点必然是伪关键字 \(d_{i-1}, \cdots, d_j\)
- 最优子结构
- 如果一棵最优的二叉搜索树 \(T\) 有一棵包含 \(k_{i}, \dots, k_{j}\)的子树 \(T^{\prime}\), 那么 \(T^{\prime}\) 必然是包含关键字\(k_i, \cdots, k_j\) 和伪关键字 \(d_{i-1}, \cdots, d_j\) 的子问题的最优解
- 证明可采用剪切-粘贴法
- 空子树
- 对于包含关键字 \(k_i, \cdots, k_j\) 的子问题
- 如果选定 \(k_i\) 为根结点,\(k_i\) 的左子树不包含任何实际关键字,只包含单一伪关键字 \(d_{i-1}\)
- 如果选定 \(k_j\) 为根结点,则 \(k_j\) 的右子村不包含任何实际关键字,只包含单一伪关键字 \(d_{j}\)
- 对于包含关键字 \(k_i, \cdots, k_j\) 的子问题
2. 递归算法
- 对于包含关键字 \(k_i, \cdots, k_j\) 的子树,所有的概率之和为:
-
\[w(i, j)=\sum_{l=i}^{j} p_{l}+\sum_{l=i-1}^{j} q_{l} \]
-
- 若 \(k_r\) 为包含关键字 \(k_i, \cdots, k_j\) 的最优二叉搜索树的根结点,可得
-
\[e[i, j]=p_{r}+(e[i, r-1]+w(i, r-1))+(e[r+1, j]+w(r+1, j)) \]
- 代入: \(w(i, j)=w(i, r-1)+p_{r}+w(r+1, j)\) 可得:
-
\[e[i, j]=e[i, r-1]+e[r+1, j]+w(i, j) \]
-
- 由此可得计算 \(e[i, j]\) 的递推公式为
-
\[e[i, j]=\left\{\begin{array}{ll} \]
-
\min _{i \leq r \leq j}{e[i, r-1]+e[r+1, j]+w(i, j)} & \text { if } i \leq j
\end{array}\right.$$
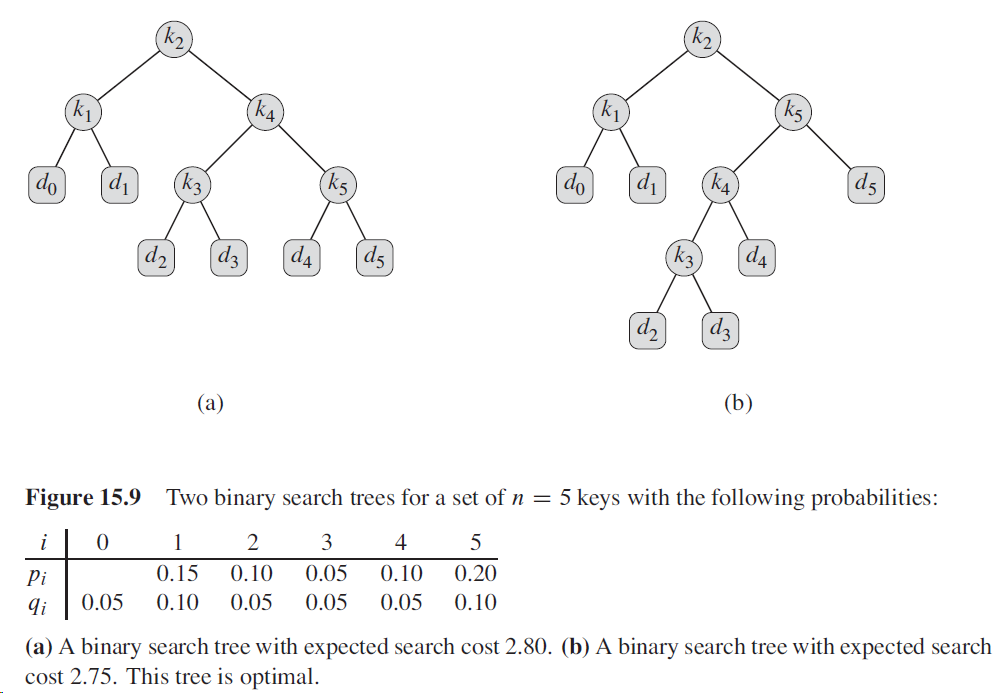
3. 计算最优二叉搜索树的期望搜索代价
- 用表 \(e[1..n+1, 0..n]\) 来保存 \(e[i, j]\) 的值
- \(i, j\) 对应的数组下标不同,因为还要计算空子树的值
- 用表 \(root[1..n, 1..n]\) 来储存包含关键字 \(k_i, .. k_j\) 的最优二叉搜索树的根
- 可以用另外一张表 \(w[1..n+1, 0..n]\) 来储存 \(w[i, j]\) 的值,可按下式加速计算
-
\[w[i, j]=w[i, j-1]+p_{j}+q_{j} \]
-
%%writefile ch15/optimal_bst.py
""""计算最优二叉搜索树"""
def optimal_bst(p, q):
n = len(p)
e = [[ q[i-1] if (i-1) == j else float('inf') for i in range(1, n+2)] for j in range(n+1)]
w = [[ q[i-1] if (i-1) == j else 0 for i in range(1, n+2)] for j in range(n+1)]
root = [[0] * n for i in range(n)]
for l in range(1, n+1):
for i in range(1, n-l+2):
j = i + l - 1
w[i-1][j] = w[i-1][j-1] + p[j-1] + q[j]
for k in range(i, j+1):
t = e[i-1][k-1] + e[k][j] + w[i-1][j]
if t < e[i-1][j]:
e[i-1][j] = t
root[i-1][j-1] = k
return e, root
Overwriting ch15/optimal_bst.py
import ch15.optimal_bst
imp.reload(ch15.optimal_bst)
from ch15.optimal_bst import optimal_bst
p = [0.15, 0.10, 0.05, 0.10, 0.20]
q = [0.05, 0.10, 0.05, 0.05, 0.05, 0.10]
e, root = optimal_bst(p, q)
e
[[0.05, 0.45000000000000007, 0.9, 1.25, 1.75, 2.75],
[inf, 0.1, 0.4, 0.7, 1.2, 2.0],
[inf, inf, 0.05, 0.25, 0.6, 1.2999999999999998],
[inf, inf, inf, 0.05, 0.30000000000000004, 0.9],
[inf, inf, inf, inf, 0.05, 0.5],
[inf, inf, inf, inf, inf, 0.1]]
root
[[1, 1, 2, 2, 2],
[0, 2, 2, 2, 4],
[0, 0, 3, 4, 5],
[0, 0, 0, 4, 5],
[0, 0, 0, 0, 5]]
- 运行过程分析
-
复杂度分析
- 最优二叉搜索树的运行过程与矩阵链乘法基本相同,时间复杂度也为 \(\Theta(n^3)\)
练习
15.5-1
-

-
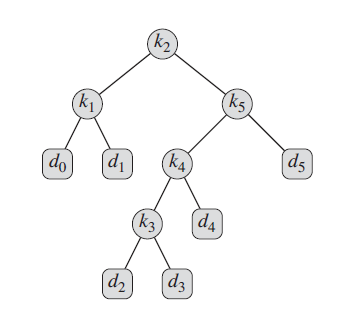
-
相当于中序遍历
%%writefile -a ch15/optimal_bst.py
def construct_optimal_bst(root):
"""15.5-1: 构造最优二叉搜索树"""
m, n = len(root), len(root[0])
print("k{} 为根".format(root[0][n-1]))
construct_optimal_bst_aux(root, 1, n)
def construct_optimal_bst_aux(root, i, j):
"""构造最优二叉搜索树的辅助函数"""
r = root[i-1][j-1]
if i == j:
print("d{} 为 k{} 的左孩子".format(r-1, r))
print("d{} 为 k{} 的右孩子".format(r, r))
return
if i == r:
print("d{} 为 k{} 的左孩子".format(r-1, r-1))
else:
print("k{} 为 k{} 的左孩子".format(root[i-1][r-2], r))
construct_optimal_bst_aux(root, i, r-1)
if j == r:
print("d{} 为 d{} 的右孩子".format(r, r))
else:
print("k{} 为 k{} 的右孩子".format(root[r][j-1], r))
construct_optimal_bst_aux(root, r+1, j)
Appending to ch15/optimal_bst.py
import ch15.optimal_bst
imp.reload(ch15.optimal_bst)
from ch15.optimal_bst import optimal_bst, construct_optimal_bst
p = [0.15, 0.10, 0.05, 0.10, 0.20]
q = [0.05, 0.10, 0.05, 0.05, 0.05, 0.10]
e, root = optimal_bst(p, q)
construct_optimal_bst(root)
k2 为根
k1 为 k2 的左孩子
d0 为 k1 的左孩子
d1 为 k1 的右孩子
k5 为 k2 的右孩子
k4 为 k5 的左孩子
k3 为 k4 的左孩子
d2 为 k3 的左孩子
d3 为 k3 的右孩子
d4 为 d4 的右孩子
d5 为 d5 的右孩子
15.5-2
import ch15.optimal_bst
imp.reload(ch15.optimal_bst)
from ch15.optimal_bst import optimal_bst, construct_optimal_bst
p = [0.04, 0.06, 0.08, 0.02, 0.10, 0.12, 0.14]
q = [0.06, 0.06, 0.06, 0.06, 0.05, 0.05, 0.05, 0.05]
e, root = optimal_bst(p, q)
print("期望代价为:", e[0][-1])
期望代价为: 3.12
construct_optimal_bst(root)
k5 为根
k2 为 k5 的左孩子
k1 为 k2 的左孩子
d0 为 k1 的左孩子
d1 为 k1 的右孩子
k3 为 k2 的右孩子
d2 为 k2 的左孩子
k4 为 k3 的右孩子
d3 为 k4 的左孩子
d4 为 k4 的右孩子
k7 为 k5 的右孩子
k6 为 k7 的左孩子
d5 为 k6 的左孩子
d6 为 k6 的右孩子
d7 为 d7 的右孩子
15.5-3
-

-
公式 (15.12) 如下:
-
\[w(i, j)=\sum_{l=i}^{j} p_{l}+\sum_{l=i-1}^{j} q_{l} \]
-
-
每次计算的时间代价为 \(O(n)\),因此不会影响渐近时间复杂性
15.5-4
代码实现
%%writefile -a ch15/optimal_bst.py
def improved_optimal_bst(p, q):
"""15.5-4: 改进最优二叉搜索树算法"""
n = len(p)
e = [[ q[i-1] if (i-1) == j else float('inf') for i in range(1, n+2)] for j in range(n+1)]
w = [[ q[i-1] if (i-1) == j else 0 for i in range(1, n+2)] for j in range(n+1)]
root = [[0] * n for i in range(n)]
for l in range(1, n+1):
for i in range(1, n-l+2):
j = i + l - 1
w[i-1][j] = w[i-1][j-1] + p[j-1] + q[j]
if i != j:
r = range(root[i-1][j-2], root[i][j-1]) # 利用相关的结论
else:
r = range(i, j+1)
for k in range(i, j+1):
t = e[i-1][k-1] + e[k][j] + w[i-1][j]
if t < e[i-1][j]:
e[i-1][j] = t
root[i-1][j-1] = k
return e, root
Appending to ch15/optimal_bst.py
import ch15.optimal_bst
imp.reload(ch15.optimal_bst)
from ch15.optimal_bst import improved_optimal_bst
p = [0.15, 0.10, 0.05, 0.10, 0.20]
q = [0.05, 0.10, 0.05, 0.05, 0.05, 0.10]
e, root = improved_optimal_bst(p, q)
e
[[0.05, 0.45000000000000007, 0.9, 1.25, 1.75, 2.75],
[inf, 0.1, 0.4, 0.7, 1.2, 2.0],
[inf, inf, 0.05, 0.25, 0.6, 1.2999999999999998],
[inf, inf, inf, 0.05, 0.30000000000000004, 0.9],
[inf, inf, inf, inf, 0.05, 0.5],
[inf, inf, inf, inf, inf, 0.1]]
root
[[1, 1, 2, 2, 2],
[0, 2, 2, 2, 4],
[0, 0, 3, 4, 5],
[0, 0, 0, 4, 5],
[0, 0, 0, 0, 5]]
复杂度分析
- 第 2 层循环所有的时间代价为 \(\Theta(n)\),因为修改后的第三层循环,互不重叠
- 假设 \(i, l\) 不变,此次循环,第三层循环的界为 \(root[i, j-1] \le root[i, j] \le root[i+1, j]\)
- 下次循环时, \(i, j\) 均增加 \(1\),第三层循环的下界为 \(root[i+1, j] \le root[i+1, j+1] \le root[i+2, j+1]\)
- 由于\(root[i,j]\) 的值在 \([1, n]\) 之间,因此第二层循环的时间复杂度为 \(\Theta(n)\)
- 由此可得整体的运行时间减为 \(\Theta(n^2)\)
思考题
15-1 有向无环图中的最长简单路径
-

-
涉及到图论的相关知识,学完图后再回来补
15-2 最长回文子序列
借助 LCS 算法
- 一种方式是直接借助 LCS 算法
- 设待求的序列为 \(X\),其逆序序列为 \(Y\),则 \(X, Y\) 的 LCS 即为 \(X\) 中的最长回文子序列
- 设 \(X\) 的长度为 \(n\),则此算法的时间复杂度为 \(O(n^2)\)
import ch15.lcs
imp.reload(ch15.lcs)
from ch15.lcs import lcs_length, print_LCS
X = 'character'
Y = X[::-1]
c, b = lcs_length(X, Y)
print_LCS(b, X, len(X), len(Y))
c a r a c
针对本问题的动态规划算法
- 如果要求序列 \(A[1..n]\) 的最长回文字序列,可以借助 \(A[2..n-1]\) 的最长回文序列来确定,具体如下:
-
\[c[i, j] = \left\{ \begin{align} &A[i] &&& if\ i == j\\ &A[i] + c[i+1, j-1] +A[j] &&& if\ i \neq j \ and \ A[i] == A[j]\\ &c[i+1, j], c[i, j-1] 中的最长子序列 &&& if\ i \neq j \ and \ A[i] \neq A[j] \end{align} \right.\]
- \(i\le j\)
- \(c[i,j]\) 表示 \(A[i..j]\) 的最长回文子序列
-
储存 \(A[i,j]\) 最长回文子序列
%%writefile ch15/longest_palindrome_subsequence.py
"""15-2 最长回文子序列"""
def longest_palindrome_subsequence(X):
"""空间复杂度为 O(n^3)"""
n = len(X)
c = [['' if i!=j else X[i] for j in range(n)] for i in range(n)]
for l in range(2, n+1):
for i in range(1, n-l+2):
j = i + l - 1
if X[i-1] == X[j-1]:
c[i-1][j-1] = X[i-1] + c[i][j-2] + X[j-1]
else:
c[i-1][j-1] = c[i][j-1] if len(c[i][j-1]) > len(c[i-1][j-2]) else c[i-1][j-2]
return c[0][n-1]
Overwriting ch15/longest_palindrome_subsequence.py
import ch15.longest_palindrome_subsequence
imp.reload(ch15.longest_palindrome_subsequence)
from ch15.longest_palindrome_subsequence import longest_palindrome_subsequence
X = 'character'
longest_palindrome_subsequence(X)
'carac'
- 此种算法,时间复杂度为 \(O(n^2)\)
- 由于 \(c[i, j]\) 的长度最大为 \(j-i+1\),所以空间复杂度为 \(O(n^3)\),占用空间较大,可进一步优化
\(c[i, j]\) 储存 \(A[i, j]\) 的最长子序列的长度,然后根据 \(c[i, j]\) 的信息重构生成最长回文子序列
- 此时 \(c[i, j]\) 的计算公式如下:
-
\[c[i, j] = \left\{ \begin{align} &1 &&& if\ i == j\\ &c[i+1, j-1] + 2 &&& if\ i \neq j \ and \ A[i] == A[j]\\ &max(c[i+1, j], c[i, j-1]) &&& if\ i \neq j \ and \ A[i] \neq A[j] \end{align} \right.\]
-
%%writefile -a ch15/longest_palindrome_subsequence.py
def improved_longest_palindrome_subsequence(X):
"""空间复杂度为 O(n^2)"""
n = len(X)
c = [[0 if i!=j else 1 for j in range(n)] for i in range(n)]
# 计算 c 的值
for l in range(2, n+1):
for i in range(1, n-l+2):
j = i + l - 1
if X[i-1] == X[j-1]:
c[i-1][j-1] = c[i][j-2] + 2
else:
c[i-1][j-1] = max(c[i][j-1], c[i-1][j-2])
# 重构最长的回文子序列
i, j = 1, n
res = ''
while i < j:
if X[i-1] == X[j-1]:
res = X[i-1] + res
i += 1
j -= 1
elif c[i][j-1] > c[i-1][j-2]:
i += 1
else:
j -= 1
return res[::-1] + X[i-1] + res if i == j else res[::-1] + res
Appending to ch15/longest_palindrome_subsequence.py
import ch15.longest_palindrome_subsequence
imp.reload(ch15.longest_palindrome_subsequence)
from ch15.longest_palindrome_subsequence import improved_longest_palindrome_subsequence
X = 'character'
improved_longest_palindrome_subsequence(X)
'carac'
- 重构最长回文子序列的时间复杂度为 \(O(n)\),因此程序总体的时间复杂度仍为 \(O(n^2)\),但是空间复杂度降低到 \(O(n^2)\)
15-3 双调欧几里得旅行商问题
-
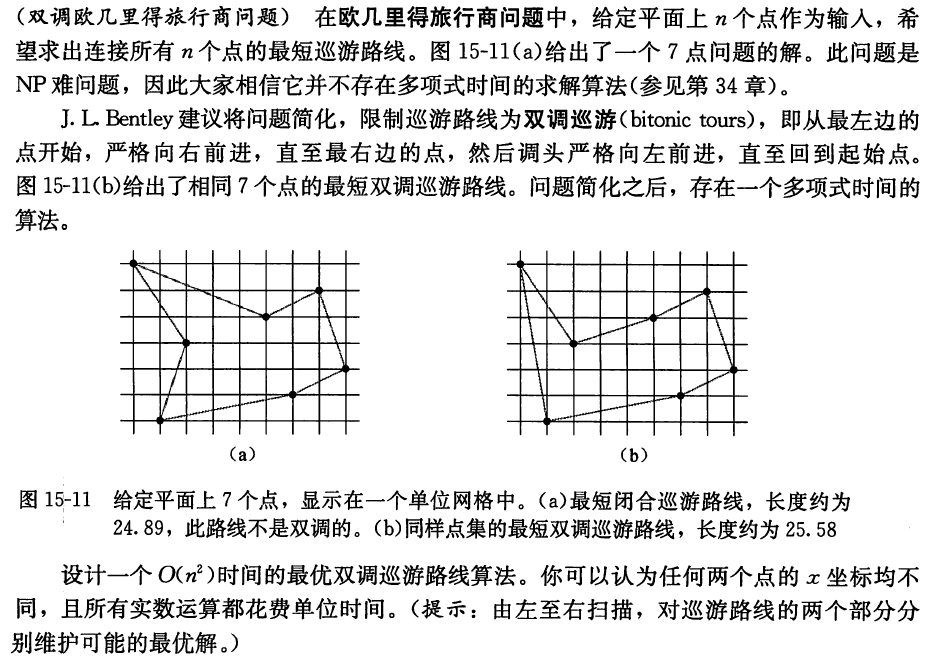
-
将 \(n\) 个点按 \(x\) 轴坐标进行排序, \(i(i = 1, 2, \cdots, n)\) 表示排序后第 \(i\) 个位置的坐标点
-
\(d[i, j]\) 表示第一条路线的终点为 \(i\), 第二条路线的终点为 \(j\) 时,巡游路线的最小值, 由于两条路线的对称性,不妨设 \(i \le j\)
-
\(j \gt 2\) 时,\(d[i, j]\) 可按以下递推式求得:
-
\[d[i, j] = \left\{ \begin{align} &d[i, j - 1] + P_{(j-1)j} && \ if \ i < j - 1\\ &\min\limits_{1\le u \lt j-1}{\{d[u, j-1] + P_{uj}\} } && \ if \ i == j - 1 \\ &d[j-1, j] + P_{(j-1)j} && \ if \ i == j\\ \end{align} \right.\]
- \(P_{ij}\) 表示点 \(i\) 到点 \(j\) 的距离
- 当 $i \neq j-1 $ 时,可以确保点 \(j-1\) 和 \(j\) 在一条路线上,可以直接使用递推式
- 当 \(i == j-1\) 时, \(j-1\) 和 \(j\) 不在同一条路线上,此时需要寻找连接点 \(j\) 的点,使整个巡游路线最短
- 为了避免重复计算,可以使用表 \(p[1..n, 1..n]\) 来储存 \(P[i, j]\) 的值,只需储存 \(i < j\) 的值即可
- 相关初始值:
-
\[d[1, 1] = 0, d[1, 2] = P_{12}, d[2, 2]=2P_{12} \]
-
-
-
\(d[n, n]\) 的值即为最短路径
-
为了重构两条路径,需要维护另外一张表,\(k[1..n, 1..n]\),其中 \(k[i, i+1], i = 1, \cdots, n\) 表示 \(i == j-1\) 时所选择的最优的点 \(u\)
- 点 \(n\) 为两条路径共有,设第一条路径拥有点 \(n-1\),则第二条路径拥有点 \(k[n-1, n]\), 而点 \(k[n-1, n] + 1 \cdots n-1\) 均在第一条路径中
- 先交换两边线路,然后再对点 \(k[(k[n-1, n]), (k[n-1, n] + 1)]\) 进行相同的操作
- \(k[1, 2]\) 的值需设为 \(1\)
%%writefile ch15/bitonic_eucliden_travel.py
"""思考题15-3 双调欧几里得旅行商问题"""
def bitonic_euclidean_travel(coordinates):
"""应确保 coordinates 的 x 坐标按升序排列"""
n = len(coordinates)
p = [[ ((coordinates[i][0] - coordinates[j][0]) ** 2 + (coordinates[i][1] - coordinates[j][1]) ** 2)**0.5 if i < j else 0
for j in range(n)]
for i in range(n)]
d = [[float('inf') if i == j-1 else 0
for j in range(n)]
for i in range(n)]
d[0][0] = 0
d[0][1] = p[0][1]
d[1][1] = 2 * p[0][1]
k = [[0]*n for i in range(n)]
k[0][1] = 1
for j in range(3, n+1):
for i in range(1, j+1):
if i == j - 1:
for u in range(1, j-1):
t = d[u-1][j-2] + p[u-1][j-1]
if t < d[i-1][j-1]:
d[i-1][j-1] = t
k[i-1][j-1] = u
elif i != j:
d[i-1][j-1] = d[i-1][j-2] + p[j-2][j-1]
else:
d[i-1][j-1] = d[j-2][j-1] + p[j-2][j-1]
# 重构解
first, second = [], []
i = n-1
while i > 1:
u = k[i-1][i]
first.extend(reversed(range(u+1, i+1)))
first, second = second, first
i = u
first = [coordinates[i-1] for i in first][::-1]
second = [coordinates[i-1] for i in second][::-1]
first.insert(0, coordinates[0])
second.insert(0, coordinates[0])
first.append(coordinates[-1])
second.append(coordinates[-1])
return d[-1][-1], first, second
if __name__ == "__main__":
coordinates = ((0, 6), (1, 0), (2, 3), (5, 4), (6, 1), (7, 5), (8, 2))
d, first, second = bitonic_euclidean_travel(coordinates)
print("最短的双调欧几里得路径为:", d, "第一条路径为:", first, "第二条路径为:", second)
Overwriting ch15/bitonic_eucliden_travel.py
!python ch15/bitonic_eucliden_travel.py
最短的双调欧几里得路径为: 25.58402459469133 第一条路径为: [(0, 6), (2, 3), (5, 4), (7, 5), (8, 2)] 第二条路径为: [(0, 6), (1, 0), (6, 1), (8, 2)]
15-4 整齐打印
问题分析
- 此问题的子问题为前 \(i(0\le i \le n)\) 个单词所占行的空格立方和的最大值 \(c[i]\)。原问题即为求解 \(c[n]\) 的最大值
- 可借助 \(c[1..j-1]\) 的值来求解 \(c[j](1 \le j \le n)\)
- 设 \(w_{ij} (1\le i \le j \le n)\) 为以 \(i\) 开头, \(j\) 结尾这些单词为一行所剩的空格数,对于给定的 \(j\), 设满足 \(w_{ij} \ge 0\) 的最小 \(i\) 值为 \(k\)
- 则可得:
-
\[c[j] = \left\{ \begin{align} \]
\end{align}\right.\[- 为了重构出最优解,需要另外一张表 $b[1..n]$,其中 $b[j]$ 用来储存上式取得最小值时的 $i$ \] -
%%writefile ch15/printing_neatly.py
"""思考题 15-4 整齐打印"""
def printing_neatly(X, M):
n = len(X)
c = [0] * (n+1)
b = [1] * n
for j in range(1, n+1):
c[j] = float('inf')
blanks = M + 1 # 补上 i == j 时所减去的空格
for i in reversed(range(1, j+1)):
blanks -= 1 + len(X[i-1])
if blanks < 0:
break
if j == n: # 最后一个元素,无需加上最后一行
if c[j-1] < c[j]:
b[j-1] = i
c[j] = c[j-1]
else:
t = c[i-1] + blanks ** 3
if t < c[j]:
b[j-1] = i
c[j] = t
# 重构最优解
last_word = [] # 储存每一行最后一个单词对应的下标
i = n
while i > 0:
last_word.append(i)
i = b[i-1] - 1
return c[n], last_word[::-1]
if __name__ == "__main__":
s = """
The Zen of Python, by Tim Peters
Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than right now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those1G!
""".split()
M = 80
cost, last_word = printing_neatly(s, M)
print("除最后一行外, 空格数立方的最小值之和为: ", cost)
print("最终的打印结果为: ")
print('*'*80)
for index, item in enumerate(last_word):
if index == 0:
print(" ".join(s[:item]).ljust(M, "|"))
else:
print(" ".join(s[last_word[index-1]:item]).ljust(M, "|"))
Overwriting ch15/printing_neatly.py
!python ch15/printing_neatly.py
除最后一行外, 空格数立方的最小值之和为: 1346
最终的打印结果为:
********************************************************************************
The Zen of Python, by Tim Peters Beautiful is better than ugly. Explicit||||||||
is better than implicit. Simple is better than complex. Complex is better|||||||
than complicated. Flat is better than nested. Sparse is better than dense.||||||
Readability counts. Special cases aren't special enough to break the rules.|||||
Although practicality beats purity. Errors should never pass silently. Unless|||
explicitly silenced. In the face of ambiguity, refuse the temptation to guess.||
There should be one-- and preferably only one --obvious way to do it. Although||
that way may not be obvious at first unless you're Dutch. Now is better than||||
never. Although never is often better than right now. If the implementation is||
hard to explain, it's a bad idea. If the implementation is easy to explain, it||
may be a good idea. Namespaces are one honking great idea -- let's do more of|||
those1G!||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
复杂度分析
- 程序总体有两个循环组成,因此时间复杂度为 \(O(n^2)\)
- 空间复杂度为 \(O(n)\)
15-5 编辑距离
a
算法分析
- 一对下标 \([i, j]\) 对应一个子问题, 设变换到下标 \(i, j\) ,总代价为 \(c[i, j]\)
- 目标是求解 \(c[m+1, n+1]\)
- 除终止处的其余5种操作的选用与 \([i, j]\) 的值和字符串 \(x\) 和 \(y\) 本身相关
- 复制
- 前提: \(x[i-1] == y[j-1]\)
- \(c[i, j] = c[i-1, j-1] + cost(copy)\)
- 替换
- 前提: \(x[i-1] \neq y[j-1]\)
- \(c[i,j] = c[i-1, j-1] + cost(replace)\)
- 删除
- 无前提
- \(c[i, j] = c[i-1, j] + cost(delete)\)
- 插入
- 无前提
- \(c[i, j] = c[i, j-1] + cost(insert)\)
- 交换
- 前提:\(x[i-1] = y[j-2], x[i-2] = j[i-1]\)
- \(c[i, j] = c[i-2, j-2] + cost(twiddle)\)
- 复制
- 如果 \(i\neq m+1\) 且 \(j \neq n+1\),\(c[i, j]\) 取上述 5 种操作的最小值(如果操作存在)即可
- 如果 \(i == m+1\) 且 \(j == n+1\),则需要考虑到终止操作,此时设上述 5 种操作的最小值为 \(min\_c\),则可得:
-
\[c[m+1, n+1] = min(min\_c, \min\limits_{1\le k \le m}{(c[k, n+1] + cost(kill))}) \]
-
- 序列值 \(c\) 为 \(c[1..m+1, 1..n+1]\),相关初始值如下
- \(c[1, 1] = 0\)
- \(c[1, j] = (j-1) * cost(insert), \ 1 \lt j \le n+1\)
- \(c[i, 1] = (i-1) * cost(delete), \ 1 \lt i \le m+1\)
- 重构最优解
- 为了重构最优解,需要另外一张表 \(d[1..m+1, 1..n+1]\), 其中 \(d[i,j]\) 用来记录变换到 \(c[i, j]\) 所执行的操作
- 相关初始值
- \(d[1, 1] = None\)
- \(d[1, j] = insert, 1 \lt j \le n+1\)
- \(d[i, 1] = delete, 1 \lt j \le n+1\)
- 重构最优解时,还要根据 \(c[m+1, n+1]\) 是否进行了 \(kill\) 操作进行特殊处理
代码实现
%%writefile ch15/edit_distance.py
"""思考题15-5 编辑距离"""
def edit_distance(x, y, cost):
"""求最小的编辑距离"""
m, n = len(x), len(y)
c = [[float('inf')]*(n+1) for i in range(m+1)]
d = [[None]*(n+1) for i in range(m+1)]
# 相关表项的初始化
c[0][0] = 0
for i in range(1, m+1):
c[i][0] = i * cost['delete']
d[i][0] = 'delete'
for j in range(1, n+1):
c[0][j] = j * cost['insert']
d[0][j] = 'insert'
for i in range(1, m+1):
for j in range(1, n+1):
if x[i-1] == y[j-1]: # copy
t = c[i-1][j-1] + cost['copy']
if t < c[i][j]:
c[i][j] = t
d[i][j] = 'copy'
else: # replace
t = c[i-1][j-1] + cost['replace']
if t < c[i][j]:
c[i][j] = t
d[i][j] = 'replace'
if i >= 2 and j >= 2 and x[i-1] == y[j-2] and x[i-2] == y[j-1]: # twiddle
t = c[i-2][j-2] + cost['twiddle']
if t < c[i][j]:
c[i][j] = t
d[i][j] = 'twiddle'
t = c[i-1][j] + cost['delete'] # delete
if t < c[i][j]:
c[i][j] = t
d[i][j] = 'delete'
t = c[i][j-1] + cost['insert'] # insert
if t < c[i][j]:
c[i][j] = t
d[i][j] = 'insert'
kill_index = -1
for k in range(0, m): # kill 操作
t = c[k][n] + cost['kill']
if t < c[m][n]:
kill_index = k + 1
c[m][n] = t
# 重构最优解
res = []
if kill_index == -1:
i, j = m, n
else:
i, j = kill_index, n
res.append('kill')
while i > 0 or j > 0:
if d[i][j] == 'copy':
res.append('copy {}'.format(x[i-1]))
i, j = i-1, j-1
elif d[i][j] == 'replace':
res.append('replace {} by {}'.format(x[i-1], y[j-1]))
i, j = i-1, j-1
elif d[i][j] == 'twiddle':
res.append('twiddle {} with {}'.format(x[i-1], x[i-2]))
i, j = i-2, j-2
elif d[i][j] == 'delete':
res.append('delete {}'.format(x[i-1]))
i = i - 1
elif d[i][j] == 'insert':
res.append('insert {}'.format(y[j-1]))
j = j -1
return c[m][n], res[::-1]
Writing ch15/edit_distance.py
import ch15.edit_distance
imp.reload(ch15.edit_distance)
from ch15.edit_distance import edit_distance
cost = dict(zip(('copy', 'replace', 'delete', 'insert', 'twiddle', 'kill'), (1, 4, 2, 3, 2, 1)))
x, y = 'algorithm', 'altruistic'
total_cost, res= edit_distance(x, y, cost)
print("编辑距离为:{}".format(total_cost), "操作过程为:", "\n".join(res), sep="\n")
编辑距离为:24
操作过程为:
copy a
copy l
delete g
replace o by t
copy r
insert u
insert i
insert s
twiddle t with i
replace h by c
kill
复杂度分析
- 时间复杂度和空间复杂度均为 \(O(mn)\)
b
-

-
最优化对齐的最终目的可以等效于修改两个 DNA 序列,以让它们相同。插入操作相当于在 \(x\) 中插入空格,删除操作相当于在 \(y\) 中插入空格。
-
由“打分”规则可知,复制操作的代价为 \(1\), 替换操作的代价为 \(-1\), 插入和删除的代价为 \(-2\),算法的目的相当于是寻找最大编辑距离
-
根据插入和删除操作,分别向 \(x\), 与 \(y\) 中插入空格,即可构造出最优解
%%writefile -a ch15/edit_distance.py
def align_sequences(x, y, cost):
"""借助编辑距离求序列对齐的最佳方案"""
m, n = len(x), len(y)
c = [[float('-inf')]*(n+1) for i in range(m+1)]
d = [[None]*(n+1) for i in range(m+1)]
# 相关表项的初始化
c[0][0] = 0
for i in range(1, m+1):
c[i][0] = i * cost['delete']
d[i][0] = 'delete'
for j in range(1, n+1):
c[0][j] = j * cost['insert']
d[0][j] = 'insert'
for i in range(1, m+1):
for j in range(1, n+1):
if x[i-1] == y[j-1]: # copy
t = c[i-1][j-1] + cost['copy']
if t > c[i][j]:
c[i][j] = t
d[i][j] = 'copy'
else: # replace
t = c[i-1][j-1] + cost['replace']
if t > c[i][j]:
c[i][j] = t
d[i][j] = 'replace'
t = c[i-1][j] + cost['delete'] # delete
if t > c[i][j]:
c[i][j] = t
d[i][j] = 'delete'
t = c[i][j-1] + cost['insert'] # insert
if t > c[i][j]:
c[i][j] = t
d[i][j] = 'insert'
# 重构最优解
i, j, x_blanks, y_blanks= m, n, [], []
while i > 0 or j > 0:
if d[i][j] == 'copy':
i, j = i-1, j-1
elif d[i][j] == 'replace':
i, j = i-1, j-1
elif d[i][j] == 'delete':
y_blanks.append(i-1)
i = i - 1
elif d[i][j] == 'insert':
x_blanks.append(j-1)
j = j -1
x_align, y_align = x, y
for item in x_blanks:
x_align = x_align[:item] + "*" + x_align[item:]
for item in y_blanks:
y_align = y_align[:item] + "*" + y_align[item:]
return c[m][n], x_align, y_align
Appending to ch15/edit_distance.py
import ch15.edit_distance
imp.reload(ch15.edit_distance)
from ch15.edit_distance import align_sequences
cost = dict(zip(('copy', 'replace', 'delete', 'insert'), (1, -1, -2, -2)))
x = "GATCGGCAT"
y = "CAATGTGAATC"
total_cost, x_align, y_align = align_sequences(x, y, cost)
print("最优对齐方案为:", x_align, y_align, sep="\n")
print("最优方案的分数为: ", total_cost)
最优对齐方案为:
*GATCGGCAT*
CAATGTGAATC
最优方案的分数为: -3
15-6 公司聚会计划
算法分析
- 为每个结点增加两个属性,分别是当前结点\(N\)参加时,以当前结点为根的子树(包含当前结点)的宾客最大交际分数 \(attend\_points\) 和当前结点不参加时,以当前结点为根的子树的宾客的最大交际分数 \(not\_attend\_points\)。问题的子问题就相当于求解属性 \(N.attend\_points\) 和 \(N.not\_attend\_points\)
- 设树根为 \(T\), 则原问题则相当于求解 \(\max \{T.attend\_points, T.not\_attend\_points\}\)
- 设结点 \(N\) 的子结点组成的集合为 \(S\), 则可得:
- \(N.attend\_points = \sum_{I \in S} I.not\_attend\_points\)
- \(N.not\_attend\_points = \sum_{I \in S} \max(I.not\_attend\_points, I.attend\_points)\)
- 构造最优解,可以通过遍历树,根据每个结点额外添加的两个属性以及当前结点的父结点是否能出席,来决定当前结点是否出席。为些需要在结点中添加 \(attend\) 属性来判断当前人员是否出席
代码实现
%%writefile ch15/party_plan.py
from collections import deque
class Node():
"""用来储存职员信息的结点"""
def __init__(self, name=None, left_child=None, right_sibling=None, parent=None, point=0):
self.name = name
self.left_child = left_child
self.right_sibling = right_sibling
self.point = point
self.parent = parent
self.attend = None
self.attend_points = None
self.not_attend_points = None
def __repr__(self):
return str(self.name)
def calc_points(root):
"""计算特定结点的 attend_points 和 not_attend_points 属性"""
if root.attend_points is not None: # 避免重复计算
return
root.attend_points = root.point
root.not_attend_points = 0
child = root.left_child
while child is not None:
calc_points(child)
root.attend_points += child.not_attend_points
root.not_attend_points += max(child.attend_points, child.not_attend_points)
child = child.right_sibling
def party_plan(root):
"""思考题 15-6 公司聚会计划"""
calc_points(root) # 自顶向下计算 attend_points 和 not_attend_points 属性
# 层级遍历,构造出席人员
res = []
if root.attend_points > root.not_attend_points:
root.attend, max_points = True, root.attend_points
res.append(root)
else:
root.attend, max_points = False, root.not_attend_points
if root.left_child is None:
return max_points, res
dq = deque()
dq.append(root.left_child)
while len(dq) > 0:
x = dq.popleft()
y = x
while y is not None:
if y.left_child is not None:
dq.append(y.left_child)
if y.parent.attend or y.attend_points < y.not_attend_points:
y.attend = False
else:
y.attend = True
res.append(y)
y = y.right_sibling
return max_points, res
Writing ch15/party_plan.py
import ch15.party_plan
imp.reload(ch15.party_plan)
from ch15.party_plan import Node, party_plan
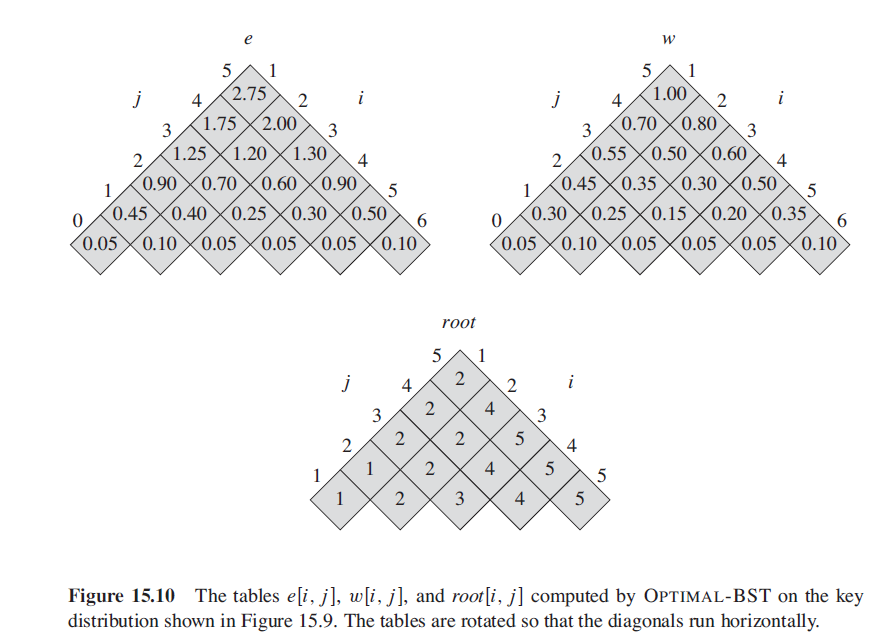
- 构造结点按此图进行, 分数随机生成
-
points = [random.randint(1, 100) for i in range(14)]
N01 = Node(name='N01', point=points[0])
N11 = Node(name='N11', point=points[1])
N12 = Node(name='N12', point=points[2])
N13 = Node(name='N13', point=points[3])
N21 = Node(name='N21', point=points[4])
N22 = Node(name='N22', point=points[5])
N23 = Node(name='N23', point=points[6])
N24 = Node(name='N24', point=points[7])
N25 = Node(name='N25', point=points[8])
N26 = Node(name='N26', point=points[9])
N27 = Node(name='N27', point=points[10])
N31 = Node(name='N31', point=points[11])
N32 = Node(name='N32', point=points[12])
N33 = Node(name='N33', point=points[13])
N01.left_child = N11
N11.parent = N01
N12.parent = N01
N13.parent = N01
N11.right_sibling = N12
N12.right_sibling = N13
N11.left_child = N21
N12.left_child = N23
N13.left_child = N27
N21.parent = N11
N22.parent = N11
N21.right_sibling = N22
N22.left_child = N31
N23.parent = N12
N24.parent = N12
N25.parent = N12
N26.parent = N12
N23.right_sibling = N24
N24.right_sibling = N25
N25.right_sibling = N26
N25.left_child = N32
N27.parent = N13
N31.parent = N22
N32.parent = N25
N33.parent = N25
N32.right_sibling = N33
points
[38, 84, 11, 3, 14, 9, 86, 95, 34, 19, 46, 13, 82, 20]
max_points, res = party_plan(N01)
print("最高交际分数为:", max_points)
print("出席的人员为: ", ', '.join([str(item) for item in res]))
最高交际分数为: 445
出席的人员为: N11, N23, N24, N26, N27, N31, N32, N33
复杂度分析
- 算法对树中的每个元素都遍历的常数次,而且对每个结点额外添加了 3 个属性,因此时间和空间复杂度均为 \(O(n)\)
15-7 译码算法
-

-
与图算法相关,看完图的相关内容后再补
15-8 基于接缝裁剪的图像压缩
a
- 当 \(n>1\) 时,每次至少有 \(2\) 种选择,如果其上一行选择的点不在边界,则至少有 \(3\) 种选择, \(m\) 行至少有 \(2^m\) 种选择,为 \(m\) 的指数函数
b
算法分析
- 设 \(c[i, j]\) 表示 \([i, j]\) 点被删除后,前 \(i\) 行(包括第 \(i\) 行)的最低破坏度之和,则原问题的解为:
- \(\min\limits_{1\le k \le n}{c[m, k]}\)
- 子问题 \(c[i, j]\) 的解为:
- \(c[i, j] = \left\{ \begin{align} &\min(c[i-1, j], c[i, j+1]) + d[i, j] && i \neq 1 \ and\ j = 1 \\ &\min(c[i-1, j-1], c[i-1, j], c[i-1, j+1]) + d[i, j] && i \neq 1 \ and \ 1 \lt j \lt n\\ &\min(c[i-1, j-1], c[i-1, j]) + d[i, j] && i \neq 1 \ and\ j = n \\ &d[i, j] && i = 1 \\ \end{align} \right.\)
- 构造最优解根据序列\(c[1..m, 1..n]\) 的值即可求出
代码实现
%%writefile ch15/seam_carving.py
def seam_carving(d):
"""思考题 15-8: 基于接链裁剪的图像压缩"""
m, n = len(d), len(d[0])
c = [[d[i][j] if i == 0 else 0 for j in range(n)] for i in range(m)]
for i in range(1, m):
c[i][0] = min(c[i-1][0], c[i-1][1]) + d[i][0]
for j in range(1, n-1):
c[i][j] = min(c[i-1][j-1], c[i-1][j] ,c[i-1][j+1]) + d[i][j]
c[i][n-1] = min(c[i-1][n-2], c[i-1][n-1]) + d[i][j]
# 重构最优解
mini_cost, k = float('inf'), None
for i, item in enumerate(c[m-1]):
if item < mini_cost:
mini_cost, k = item, i
res = [None] * m
i = m - 1
res[i] = (m, k+1) # 储存剪切的位置
for j in reversed(range(m-1)):
mini_index = k
if k != 0 and c[j][k-1] < c[j][mini_index]:
mini_index = k - 1
if k != n-1 and c[j][k+1] < c[j][mini_index]:
mini_index = k + 1
i -= 1
res[i] = ((j+1, mini_index+1))
k = mini_index
return mini_cost, res
if __name__ == "__main__":
import random
d = [[random.randint(10, 99) for j in range(8)] for i in range(6)]
print("破坏度矩阵为:")
print("\n".join([str(item) for item in d]))
mini_cost, res = seam_carving(d)
print("最小破环度为: ", mini_cost)
print("裁剪位置为:", res)
res_sum = sum(d[item[0]-1][item[1]-1] for item in res)
assert res_sum == mini_cost
Overwriting ch15/seam_carving.py
!python ch15/seam_carving.py
破坏度矩阵为:
[70, 67, 87, 57, 68, 74, 97, 81]
[41, 12, 74, 31, 21, 33, 44, 35]
[39, 26, 33, 13, 10, 33, 88, 44]
[17, 24, 40, 94, 38, 61, 33, 74]
[77, 99, 38, 75, 54, 44, 70, 24]
[59, 47, 68, 76, 86, 87, 62, 74]
最小破环度为: 214
裁剪位置为: [(1, 2), (2, 2), (3, 2), (4, 2), (5, 3), (6, 2)]
复杂度分析
- 有内外两个循环,时间复杂度为 \(\Theta(mn)\)
15-9 字符串拆分
算法分析
- 此问题与矩阵链乘法基本相同,可以先从 \(L\) 中随机选择一个拆分点,此操作下的最小代价等于其左边子字符串操作的最小代价加上其右边子字符串操作的最小代价,符合最优子结构的相关特征
- 为了便于分析问题,扩充数组 \(L\),在其左右分别加入 \(1, n\),如此数组 \(L\) 变为 \(L[0..m+1]\),且 \(L[0]=1, L[m+1]=n\)
- 定义 \(c[i, j](i \lt j)\) 表示将 \(s[L[i], L[j])\) 中的元素按数组 \(L\) 划分的最小拆分代价,则原问题相当于求解 \(c[0, m+1]\)
- \(c[i, j]\) 可按以下公式计算得到:
-
\[c[i, j] =\left \{ \begin{align} \]
&\min\limits_{i\lt k \lt j}{(c[i, k] + c[k, j] - 1 + (L[j] - L[i] + 1))} && \ if \ i < j - 2 \
\end{align}\right.$$- \(c[i, i+1]\) 设置为 \(1\) 的目的是方便 $i < j - 2 $ 时的计算
-
- 定义 \(d[i, j](i < j -2 )\) 为 \(c[i, j]\) 取得最小值时的 \(k\),以此可重构出最优拆分序列
- 当 \(j=i+2\) 时,有 \(d[i][j] = i + 1\)
代码实现
%%writefile ch15/string_break.py
def string_break(n, L):
"""思考题 15-9 字符串拆分"""
m = len(L)
L = [1] + list(L) + [n]
c = [[L[j]-L[i] + 1 if j == i+2 else 1
for j in range(m+2)]
for i in range(m+2)]
d = [[i+1 if j == i+2 else None
for j in range(m+2)]
for i in range(m+2)]
for l in range(4, m+3):
for i in range(0, m+3-l):
j = i + l - 1
c[i][j] = float('inf')
for k in range(i+1, j):
t = c[i][k] + c[k][j] + L[j] - L[i]
if t < c[i][j]:
c[i][j] = t
d[i][j] = k
mini_cost = c[0][m+1] # 最小代价
res = []
construct_break_sequence(L, d, m, res, 0, m+1)
return mini_cost, res
def construct_break_sequence(L, d, m, res, i, j):
"""构造最优拆分序列"""
k = d[i][j]
res.append(L[k])
if k > i + 1:
construct_break_sequence(L, d, m, res, i, k)
if k < j - 1:
construct_break_sequence(L, d, m, res, k, j)
if __name__ == "__main__":
n = 20
L = [2, 8, 10]
mini_cost, res = string_break(n, L)
print("最小拆分代价为:", mini_cost)
print("对应的拆分序列为:", res)
Overwriting ch15/string_break.py
!python ch15/string_break.py
最小拆分代价为: 38
对应的拆分序列为: [10, 8, 2]
15-10
a
- 10 年的最优投资策略,可看做由几个分开的不转移资产的连续年份组成
- 假设第 \(j_1\) 至 \(j_2\) 年不转移资产, 则应选择 \(\sum_{j=j_1}^{j_2}{r_{ij}}\) 最高的产品进行投资才能获得最高的收益
- 因此,存在最优投资策略,每年都将所有钱放入到单一投资中
b
- 设 \(c[i, j]\) 表示第 \(j\) 年选择第 \(i\) 种投资的最大收益
- 如果第 \(j\) 年没有切换投资项目,则
- \(c[i, j] = (c[i, j-1] - f_1) * r_{ij}\)
- 如果第 \(j\) 年切换了投资项目
- \(c[i, j] = (\max\limits_{1\le k \le n, \ k\neq i}\{c[k, j-1]\} - f_2) * r_{ij}\)
- \(c[i, j]\) 取为 \(1, 2\) 中结果的最大值
- 第 \(j\) 年投资 \(i\) 的收益只与第 \(j-1\) 年的收益相关,因此具有最优子结构的特征
c
- 末来 \(n\) 年的最大化投资收益等于 \(\max\limits_{1\le k \le n}c[k, n]\)
- 需要另外一个序列 \(d[1..n, 1..n]\) 来储存获得 \(c[i, j](i > 2)\) 时的前一年投资的项目,以便重构最优解
代码实现
%%writefile ch15/invest_strategy.py
"""练习题 15-10: 投资策略规划"""
def invest_strategy(R, money, f1, f2):
"""R 储存了 n 种投资 m 年的收益"""
n, m = len(R), len(R[0])
c = [[money * R[i][0] if j == 0 else float('-inf')
for j in range(m)]
for i in range(n)]
d = [[None]* (m) for i in range(n)]
for j in range(1, m):
for i in range(n):
for k in range(n):
if i == k:
t = (c[k][j-1] - f1) * R[i][j]
else:
t = (c[k][j-1] - f2) * R[i][j]
if t > c[i][j]:
c[i][j] = t
d[i][j] = k
max_profit, k = float('-inf'), None
for i in range(n):
if c[i][m-1] > max_profit:
max_profit, k = c[i][m-1], i
res = [None] * m
res[-1] = k + 1
for i in reversed(range(m-1)):
res[i] = d[res[i+1] - 1][i+1] + 1
return max_profit, res
if __name__ == "__main__":
import numpy as np
n, m = 5, 10
R = np.random.random((n, m)) / 8 + 1
money = 10 ** 4
f1 = 50
f2 = 500
max_profit, res = invest_strategy(R, money, f1, f2)
print("共有 {} 种投资, 投资年限为 {} 年".format(n, m))
np.set_printoptions(precision=3, suppress=True, linewidth=100)
print("每种投资的回报率为: \n", str(R))
print("本金为: ", money)
print("f1 = {}, f2 = {}".format(f1, f2))
print("*"*50)
print("最大收益为: ", max_profit)
print("投资顺序为:", res)
Overwriting ch15/invest_strategy.py
!python ch15/invest_strategy.py
共有 5 种投资, 投资年限为 10 年
每种投资的回报率为:
[[1.018 1.079 1.061 1.066 1.045 1.015 1.026 1.044 1.081 1.008]
[1.04 1.087 1.068 1.041 1.053 1.09 1.105 1.089 1.102 1.014]
[1.115 1.024 1.072 1.024 1.027 1.049 1.024 1.119 1.04 1.06 ]
[1.052 1.072 1.025 1.093 1.032 1.11 1.032 1.067 1.045 1.042]
[1.108 1.024 1.002 1.083 1.049 1.111 1.091 1.109 1.077 1.121]]
本金为: 10000
f1 = 50, f2 = 500
**************************************************
最大收益为: 21343.92608956265
投资顺序为: [3, 2, 2, 5, 5, 5, 5, 5, 5, 5]
时间复杂度
- 算法中共有 \(3\) 个循环,时间复杂度为 \(O(mn^2)\)
d
- 经过 \(n\) 年的投资,总金额可能大于 15000 美元,此时会影响到后续的投资策略,不能再全部投入一类产品。此时问题不能再通过其子问题求出,因此不再具有最优子结构。
15-11 库存规划
算法分析
- 此问题有以下隐藏条件
- \(n\) 个月的总生产数量不能超过 \(D\) 台
- 为了满足第 \(i(i \gt 1)\) 个月销售, 第 \(i\) 个月的生产数量应大于等于 \((d_{i}\ -\ 第\ i-1 \ 月的库存量)\)
- 第 \(i(i>1)\) 月的成本以及生产计划需要视上个月的库存而定,而本月的库存又会影响到下一个月的库存和生产计划
- 因此选用 \(c[i, j]\) 表示第 \(i\) 个月的库存为 \(j\) 的成本, \(c\) 的序列为 \(c[1..n, 1..D]\),
- 选定序列 \(w[0..n]\) 表示前 \(i\) 个月的总销售量,即 \(w[i] = \sum_{k=0}^{i}{d_k}\),设 \(w[0] = 0, d_0 = 0\)
- 则第 \(i\) 个月的库存量至多为 $ D-w[i]$,则 \(c[i, j]\) 需要满足 \(j \le D-w[i]\)
- 为了使得第 \(i\) 个月后库存为 \(j\),则第 \(i-1\) 个月的库存不能超过 \(j+d_i\)
- 可得 \(i>1\) 时 \(c[i, j]\) 的计算公式如下:
- \(c[i, j] = \min\limits_{0 \le k \le \min(D-w[i-1], j+d_i)}\{{c[i-1, k] + p(j-k+d_i) + h(j)}\}\)
- \(p(x)\) 为生产成本,即
- \(p(x) = \left\{ \begin{align} &0 && if \ x \le m \\ &c(x-m) && if \ x \gt m \end{align}\right.\)
- \(h(x)\) 为储存成本,设 \(h(0) = 0\)
- \(p(x)\) 为生产成本,即
- 令 \(b[i, j] = k\), 即用来储存 \(c[i, j]\) 取得最小值时上一个月的仓库储量 \(k\)
- 已知 \(k, j\) 后借助 \(f(j-k+d_i)\) 即可算出当前月的生产量,以此便可重构最优的生产序列
- \(c[i, j] = \min\limits_{0 \le k \le \min(D-w[i-1], j+d_i)}\{{c[i-1, k] + p(j-k+d_i) + h(j)}\}\)
- 原问题相当于求解\(c[n, 0]\)
代码实现
%%writefile ch15/invest_strategy.py
"""思考题 15-11 库存规划"""
def invertory_plan(d):
"""库存规划
"""
n, D = len(d), sum(d)
c = [[ 0 if i == 0 else float('inf')
for j in range(D+1)]
for i in range(n+1)]
b = [[0]*(D+1) for i in range(n+1)]
w = [0]*(n+1)
for i in range(1, n+1):
w[i] = w[i-1] + d[i-1]
for j in range(D-w[i]+1):
c[i][j] = c[i-1][0] + product_cost(j+d[i-1]) + invertory_cost(j)
if i == 1:
continue
for k in range(min(D-w[i-1], j+d[i-1])):
t = c[i-1][k] + product_cost(j-k+d[i-1]) + invertory_cost(j)
if t < c[i][j]:
c[i][j] = t
b[i][j] = k
# 重构最优生产序列
res, k = [0] * n, b[n][0]
res[n-1] = -k+d[n-1]
for i in reversed(range(i-1)):
t = b[i+1][k]
res[i] = k-t+d[i]
k = t
return c[n][0], res
def product_cost(x, m=10, c=1000):
"""生产成本`"""
return 0 if x <=m else (x-m) * c
def invertory_cost(x):
"""存储成本"""
return 250 * x
if __name__ == "__main__":
import random
d = [random.randint(0, 20) for i in range(11)] + [0]
m, c = 10, 1000
cost, res= invertory_plan(d)
print("m = {}, c = {}".format(m, c))
print("每件的储存成本为: 250")
print("每个月销售量为:", d)
print("*"*60)
print("每个月的最优生产序列为: ", res)
print("最低成本为: ", cost)
Overwriting ch15/invest_strategy.py
!python ch15/invest_strategy.py
m = 10, c = 1000
每件的储存成本为: 250
每个月销售量为: [10, 13, 3, 13, 10, 16, 14, 0, 19, 9, 3, 0]
************************************************************
每个月的最优生产序列为: [10, 13, 10, 10, 10, 12, 14, 9, 10, 9, 3, 0]
最低成本为: 15000
复杂度分析
- 算法共有三层循环,运行的时间复杂度为 \(O(nD^2)\)
15-12 签约棒球自由球员
算法分析
- 此问题有两个变量,一是球员的位置,还有一个是签约的总费用,目的是为了使得总的 \(VORP\) 值最大
- 设 \(c[i, j]\) 表示签约费用为 \(j\) 时,签约 \(i\) 个不同位置的球员的的最大 \(VORP\) 值,则原问题相当于求解 \(c[N, X]\), \(c[N, X]\) 可由其子问题的最优解构成
- \(i \gt 1\) 时,\(c[i, j]\) 的求解可分为两种情况
- 在位置 \(i\) 处不签入球员
- \(c_1= c[i-1, j]\)
- 在位置 \(i\) 处签入球员
- 设位置 \(i\) 处的球员集合为 \(player\)
- \(c_2= \max\limits_{1\le k \le P}\{{c[i-1, j-player_k.cost] + player_k.VORP\}}\)
- 如果对于某个 \(k\),有 \(j-player_k.cost \lt 0\),则该 \(k\) 不计入考虑
- \(c[i, j] = \max(c_1, c_2)\)
- 为了重构最优解,需要用 \(d[i, j]\) 来记录 \(c[i, j]\) 取得最优值时所签入的球员编号 \(k\) 如果没有签入球员,则 \(k=0\)
- 假设每位球员的签约费用为 10 万美元的整数倍,则 \(j\) 的最大值可取为 \(x = \lfloor X / 10^5\rfloor\)
- 为了简化算法,设 \(c\) 对应的序列为 \(c[0..N, 0..x]\), 其中 \(c[0, j] = c[i, 0] = 0\)
代码实现
%%writefile ch15/signing_players.py
"""思考题 15-2: 签约棒球自由球员"""
from collections import namedtuple
Player = namedtuple('Player', 'index, cost, VORP') # 球员属性, cost 的单位为十万
def signing_players(M, X):
"""M 应有 n 行 p 列,分别对应 N 个位置,以及每个位置上有 P 个可选球员"""
N, P = len(M), len(M[0])
x = X // 10 ** 5
c = [[0]*(x+1) for i in range(N+1)]
d = [[0]*(x+1) for i in range(N+1)]
for i in range(1, N+1):
for j in range(1, x+1):
c[i][j] = float('-inf')
if c[i-1][j] > c[i][j]:
c[i][j], d[i][j] = c[i-1][j], 0
for k in range(P):
remain_money = j - M[i-1][k].cost
if remain_money < 0:
continue
t = c[i-1][remain_money] + M[i-1][k].VORP
if t > c[i][j]:
c[i][j], d[i][j] = t, k+1
# 重构最优解
i, j, res = N, x, []
while i > 0 and j > 0:
k = d[i][j]
if k != 0:
res.append(M[i-1][k-1])
i ,j = i-1, j - res[-1].cost
else:
i -= 1
return c[N][x], res[::-1]
if __name__ == "__main__":
import random
N, P = 9, 6
M = [[Player("{}{}".format(i+1, j+1), random.randint(1, 9), random.randint(60, 99))
for j in range(P)]
for i in range(N)]
X = 12 * 10 ** 5
print("球员信息为: \n")
print("\n".join(str(item) for item in M))
print("总的招聘费用为:{:.2f} 十万".format(X/10**5))
print("*"*50)
cost, res = signing_players(M, 12 * 10 ** 5)
print("招入的球员为: ")
print("\n".join(str(item) for item in res))
print("最大 VORP 值为:", cost)
Overwriting ch15/signing_players.py
!python ch15/signing_players.py
球员信息为:
[Player(index='11', cost=5, VORP=62), Player(index='12', cost=9, VORP=75), Player(index='13', cost=8, VORP=83), Player(index='14', cost=3, VORP=91), Player(index='15', cost=2, VORP=86), Player(index='16', cost=6, VORP=74)]
[Player(index='21', cost=7, VORP=77), Player(index='22', cost=1, VORP=72), Player(index='23', cost=3, VORP=60), Player(index='24', cost=4, VORP=69), Player(index='25', cost=5, VORP=62), Player(index='26', cost=8, VORP=95)]
[Player(index='31', cost=6, VORP=78), Player(index='32', cost=8, VORP=83), Player(index='33', cost=8, VORP=93), Player(index='34', cost=7, VORP=62), Player(index='35', cost=7, VORP=97), Player(index='36', cost=2, VORP=80)]
[Player(index='41', cost=6, VORP=66), Player(index='42', cost=2, VORP=87), Player(index='43', cost=3, VORP=75), Player(index='44', cost=9, VORP=66), Player(index='45', cost=4, VORP=81), Player(index='46', cost=3, VORP=72)]
[Player(index='51', cost=9, VORP=75), Player(index='52', cost=3, VORP=60), Player(index='53', cost=1, VORP=66), Player(index='54', cost=3, VORP=73), Player(index='55', cost=2, VORP=82), Player(index='56', cost=3, VORP=95)]
[Player(index='61', cost=3, VORP=67), Player(index='62', cost=3, VORP=83), Player(index='63', cost=8, VORP=73), Player(index='64', cost=2, VORP=93), Player(index='65', cost=6, VORP=88), Player(index='66', cost=8, VORP=96)]
[Player(index='71', cost=6, VORP=70), Player(index='72', cost=2, VORP=88), Player(index='73', cost=7, VORP=70), Player(index='74', cost=4, VORP=85), Player(index='75', cost=4, VORP=97), Player(index='76', cost=3, VORP=66)]
[Player(index='81', cost=2, VORP=87), Player(index='82', cost=6, VORP=81), Player(index='83', cost=5, VORP=67), Player(index='84', cost=8, VORP=86), Player(index='85', cost=2, VORP=74), Player(index='86', cost=4, VORP=96)]
[Player(index='91', cost=5, VORP=95), Player(index='92', cost=3, VORP=68), Player(index='93', cost=9, VORP=79), Player(index='94', cost=4, VORP=86), Player(index='95', cost=4, VORP=74), Player(index='96', cost=6, VORP=96)]
总的招聘费用为:12.00 十万
**************************************************
招入的球员为:
Player(index='15', cost=2, VORP=86)
Player(index='22', cost=1, VORP=72)
Player(index='42', cost=2, VORP=87)
Player(index='53', cost=1, VORP=66)
Player(index='64', cost=2, VORP=93)
Player(index='72', cost=2, VORP=88)
Player(index='81', cost=2, VORP=87)
最大 VORP 值为: 579
复杂度分析
- 令 \(x = \lfloor X / 100000\rfloor\)
- 算法的时间复杂度为 \(O(NxP)\)
- 空间复杂度为 \(O(NP)\)