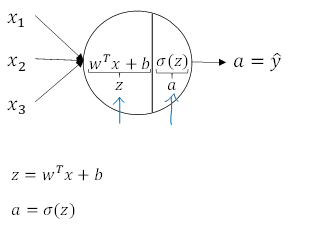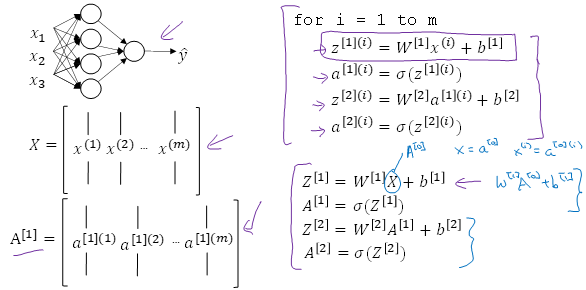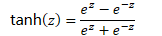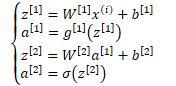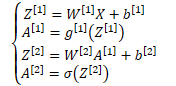吴恩达deeplearning.ai -- week3 浅层神经网络
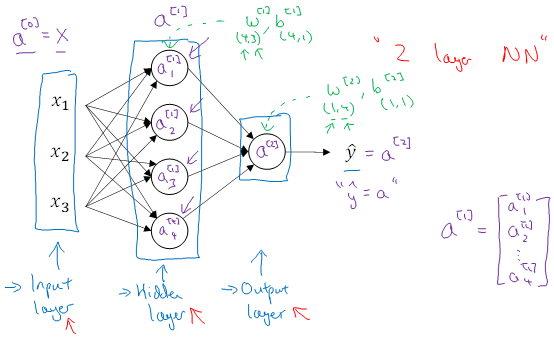
- 双层神经网络基础
- 基本特点
- 单个节点包含线性函数和激活函数
- 符号含义
- 指示相关变量所对应的节点和层数
- 神经网络的表示方法
- 矩阵表示
- 激活函数的选取

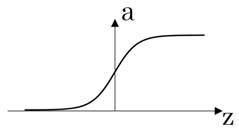
- Sigmod 函数
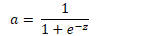
- 一般在二分分类中用作输出层
- tanh 函数
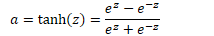
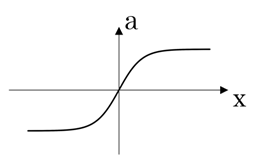
- 值在 -1 到 1 之间
- 效果普遍要优于 Sigmod 函数,但 x 较大或较小时,斜率接近于 0,梯度下降法收敛较慢
- ReLu函数

- z 为负时,导数为 0
- 特点
- 应用较多,收敛速度较多
- z 为负时,导数为0,但是实际应用时,一般有足够多的隐藏单元格使得 z > 0
- Leaky ReLu
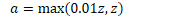
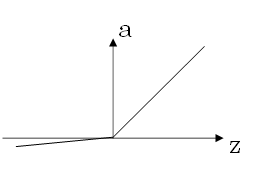
- z 为负时,导数不再为 0
- 效果一般要比 ReLu 函数好,但实际中较少使用
- 为什么隐藏层需要非线性的激活函数
- 如果使得线性的激活函数,那么神经网络只是把输入线性组合再输出。如此输入与输出之间也只是线性关系,隐藏层基本上没有作用
- 常用激活函数的导数
原函数 | 导数 |
|
|
|
|
- 梯度下降法
- logistic 回归
- 由向量求导的运算,借助矩阵乘法的性质,推广到矩阵运算
正向求解过程 | 反向求导数过程 | ||||||||
|
|
- 参数 b 在 numpy 中会通过广播的形式参与运算
- numpy 广播的规则
- 让所有输入数组都向其中形状最长的数组看齐,形状中不足的部分都通过在前面加 1 补齐。
- 输出数组的形状是输入数组形状的各个维度上的最大值。
- 如果输入数组的某个维度和输出数组的对应维度的长度相同或者其长度为 1 时,这个数组能够用来计算,否则出错。
当输入数组的某个维度的长度为 1 时,沿着此维度运算时都用此维度上的第一组值。
- * 在 numpy 中为按元素相乘
- 反向求导的矩阵运算中,变量的求导为对损失函数求导,参数的求导为对成本函数求导

- 两个矩阵相乘的结果,等于左矩阵的行向量,对应乘以右矩阵的列向量的结果和(可以通过矩阵乘法的定义证明)
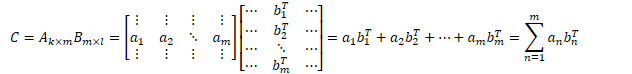
- 矩阵乘法的定义
- 初始值的选取
- 如果将参数 W 全部初始化为0,则无论经过多少次迭代,W 中的元素仍然相同,如此会使得隐藏层的存在失去意义
- 一般 W 会选择随机初始化
np.random.randn(2,2) * 0.01 |
- 所乘的系数选为 0.01,其不宜过大;如过大,则对于 sigmod 或 tanh 函数来说,初始收敛过慢