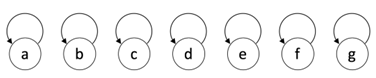14 并查集

• 基本概念
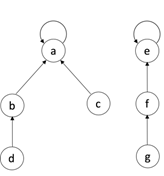
  • 并查集是一种树型的数据结构，用于处理一些不交集的合并及查询问题
  • 示意图
    • 
• 常用方法
  • Find：确定元素属于哪一个子集。可以用来确定两个元素是否属于同一子集
  • Union： 将两个子集合并成同一个集合
  • 示意图
    • 
    • 
• 代码实现（伪代码）

function MakeSet(x)

    x.parent := x

    

function Find(x)

    if x.parent == x

        return x

    else

        return Find(x.parent)

        

function Union(x, y)

    xRoot := Find(x)

    yRoot := Find(y)

    xRoot.parent := yRoot

  

• 优化
  • rank
    • 示意图
      • 
    • 伪代码

function MakeSet(x)

    x.parent := x

    x.rank := 0

        

function Union(x, y)

    xRoot := Find(x)

    yRoot := Find(y)

    if xRoot == yRoot

        return

        

    if xRoot.rank < yRoot.rank

        xRoot.parent := yRoot

    else if xRoot.rank > yRoot.rank

        yRoot.parent := xRoot

    else

        yRoot.parent := xRoot

        xRoot.rank := xRoot.rank + 1

   

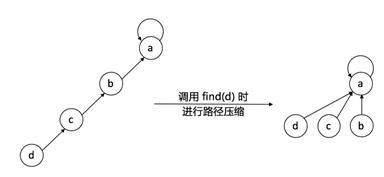
• 路径压缩
  • 示意图
    • 
  • 伪代码

function MakeSet(x)

    x.parent := x

    

function Find(x)

    root = x

    while root != root.parent

        root := root.parent

    

    while x != x.parent

        tmp = x.parent

        x.parent = root

        x = tmp

        

    return root

   

• Python 实现 -- 包含两种优化

class UnionUF(object):

    def __init__(self, n):

        self.parent = [-1] * n

        self.rank = [0] * n

        for i in range(n):

            self.parent[i] = i

   

    def find(self, i):

        root = i

        while root != self.parent[root]:

            root = self.parent[root]

   

        # 路径压缩

        while i != self.parent[i]:

            i, self.parent[i] = self.parent[i], root

   

        return root

   

    def union(self, x, y):

        rootx = self.find(x)

        rooty = self.find(y)

        if rootx == rooty:

            return 0# 两者属于同一集合,没有发生合并操作

        if self.rank[rootx] > self.rank[rooty]:

            self.parent[rooty] = rootx

        elif self.rank[rootx] < self.rank[rooty]:

            self.parent[rootx] = rooty

        else:

            self.parent[rootx] = rooty

            self.rank[rooty] += 1

        return 1# 发生合并操作 

• letcode 例题
  • https://leetcode.com/problems/number-of-islands/

class UnionUF(object):

    def __init__(self, n):

        self.parent = [-1] * n

        self.rank = [0] * n

        for i in range(n):

            self.parent[i] = i

   

    def find(self, i):

        root = i

        while root != self.parent[root]:

            root = self.parent[root]

   

        # 路径压缩

        while i != self.parent[i]:

            i, self.parent[i] = self.parent[i], root

   

        return root

   

    def union(self, x, y):

        rootx = self.find(x)

        rooty = self.find(y)

        if rootx == rooty:

            return 0# 两者属于同一集合,没有发生合并操作

        if self.rank[rootx] > self.rank[rooty]:

            self.parent[rooty] = rootx

        elif self.rank[rootx] < self.rank[rooty]:

            self.parent[rootx] = rooty

        else:

            self.parent[rootx] = rooty

            self.rank[rooty] += 1

        return 1# 发生合并操作

            

            

class Solution:

    def numIslands(self, grid: List[List[str]]) -> int:

        if not grid:

            return 0

        m, n = len(grid), len(grid[0])

        union = UnionUF(m*n)

        res = 0

        dx, dy = [-1, 1, 0, 0], [0, 0, -1, 1]

        

        for i in range(m):

            for j in range(n):

                if grid[i][j] == "1":

                    res += 1

                    for count in range(len(dx)):

                        ni, nj = i + dx[count], j + dy[count]

                        if 0 <= ni < m and 0 <= nj < n and grid[ni][nj] == "1":

                            res -= union.union(i*n + j, ni*n + nj)

        return res

   

• https://leetcode.com/problems/friend-circles/submissions/

class UnionUF(object):

    def __init__(self, n):

        self.parent = [-1] * n

        self.rank = [0] * n

        for i in range(n):

            self.parent[i] = i

   

    def find(self, i):

        root = i

        while root != self.parent[root]:

            root = self.parent[root]

   

        # 路径压缩

        while i != self.parent[i]:

            i, self.parent[i] = self.parent[i], root

   

        return root

   

    def union(self, x, y):

        rootx = self.find(x)

        rooty = self.find(y)

        if rootx == rooty:

            return 0# 两者属于同一集合,没有发生合并操作

        if self.rank[rootx] > self.rank[rooty]:

            self.parent[rooty] = rootx

        elif self.rank[rootx] < self.rank[rooty]:

            self.parent[rootx] = rooty

        else:

            self.parent[rootx] = rooty

            self.rank[rooty] += 1

        return 1# 发生合并操作

   

   

class Solution:

    def findCircleNum(self, M: List[List[int]]) -> int:

        if not M:

            return 0

        m = len(M)

        union = UnionUF(m)

        res = 0

   

        for i in range(m):

            res += 1

            for count in range(m):

                if i == count:

                    continue

                if M[i][count] == 1:

                    res -= union.union(i, count)

        return res