计算离散点的边界 MATLAB计算多维凸包
无论是进行回归、拟合还是深度学习,总要将总体数据集划分为训练样本集和测试样本集。然而,一般情况下,测试集位于训练集“所覆盖的范围之内”时(如下图所示,红色星号表示训练样本集所在位置,蓝色圆点表示测试样本集所在位置),测试效果较好,测试结果也更具合理性。但是如何验证测试集是否在训练集“所覆盖的范围之内”呢?

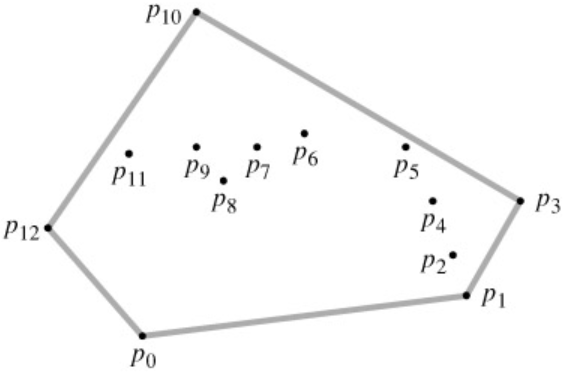
如下图所示,明显的,P0、P1和P3位于数据集的边界上,这些在边界上的点有什么特征呢?像是用一根橡皮筋套住所有这些点所形成的图案,该过程在数学上被定义为二维凸包(点集Q的凸包(convex hull)是指一个最小凸多边形,满足Q中的点或者在多边形边上或者在其内)。所以,如果能够根据样本数据集计算出样本数据集的凸包,就能标记出样本数据集中哪些数据点位于数据集的边界,进一步的,筛选测试样本集时避开这些边界点即可。一般情况下训练和测试样本的维度较高,所以可以通过计算多维凸包的方式来进行判断。
Matlab计算多维凸包的函数为 convhull (支持二维和三维)和 convhulln (支持$N$维,$N\ge 2$),以计算点集的凸包为例:
K = convhull(x,y)
其中,x 和 y 分别为点集的横纵坐标,K表示绕凸包沿逆时针方向排列的点的索引。
计算案例如下:
clear,clc
%% 计算二维随机点的凸包
x=normrnd(0,1,1,50);
y=normrnd(0,1,1,50);
K = convhull(x,y); % 更具所有点的坐标,计算哪些点处于凸包的边界
plot(x,y,'.','markersize',12) % 绘制所有点的位置
xlabel('Longitude')
ylabel('Latitude')
hold on
plot(x(K),y(K),'r') % 将边界上的点用红线相连
计算结果如下:

参考资料:
计算凸包 - MATLAB & Simulink - MathWorks 中国
N 维凸包 - MATLAB convhulln - MathWorks 中国


