不同条件下溶液中的物质浓度?化学反应平衡?MATLAB求解非线性方程组
一种常见的化学反应平衡关系是离子在溶液中的水解平衡,由于存在平衡常数,所以在给定条件下(温度,pH值等)能够求出溶液中盐离子和弱酸根离子的浓度。但是,化学平衡方程本身是非线性的,而且在一般情况下,溶液中存在众多的平衡体系。使得该问题的求解难度很高。例如:
已知碳酸($H_{2}CO_{3}$)溶液中存在如下水解平衡关系,计算$H^{+}$浓度为$10^{-5}$mol/L,${CO_{3}}^{2-}$浓度为$10^{-9}$mol/L时,溶液中$H_{2}CO_{3}$的浓度。
$$H^{+}+OH^{-}\rightleftharpoons H_{2}O \qquad K_{w}=10^{-14}$$
$${HCO_{3}}^{-}+H^{+}\rightleftharpoons H_{2}CO_{3} \qquad K_{a1}=4.2\times 10^{-7}$$
$${CO_{3}}^{2-}+H^{+}\rightleftharpoons {HCO_{3}}^{-} \qquad K_{a2}=5.61\times 10^{-11}$$
分析:
该问题共涉及6种物质($H^{+}$,$OH^{-}$,${CO_{3}}^{2-}$,${HCO_{3}}^{-}$,$H_{2}CO_{3}$,$ H_{2}O$),其中五种物质存在浓度($H^{+}$,$OH^{-}$,${CO_{3}}^{2-}$,${HCO_{3}}^{-}$,$H_{2}CO_{3}$),除去已知浓度的$H^{+}$和${CO_{3}}^{2-}$,还有3种物质的浓度需要求解($OH^{-}$,${HCO_{3}}^{-}$,$H_{2}CO_{3}$)。显然,该溶液体系共有三个化学平衡关系,可列出三个化学平衡方程,理论上可以求解出未知的三种物质的浓度。其化学平衡方程如下:
$$K_{w}=\left [ H^{+} \right ]\cdot \left [ OH^{-} \right ]$$
$$K_{a1}=\frac{\left [ H^{+} \right ]\cdot \left [ {HCO_{3}}^{-} \right ]}{\left [ H_{2}CO_{3} \right ]}$$
$$K_{a2}=\frac{\left [ H^{+} \right ]\cdot \left [ {CO_{3}}^{2-} \right ]}{\left [ {HCO_{3}}^{-} \right ]}$$
将已知量带入上述方程后,可以使用MATLAB中的solve方法求解该非线性方程组,代码及说明如下:
clear,clc %% matlab 求解非线性方程组 以化学反应平衡为例 CO3=10^(-9); % 已知的CO3^2-浓度 H=10^(-5); % 已知的H+浓度 kw=10^(-14); ka1=4.2*10^(-7); ka2=5.61*10^(-11); % H 和 CO3为已知量,在方程组中视为常数 syms OH HCO3 H2CO3 exp1 % 需要求解的其他3种物质(OH,HCO3,H2CO3)和需要求解的方程组(exp1)设置为符号变量 exp1=[kw==H*OH,ka1==(H*HCO3)/H2CO3,ka2==(H*CO3)/HCO3]; % 需要求解的方程组 % 非线性方程组求解方法 Y = solve(eqns,vars),其中:eqns为需要求解的方程组,vars需要求解的变量 % 注意:该问题中共存在3个方程和3个未知数,若eqns中列举了全部三个方程,则vars中必须全部列举所有未知变量才能求解 % 例如,在该问题中,若保持exp1不变,令vars=[OH HCO3],会导致无解。 % solution为结构体变量,待解变量的计算结果保存在其中,默认保存为解析解(分数表示)。 % 在该案例中分别为:solution.OH,solution.HCO3,solution.H2CO3 solution = solve(exp1, [OH HCO3 H2CO3]); % vpa方法可以将解析解(分数表示)转化为数值解(小数表示) % double方法可以将符号变量转化为数值变量 H2CO3_result=double(vpa(solution.H2CO3));
该代码的计算结果:$H_{2}CO_{3}$的浓度为0.0042 mol/L
特别的,如果想要研究$H_{2}CO_{3}$与$H^{+}$和${CO_{3}}^{2-}$之间的浓度关系,也可以用类似的方法实现。
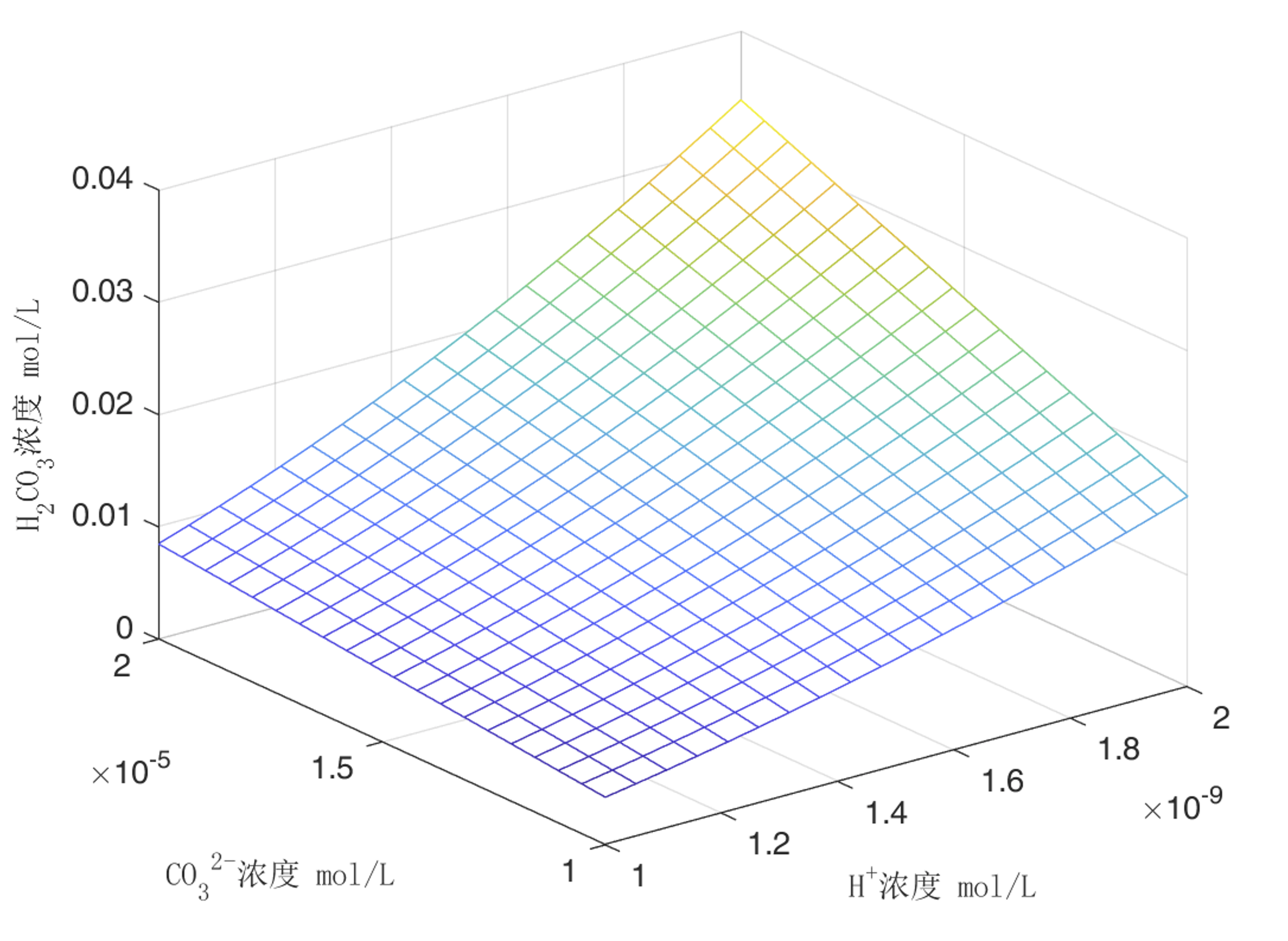
例如,可以计算出$H^{+}$浓度范围在[$10^{-5}$, $2\times 10^{-5}$] mol/L和${CO_{3}}^{2-}$浓度范围在[$10^{-9}$, $2\times 10^{-9}$] mol/L时对应的$H_{2}CO_{3}$浓度,并以$H^{+}$浓度为x轴,${CO_{3}}^{2-}$浓度为y轴,$H_{2}CO_{3}$浓度为z轴绘制三维图像进行展示。代码如下:
clear,clc
%% matlab 求解非线性方程组 以化学平衡绘图为例
num=20; % 每个维度的采样数量
H=linspace(1*10^(-5),2*10^(-5),num); % CO3^2-浓度范围
CO3=linspace(1*10^(-9),2*10^(-9),num); % H+浓度范围
H2CO3=zeros(num,num);
for indexCO3=1:num
for indexH=1:num
[H2CO3(indexCO3,indexH)]=ChemicalEquilibrium(CO3(indexCO3),H(indexH));
end
end
[X,Y] = meshgrid(CO3,H); %将其x,y轴网格化
Fig = mesh(X,Y,H2CO3); %绘制三维曲面图
xlabel('H^+浓度 mol/L','fontsize',10,'fontname','宋体');
ylabel('{CO_3}^{2-}浓度 mol/L','fontsize',10,'fontname','宋体');
zlabel('H_2CO_3浓度 mol/L','fontsize',10,'fontname','宋体');
function [H2CO3_result]=ChemicalEquilibrium(CO3,H)
kw=10^(-14);
ka1=4.2*10^(-7);
ka2=5.61*10^(-11);
syms OH H2CO3 HCO3 exp1
exp1=[kw==H*OH,ka2==(H*CO3)/HCO3,ka1==(H*HCO3)/H2CO3,];
solution = solve(exp1, [OH HCO3 H2CO3]);
H2CO3_result=double(vpa(solution.H2CO3));
end
运行结果如图所示:
参考资料:
Equations and systems solver - MATLAB solve - MathWorks 中国
特别感谢:
杨翠婷

