线性规划与非线性规划思路及案例分析（MATLAB & Lingo）

问题：

已知6种国家排放标准的汽车目前的保有量、排放因子和升级成本（升级成本指的是低于该标准的每辆汽车升级到该标准的成本，例如：国6的升级成本为15000元，意味着国1到国5标准的车升级到国6标准每辆车需要15000元）如下表所示，计算在该情况下，达到减排55%目标的升级改造成本最低的升级方案（不改变汽车保有量）。

国家排放标准	国1	国2	国3	国4	国5	国6
保有量	706	28111	52352	100804	756007	259006
排放因子（吨/量）	0.029008549	0.005805108	0.005980677	0.002081344	0.000424764	0.000283176
升级成本	0	3000	6000	9000	11000	15000

解题思路（1）：

采用非线性规划，设定升级后的国1~国6的保有量为x1~x6，设定约束条件，求解合适的x1~x6。

clear,clc
%% MATLAB非线性规划求解方法
global x0 
% 由于 matlab非线性规划函数 fmincon要求目标函数只能有一个输入和一个输出，
% 所以，其他影响目标函数值计算的变量需要通过定义为全局变量（global）实现传值
reduction=0.55;     % 减排比例
x0=[706;28111;52352;100804;756007;259006];  % 汽车保有量
A=[0.029008549,0.005805108,0.005980677,0.002081344,0.000424764,0.000283176];  % 排放因子 （吨/辆）
b=A*x0.*(1-reduction);   
% 在减排比例限制下的最大允许排放量
% 因为 MATLAB 规定线性不等式约束条件必须为 A*x<=b的形式，故采取了(1-reduction)的形式
Aeq=[1,1,1,1,1,1];
beq=Aeq*x0;
% Aeq和beq表示等式约束条件（Aeq*x=beq）
% 该处的含义为升级前后汽车总保有量不变
lb = [0,0,0,0,0,0];             % 解空间下限
ub = [beq,beq,beq,beq,beq,beq]; % 解空间上限
[x,fval,exitflag,output]= fmincon(@ObjFun,x0,A,b,Aeq,beq,lb,ub);
% fmincon 为MATLAB求解线性规划的函数
% x为规划结果（升级之后的各标准汽车的保有量），fval为规划结果对应的目标函数值
% @ObjFun为目标函数

%% 后处理方法（取得类似于整数规划的效果）
% 解释一下为什么要进行后处理以取得似于整数规划的效果
% 因为题目最终需要的求解的是车辆的升级方案，但是车辆的数量是整数，需要采用整数规划
% 但是目前 matlab 无法进行非线性的整数规划，所以只能采取变通的方式，即：
% 先使用非线性规划求解连续结果，对其结果向下取整之后，求解总量差额，将差额分别
% 添加至x的各个元素中，从新得到的解中选择效果最好的作为最终答案。
xfloor=floor(x);       % 向下取整
xfsum=sum(floor(x));
reduce=beq-xfsum;      % 计算取整之后的损失差额
cost=ones(length(A),1)*inf;
for i=1:length(A)      % 将差额分别添加至x的各个元素中，计算每种情况对应的目标函数值
    x1=xfloor;
    x1(i)=x1(i)+reduce;  
    if A*x1<=b
        [cost(i)]=ObjFun(x1);
    end
end
upIndex=find(cost==min(cost));   % 选取目标各种情况中效果最好的解作为最终结果
xfinal=xfloor;
xfinal(upIndex)=xfloor(upIndex)+reduce;  % xfinal为最终结果
sum(xfinal)

function [cost]=ObjFun(x)
global x0
x1=(x-x0);   
x1(x1<0)=0;
% 由于最终解x是升级之后的各标准汽车的保有量，故计算升级成本时需要先减去x0（初始保有量）
% 得出各标准车辆的变动量，并且由于变动量为正的代表有车辆升级为该标准，会计算成本
% 反之，变得量为负的，说明该标准车辆升级为更高标准，该变化不计算成本，故变动量（x1）
% 小于0的元素会被设置为0。
% 特别的 x1(x1<0)=0; 这步计算本身是非线性计算，所以，带有这一判断会使整个问题变为
% 非线性规划问题
c=[0;3000;6000;9000;11000;15000];  % 升级成本
cost=x1'*c;
end

分析：

非线性规划的思路简洁明了，借助MATLAB代码进行实现也并不困难，但是该技术路线并不完美，主要的存在以下三个问题：

（1）非线性规划的求解难度远高于线性规划，并且非线性规划本身不能完全保证其结果的全局最优性。在复杂问题背景下，非线性规划的求解难度会很高，所得出的解的质量也难以保证。

（2）MATLAB求解非线性规划的函数fmincon为其专有方法，也就意味着，该解题思路几乎仅能通过MATLAB实现，而不容易向其他平台（如C#、python等）迁移。

（3）该问题本身为整数规划问题，而MATLAB无法直接处理目标函数或约束条件为非线性的整数规划问题，不能保证其得出的连续解与题目要求的离散解（整数解）在全局最优处的一致性，并且后处理过程使用的贪心算法在面临复杂情况（例如：解空间很大，取整差额较多时）难以保证得出全局最优解（一定要尽可能取得全局最优的话可以考虑进行穷举，但是在解空间很大，取整差额较多时，穷举法并不适用）。

所以，需要转变思路并设计一种方法，将非线性规划问题转变为线性规划问题，并且能够进行整数规划。

解题思路（2）：

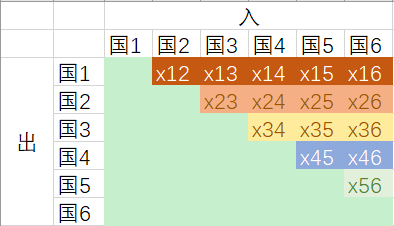
一般情况下，将非线性问题转换为线性规划问题都是比较困难的。该问题显示为非线性规划的核心原因是在计算车辆的变动差额时，需要判断差额的正负性，并且将负值置为0，该过程为非线性过程，正是该过程的存在使得目标函数变为非线性函数。一种可行的方法是，将各排放标准车辆之间的变动量作为求解变量，即问题变为达到减排55%目标时，求解出国1升级为国2、国3、国4、国5和国6的车辆数目（分别为x12、x13、x14、x15、x16）、国2升级为国3、国4、国5和国6的车辆数目（分别为x23、x24、x25、x26）等，如图所示：

整数规划问题可以通过使用Lingo进行解决，Lingo代码如下：

model:
sets:
demand/1..6/:x0,A,c;
supply/1..1/:allcar,reduction;
endsets
data:
x0=706 28111 52352 100804 756007 259006;
A=0.029008549 0.005805108 0.005980677 0.002081344 0.000424764 0.000283176;
c=0 3000 6000 9000 11000 15000;
allcar=1196986;
reduction=0.55;
enddata

!目标函数;
min=(x16+x26+x36+x46+x56)*c(6)+(x15+x25+x35+x45)*c(5)+(x14+x24+x34)*c(4)+(x13+x23)*c(3)+x12*c(2);

!第一约束条件（减排量要符合要求）;
(x0(1)-(x12+x13+x14+x15+x16))*A(1)+(x0(2)-(x23+x24+x25+x26)+x12)*A(2)+(x0(3)-(x34+x35+x36)+x13+x23)*A(3)+(x0(4)-(x45+x46)+x14+x24+x34)*A(4)+(x0(5)-(x56)+x15+x25+x35+x45)*A(5)+(x0(6)+x16+x26+x36+x46+x56)*A(6)<=1101.044469866*(1-reduction(1));

!第二约束条件（某标准的升级车辆不能超过该标准目前的保有量）;
(x12+x13+x14+x15+x16)<=x0(1);
(x23+x24+x25+x26)<=x0(2);
(x34+x35+x36)<=x0(3);
(x45+x46)<=x0(4);
x56<=x0(5);

!第三约束条件（车辆保有量不能为负）;
x12>=0;
x13>=0;
x14>=0;
x15>=0;
x16>=0;
x23>=0;
x24>=0;
x25>=0;
x26>=0;
x34>=0;
x35>=0;
x36>=0;
x45>=0;
x46>=0;
x56>=0;
!进行整数规划;
@gin(x12);
@gin(x13);
@gin(x14);
@gin(x15);
@gin(x16);
@gin(x23);
@gin(x24);
@gin(x25);
@gin(x26);
@gin(x34);
@gin(x35);
@gin(x36);
@gin(x45);
@gin(x46);
@gin(x56);

end

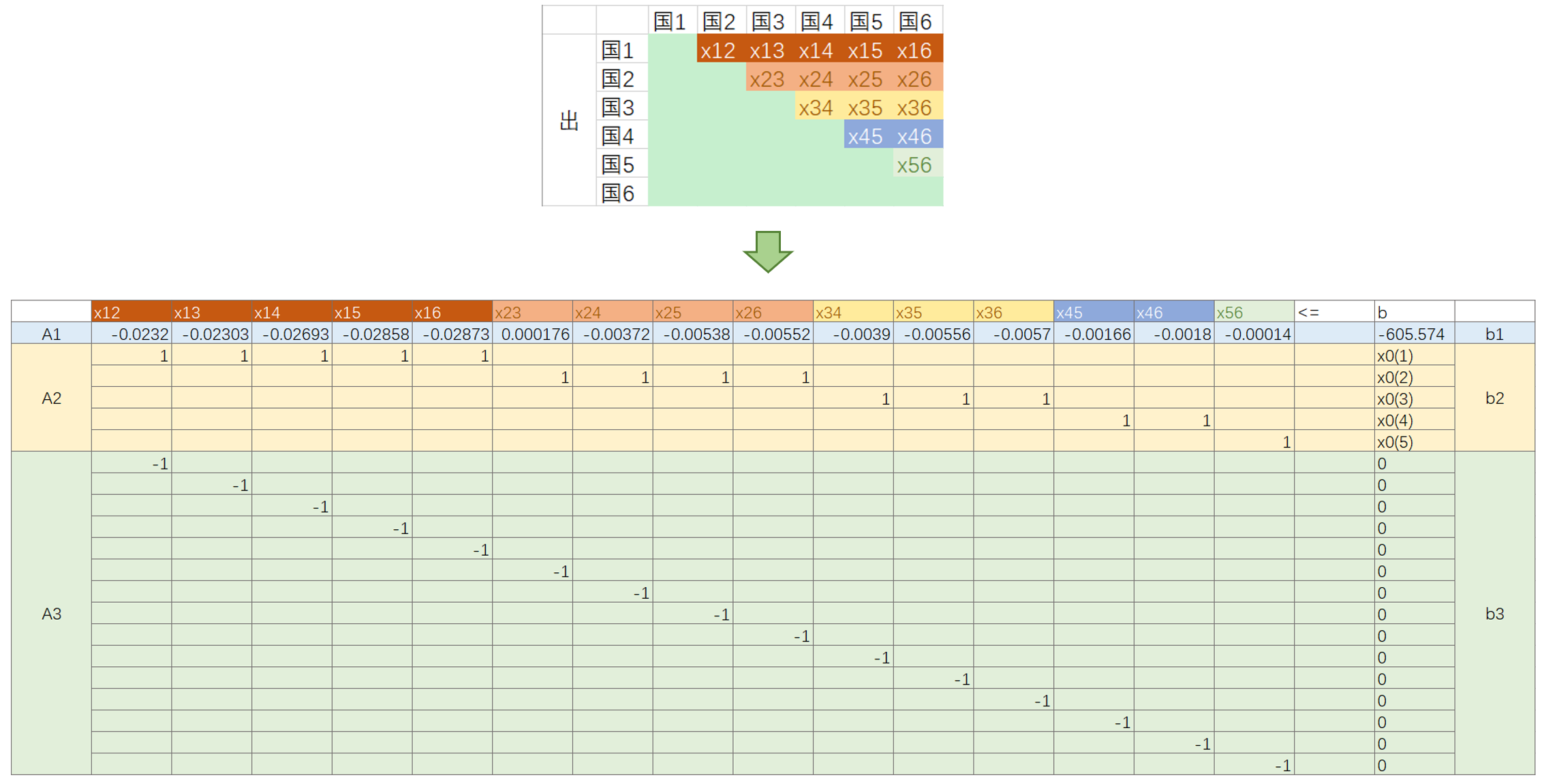
参照Lingo的求解逻辑，可以设计MATLAB代码进行混合整数线性规划求解。但要注意，MATLAB的混合整数线性规划函数（intlinprog）以及线性规划函数（linprog）均需要自行编制约束条件矩阵（A，b），解向量以及约束条件设置方式如图所示：

clear,clc
%% MATLAB 混合整数线性规划求解方法
reduction=0.55;
x0=[706;28111;52352;100804;756007;259006];  % 汽车保有量
A0=[0.029008549,0.005805108,0.005980677,0.002081344,0.000424764,0.000283176];  % 排放因子 （吨/辆）
c=[0;3000;6000;9000;11000;15000];  % 升级成本
xRank=length(x0)-1;
pRank=xRank:-1:1;
qRank=1:xRank;
xNum=sum(pRank);
%% 计算第一约束条件（减排量要符合要求）
A1=zeros(1,xNum);
n=1;
m=1;
p=pRank(n);
for i=1:xNum
    if i>p
        qRank=1+n:xRank;
        n=n+1;
        p=p+pRank(n);        
        m=1;
    end
%     disp([num2str(qRank(m)+1),'_',num2str(n)])
    A1(i)=A0(qRank(m)+1)-A0(n);
    m=m+1;
end
b1=A0*x0.*(-1).*reduction;
%% 计算第二约束条件（某标准的升级车辆不能超过该标准目前的保有量）
A2=zeros(xRank,xNum);
n=1;
p=pRank(n);
for i=1:xNum
    if i>p
        n=n+1;
        p=p+pRank(n);
    end
    A2(n,i)=1;
end
b2=x0(1:xRank);
%% 计算第三约束条件（车辆保有量不能为负）
A3=eye(xNum,xNum);
A3=-1.*A3;
b3=zeros(xNum,1);

A=[A1;A2;A3];
b=[b1;b2;b3];

%% 计算目标函数（成本最低）
f=zeros(1,xNum);
n=1;
m=1;
p=pRank(n);
qRank=1:xRank;
for i=1:xNum
    if i>p
        qRank=1+n:xRank;
        n=n+1;
        p=p+pRank(n);        
        m=1;
    end
%     disp(num2str(qRank(m)+1))
    f(i)=c(qRank(m)+1);
    m=m+1;
end
% x=linprog(f,A,b); % 常规线性规划
intcon=1:xNum;      % 用于标记解向量xfinal中哪些自变量为整数，例如：intcon=[2,5];则解向量中排序第2和第5的自变量限定为整数
[xfinal,fval]=intlinprog(f,intcon,A,b); % 混合整数线性规划

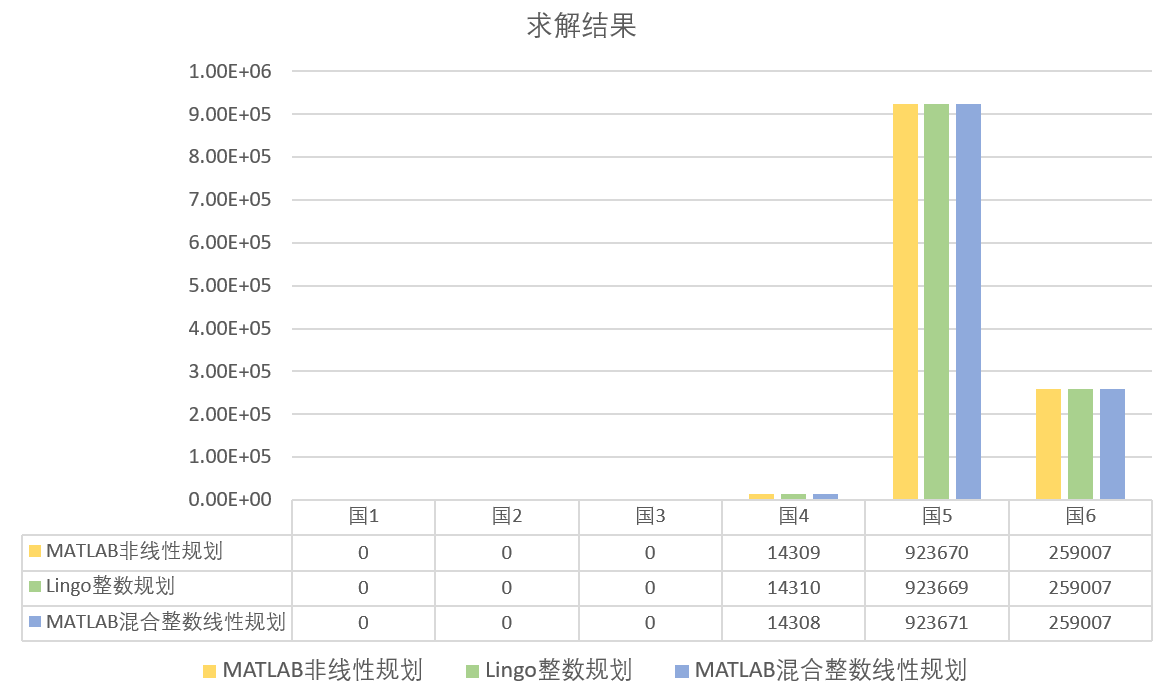
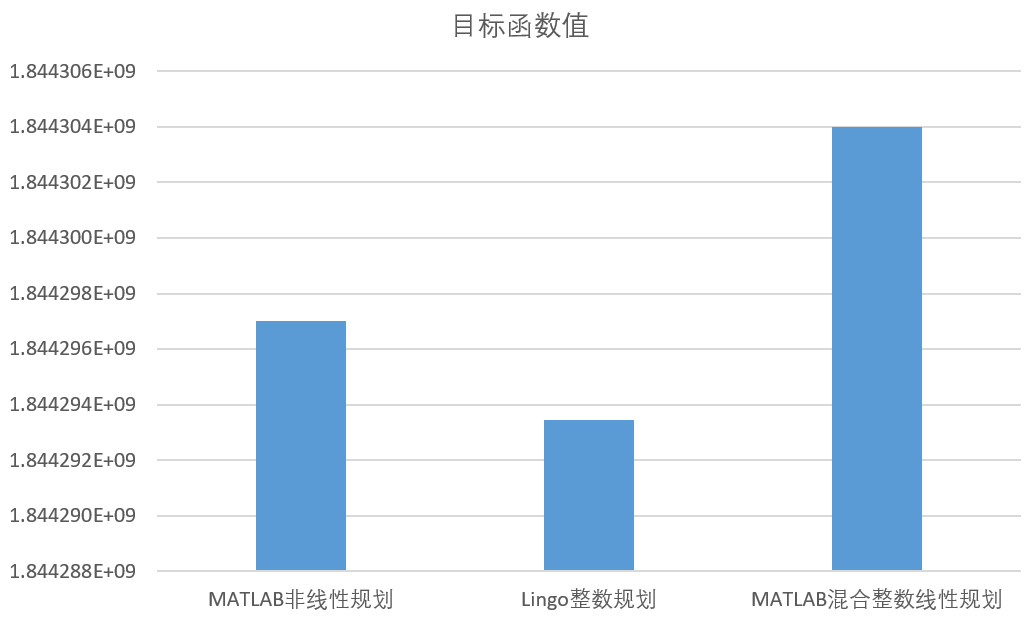
从求解结果来看，三种求解方法所得方案差异很小（仅国4和国5标准的汽车数目存在少量差异），目标函数值差异也很小。但是Lingo的求解效果最好，其次是MATLAB非线性规划，最后是MATLAB混合整数线性规划。

 

 

 

参考资料：

混合整数线性规划 (MILP) - MATLAB intlinprog - MathWorks 中国

 

特别感谢：

龙老师，贺玉瑶