Pearson（皮尔逊）相关系数与Spearman（斯皮尔曼）相关系数及其SPSS实现
Pearson（皮尔逊）相关系数：
又称相关系数或线性相关系数，一般用字母r表示，定义式：
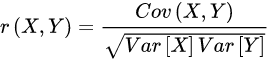
特性：两个变量的位置和尺度的变化不会引起该系数的改变，即把X移动到a+bX和把Y移动到c+dY（其中a、b、c、d为常数）并不会改变相关系数（该结论在总体和样本皮尔逊相关系数中都成立）。
Spearman（斯皮尔曼）相关系数（秩相关系数）：
又称斯皮尔曼等级相关系数，常用希腊字母ρ表示。其利用单调方程评价两个统计变量的相关性。 如果数据中没有重复值， 并且当两个变量完全单调相关时，斯皮尔曼相关系数则为+1或−1。定义式：
结论：无参数的等级相关系数，亦即其值与两个相关变量的具体值无关，而仅仅与其值之间的大小关系有关。di表示两个变量分别排序后成对的变量位置差，N表示N个样本，减少异常值的影响。
SPSS实现：
案例数据如图所示：
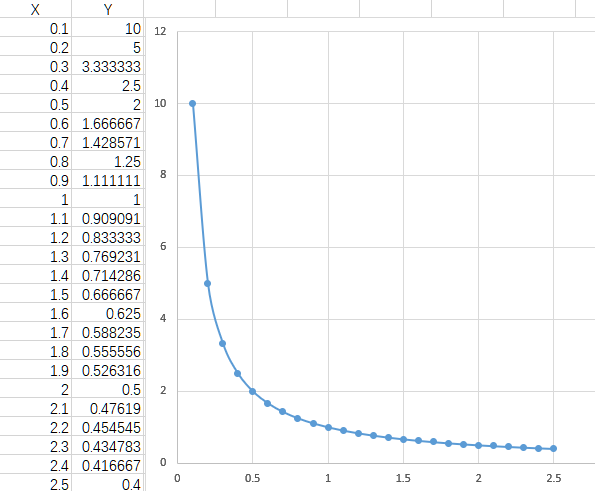
打开SPSS，读入案例数据，分析 > 相关 > 双变量...
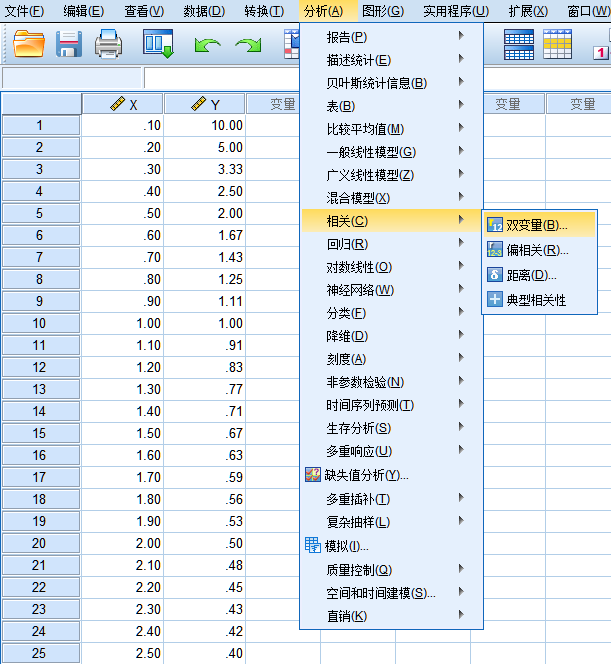
在“双变量相关性”对话框中选取变量“X”和“Y”，在“相关系数”处勾选“皮尔逊”和“斯皮尔曼”，单击确定。
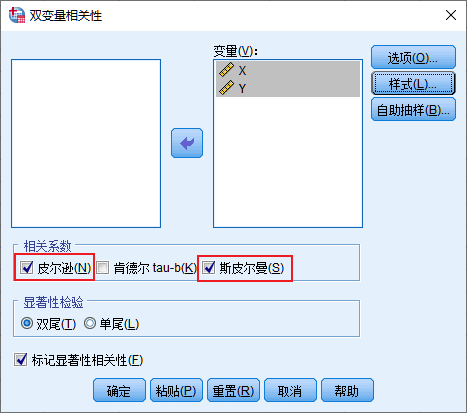
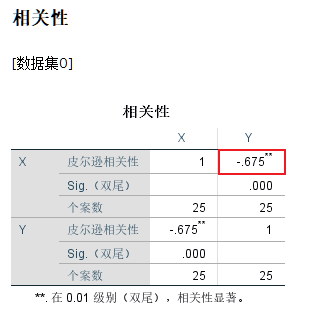
结果如图所示，在相关性表中展示的是Pearson（皮尔逊）相关系数。由于案例数据展示的是非线性关系，故变量“X”与“Y”间的相关系数仅为-0.675。
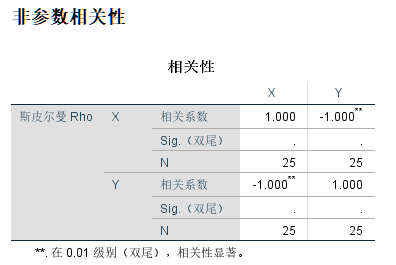
非参数相关性表中展示的是Spearman（斯皮尔曼）相关系数，由于随着“X”的增长，“Y”严格单调递减，各变量序列数值的位次（秩）对应严格相反（“X”中最大的值对应“Y”中最小的值），故变量“X”与“Y”间的秩相关系数为-1。
参考资料：
https://baike.baidu.com/item/%E7%9A%AE%E5%B0%94%E9%80%8A%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0
https://baike.baidu.com/item/spearman%E7%9B%B8%E5%85%B3%E7%B3%BB%E6%95%B0/7977847?fr=aladdin
https://jingyan.baidu.com/article/3a2f7c2ed8481426aed61165.html
