定位柱和定位孔的尺寸,相关设计讲述
为了提高两个零部件装配时的位置精度,我们经常需要在二者之间设计定位柱和定位孔,以减少累积尺寸误差。
然而,正确设计定位柱与定位孔不是一件容易的事情,我们需要考虑诸多问题,例如,定位柱与定位孔的间隙多少最好?为什么要用腰型孔?腰型孔与定位柱的间隙是多少?这些有理论依据吗?
本文将通过公差分析的理论计算来回答上述问题。
— 1—
定位柱和定位孔的间隙
在设计定位柱和定位孔之间的间隙时,需要考虑两个原则:
1)间隙需要足够小,以减少定位柱在定位孔中的晃动,从而增加定位精度。否则,定位柱在定位孔中会发生较大晃动,起不到定位效果。
2)间隙也不能太小,以确保定位柱和定位孔装配时不发生干涉。否则,当定位柱尺寸偏大以及定位孔尺寸偏小时,定位柱会装不进定位孔。
简单来说说,就是:在定位柱能够装进定位孔的情况下,间隙设计得越小越好。
间隙越小,定位精度越高。同时,间隙不能太小,否则会装不上。
定位柱和定位孔之间所允许的最小间隙,我们可以通过公差分析进行计算。
例,如图5所示,两个零件通过圆形定位柱和定位孔进行定位;定位柱外径为3.90mm,公差为±0.05mm,定位孔的公差为±0.05mm,那么定位孔的最小尺寸为多少?这转化为公差分析时的计算要求是:当定位柱尺寸最大、同时定位孔尺寸最小时,二者的间隙需要大于等于0。
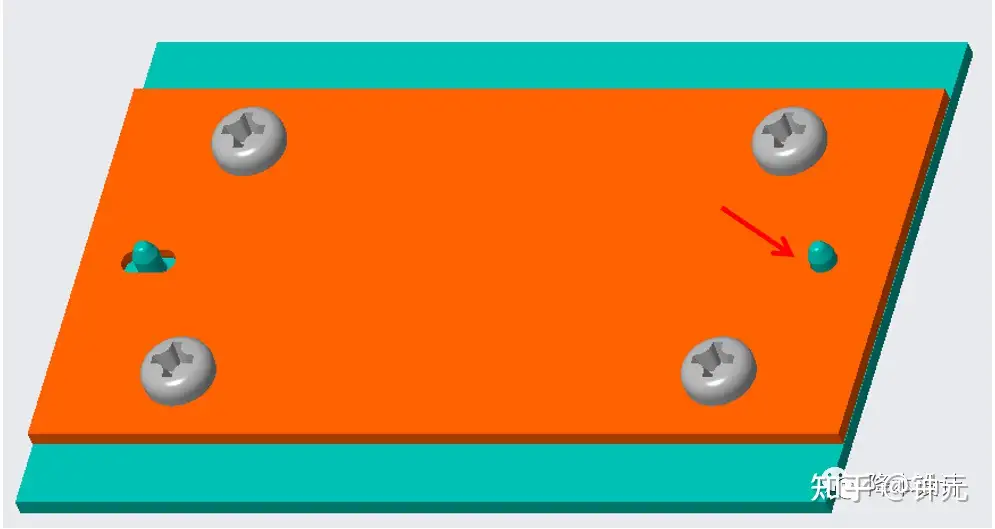
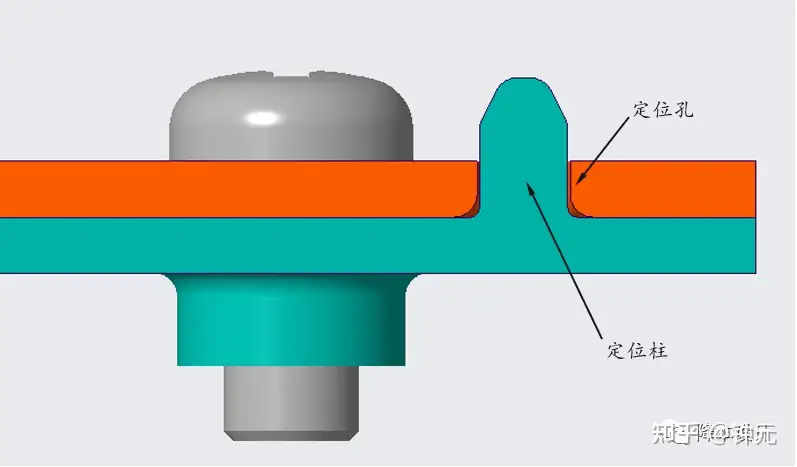
▲图5--定位柱和定位孔的设计
如图6所示,我们采用极值法,计算结果为定位孔尺寸为4.00±0.05mm,这意味着:当定位柱尺寸最大3.90+0.05=3.95mm、定位孔尺寸最小4.00-0.05=3.95mm时、定位柱依然能够装配进入定位孔。
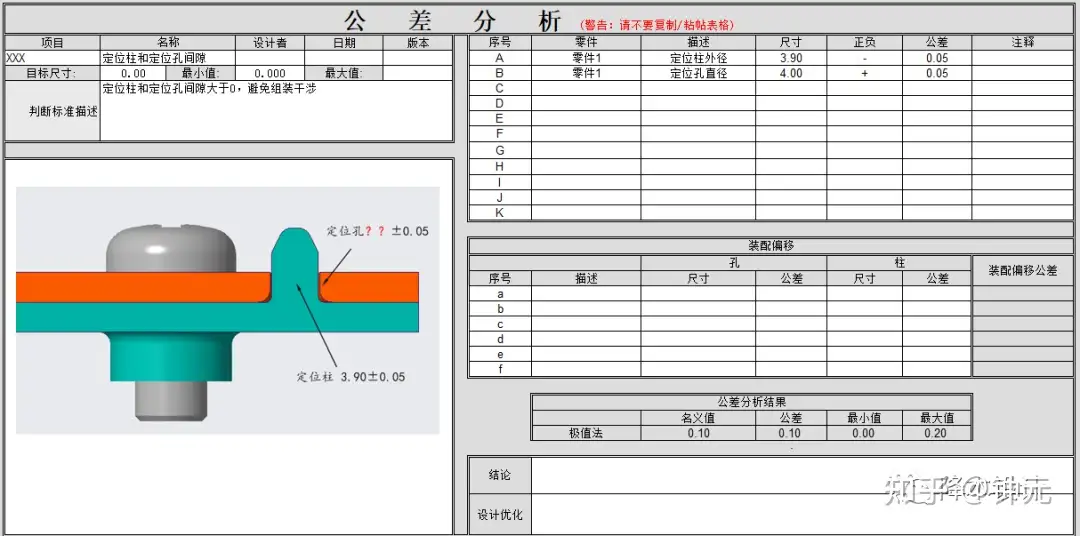
▲图6--极值法计算
如图7所示,均方根法的计算结果为:定位孔的尺寸该为3.97±0.05mm。
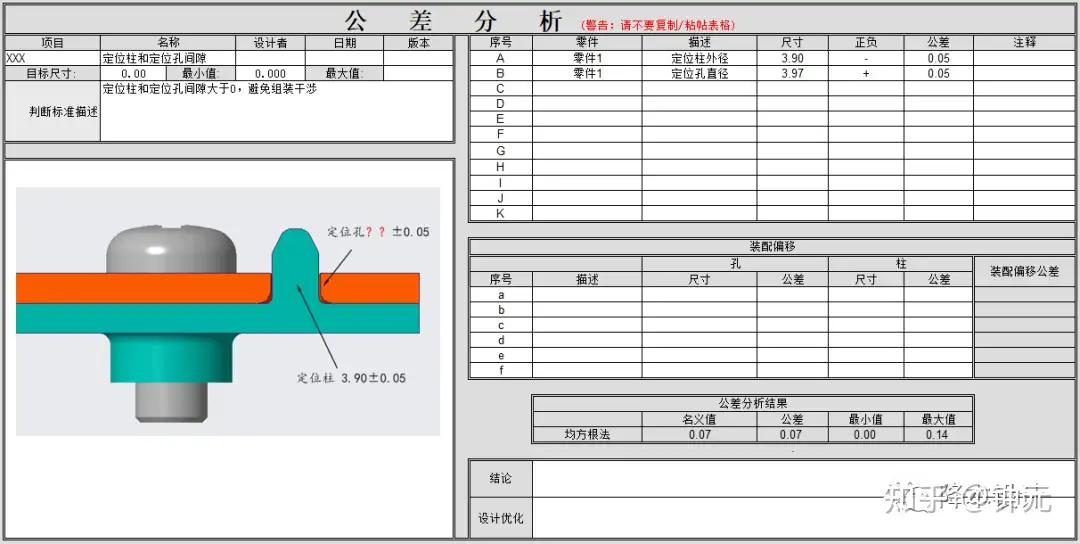
▲图7--均方根法计算
如果我们并不需要如此高的装配精度,那么可以适当增加定位孔的尺寸,把定位孔和定位柱的间隙增加。
— 2—
为什么要用腰型孔
我们是不是可以使用两个一模一样的圆形定位柱和定位孔进行定位呢?如图8所示。我看到很多工程师是这样去设计的。


▲图8--圆形定位柱和定位孔
显然这样不行,这会发生过定位,造成一个定位柱装进一个定位孔之后,另一个定位柱有可能就装不进去了。
一个定位柱和一个定位孔,在X和Y坐标轴上约束了两个零件的相对位置。
如果是两个定位柱和定位孔,那么在X方向就约束了两次,X方向发生了过定位,如图9所示。
当两个定位柱之间的尺寸偏大、同时定位孔之间的尺寸偏小时,或者两个定位柱之间的尺寸偏小、同时定位孔之间的尺寸偏大,就有可能发生装不上的现象。
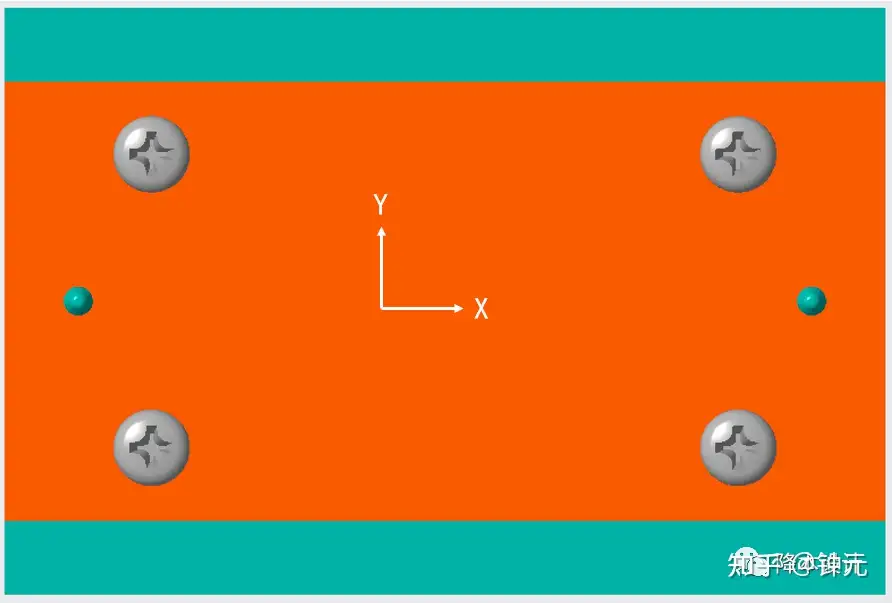

▲图9--过定位发生了
我们可通过公差分析的实际计算来说明,为什么会发生装不上的现象。
如图10所示,我们假设右侧定位柱定位孔先组装好,再来计算左侧定位柱和定位孔的间隙。
计算结果显示,使用极值法,左侧定位柱和定位孔的间隙为0.05±0.75mm,则最小间隙为0.05-0.75mm=-0.7mm,这意味着会发生0.7mm的干涉;使用均方根法,间隙为0.05±0.44mm,这意味着会发生0.39mm的干涉;均会出现装不上的现象。
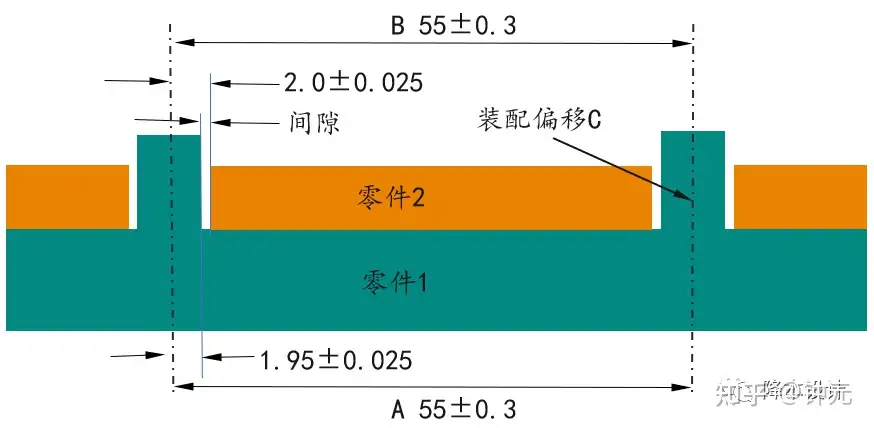
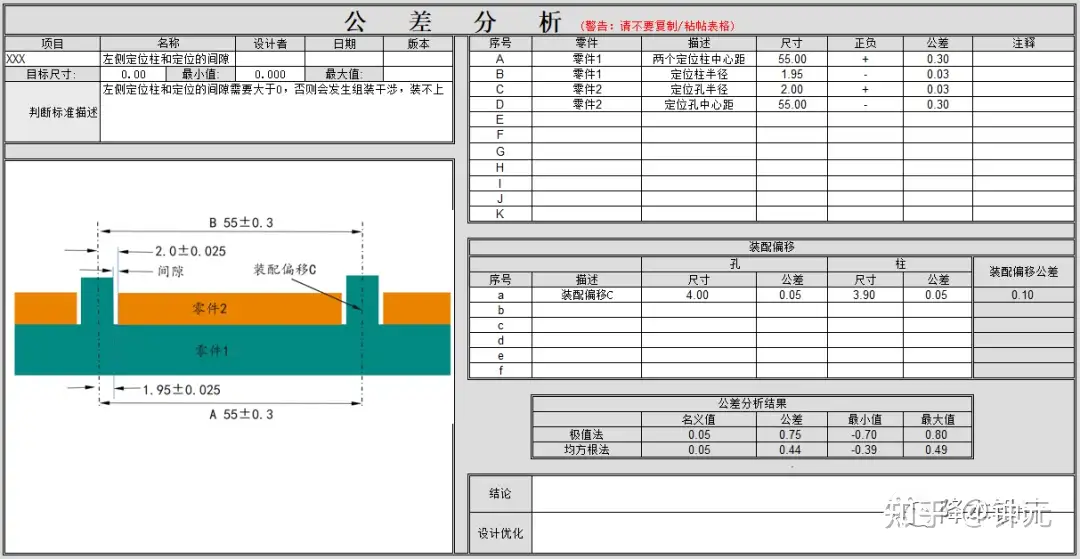
▲图10--过定位计算
— 3—
定位柱与腰型孔的间隙是多少
两个定位柱和定位孔都是圆形,会发生过定位,造成干涉。我们需要把一个定位孔改成长圆孔或腰型孔,避免X方向过定位,如图11所示,



▲图11--腰型孔,避免过定位
腰型孔的尺寸如何设计呢?
通过上一节的计算结果,我们需要把当前左侧2.00mm直径的定位孔尺寸增加,直到其与定位柱的间隙始终大于等于0。
如图12所示,如果采用极值法,腰型孔的直径需要增加到2.70mm。
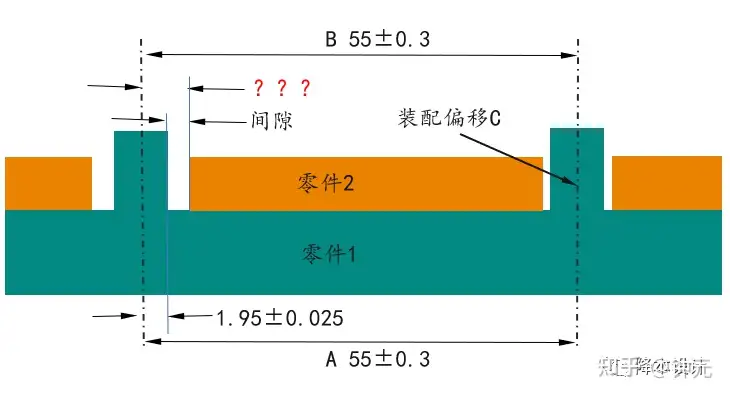
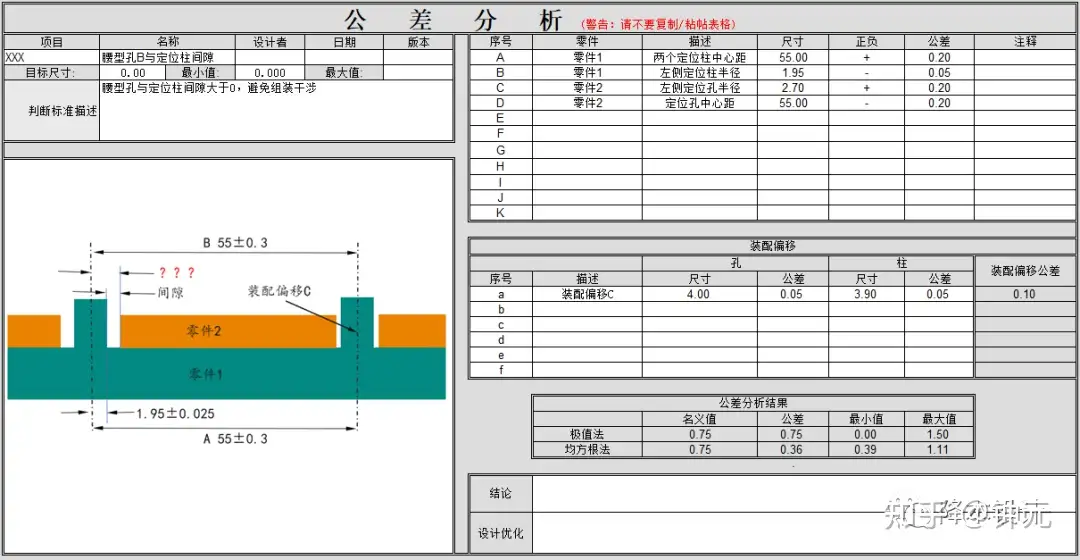
▲图12--腰型孔尺寸计算(极值法)
如图13所示,如果采用均方根法,腰型孔的直径需要增加到2.31mm。
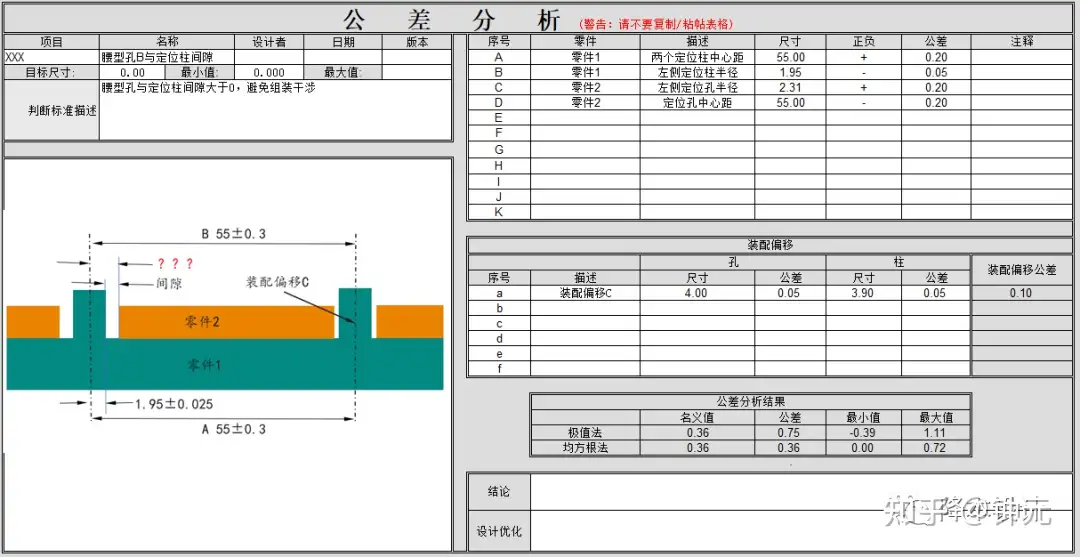
▲图13--腰型孔尺寸计算(均方根法)
注1:本文中的公差分析具体计算涉及到装配偏移,关于装配偏移的定义以及详细的算法,请参考《面向制造和装配的产品设计指南》一书,本文篇幅有限。也请浏览本文的工程师,不要私信我解释什么是装配偏移。相信我,书中解释更全面。
注2:本文中的公差分析仅考虑了1维线性尺寸;
注3:本文中的公差分析仅考虑了尺寸公差,未包括形位公差;
最后的话
产品结构设计中的每一个特征、每一个尺寸、每一个公差等,都不是随意设计的;而是基于一定的理论基础,例如公差分析。作为工程师,我们需要具备一定的公差分析能力。
PS:大家如果需要本文中的公差分析计算实例EXCEL表格,欢迎添加我的企业微信,或者微信我。(人数较多,不一定会及时回复,请见谅)



