OpenGL学习之路（二）

1　引子

在上一篇读书笔记中，我们对书本中给出的例子进行详细的分析。首先是搭出一个框架；然后填充初始化函数，在初始化函数中向OpenGL提供顶点信息（缓冲区对象）和顶点属性信息（顶点数组对象），并启用顶点数组对象；最后填充绘制函数，首先清空颜色缓存，然后调用glDrawArray来绘制基本图形。例子中使用的坐标都是二维坐标，所以画出来的图形是二维图形（这里是两个三角形），而我们知道OpenGL最主要是用来进行三维图形的渲染的，所以有必要在学习OpenGL相关API之前对三维变换做一个简要的介绍。其实这一部分应该属于红宝书中第五章的内容，这里我们将其提前了，在读书笔记（二）就拿出来介绍——这是我们三维渲染的最基本的知识点，也是最关键的知识点，理解起来也有一定的难度。本次读书笔记主要讲述平移、旋转、缩放变换的变换矩阵，投影变换将在下一篇读书笔记再做记录。本篇读书笔记主要是自己对一些数学概念的理解和记录，仅供参考，如有不同理解的，大家可以一起讨论哈！

2　 点、坐标系与向量

讨论三维变换之前，得先了解点、向量和坐标系这些基本数学概念。这部分内容可能比较抽象，下面记录的是我对这些概念的一些理解。

2.1　位置的相对性

在日常生活中，我们在向别人描述一个陌生的地方的时候，通常会选择一个他熟悉的地方作为一个参考点。例如：我们向老外介绍河北的一座古城邯郸，老外知道北京，我们就会说邯郸在北京往西南走300km；如果老外知道石家庄，那我们也可以告诉他，邯郸在石家庄往南走100km。这说明，位置是一个相对的概念，要描述一个位置，首先要选择参考点；参考点的选择是任意的，所选取的参考点不同，位置的描述也就不同。

在几何中，位置用“点”这一概念来描述，即点是一个只有位置没有大小的量。描述一个点和描述一个位置是一回事，刚才已经说了位置是一个相对的概念，所以首先就要用到参考点。我们以最简单的一维数轴为例来说明描述点的位置，如下图所示：

对于数轴上同一点$A$，要描述$A$点的位置，先要选取任意一个参考点，如果选择的参考点是$O_1$，则$A$点在$O_1$点右边$l_1$的地方；如果选择的参考点是$O_2$，则$A$点在$O_2$点左边$l_2$的地方。通过数轴和参考点，我们就将数轴上的几何点用抽象的数字表达出来了。

2.2 坐标系与向量

从图上可以看出，数轴上的点只能沿着数轴方向进行变化，即它是一维的。如果点在一个平面上或一个空间中变化，那么数轴这一工具是无法描述的。这时就要引入二维坐标系和三维坐标系来描述点的位置。介绍坐标系之前，首先介绍一下向量的概念。

在我们还是十七八岁学习高一几何的时候，我们就已经接触到了向量——既有大小，又有方向的量，用一个有向线段来表示。说白了，向量定义了一个方向、一个长度和一个单位长度。如上图中，$O_1A$和$AO_2$就是两个向量，大小分别为$l_1$和$l_2$，方向为水平向右。

一个平面上，有无数这样的向量。但是关于向量，有一个非常重要的法则——使用平行四边形法则来对任何一个向量进行分解。平行四边形法则来自于物理学中力的分解与合成，后被引入数学中加以抽象来描述向量的分解与合成。所谓平行四边形法则，指的是任何一个平面向量都可以用一个不共线的两个向量表示。于是，平面中无数的向量就可以用两个不共线的向量来表示。由这两个向量及它们的公共起点构成的数学结构就是二维坐标系，用坐标系就可以描述二维平面上的任意点，当然也可以描述二维平面上的任意向量，这两个向量就是线性代数中的基向量。我们知道，在数学中，向量是位置无关的（即自由向量），只要大小相等，方向相同的两个向量就是同一个向量（这和物理学中的力不一样）。所以要描述二维空间中的点，还需要一个参考点，于是就定义了这两个向量的公共起点作为参考点——即我们熟知的坐标原点。坐标轴向量和坐标原点就构成了坐标系，可以用坐标系来描述其中的任何向量和任一点。

三维坐标系和二维坐标系是类似的，使用两次平行四边形法则，从而将任意一个三维向量表示为三个不共面的三维向量(基向量)来表示，这三个向量移到一起的公共起点定义为三维坐标系的坐标原点。二维和三维笛卡尔坐标系就是基向量垂直的二维和三维坐标系，也是应用最为广泛的坐标系，也称为平面直角坐标系和空间直角坐标系。

下面，我们来看看向量的表示方法。同样在我们懵懵懂懂的青春岁月里，我们就已经知道向量有两种表示方法：第一种是符号表示法，如$\mathbf{a}, \mathbf{b}$等；另一种是坐标表示法，这里对坐标表示做较详细的说明。刚才已经说了，任意一个二维向量都可以用两个不共线的向量来表示，假设两个基向量为$\mathbf{i}$和$\mathbf{j}$，且长度为1。则对任一个向量$\mathbf{a}=x_a\mathbf{i} + y_a\mathbf{j}$，这样，向量$\mathbf{a}$可用一个有序对$(x_a, y_a)$来唯一表示，这就是向量的坐标表示。三维乃至$N$维向量的坐标表示都是一样的。在这里，博主还是想强调一下，向量的坐标并不是该向量在坐标轴上的投影，只有笛卡尔坐标是向量在基向量上的投影。所以，在普通坐标系下，一个向量的坐标不是很好求，但在直角坐标系下，就变得很好求了——求投影，这也是笛卡尔坐标系应用的如此广泛的原因。下面我们来看看，什么是投影，其实高一数学中也已经接触到了，如下图所示：

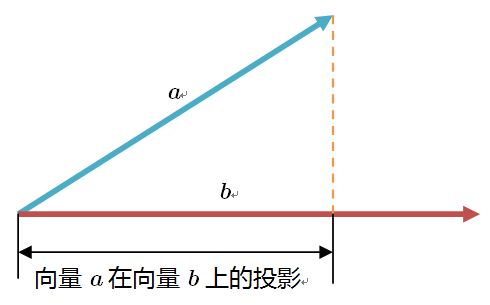
假设$c$为向量$\mathbf{a}$在向量$\mathbf{b}$上的投影，那么：

\begin{equation} c = \mathbf{a} \cos<\mathbf{a}, \mathbf{b}>\end{equation}

所以，在二维直角坐标系中，如果二维向量$\mathbf{a}$长度为$l$，该向量与$x$轴和$y$轴的夹角分别为$\alpha$和$\beta$，则我们很容易得到该向量的坐标表示为$\mathbf = (l\cos\alpha, l\cos\beta)^\text{T}$；同样地，对三维空间向量$\mathbf{b}$，其长度为$L$，与$x$轴、$y$轴和$z$轴的夹角分别为$\alpha$、$\beta$和$\gamma$，则其坐标表示为$\mathbf{b}=(L\cos\alpha, L\cos\beta, L\cos\gamma)^\text{T}$。

2.3 点的表示

刚才我们定义了坐标系——坐标原点和三个不共面的向量组成，并且三维空间中的任意向量都可以由这三个向量唯一表示，但我们没有讲点怎么由坐标系来定义。设在三维笛卡尔坐标系中，坐标原点为$O$，三个基向量分别为$\mathbf{i}$，$\mathbf{j}$，$\mathbf{k}$，我们要求$P$点的坐标，那么

$$\vec{OP} = x_{1}\mathbf{i} + y_{1}\mathbf{j} + z_{1}\mathbf{k}$$

于是，点$P$可以表示为

$$P = x_{1}\mathbf{i} + y_{1}\mathbf{j} + z_{1}\mathbf{k} + \mathbf{O}$$

所以，要想表示一个三维的点，可以用四维坐标来表示，例如刚才的$P$可以表示为$P = (\begin{array}{cccc} x_1 & y_1 & z_1 & 1\end{array})$，这就是齐次坐标。对顶点来说，齐次坐标才是其真正的表示方式。向量可以表示为$\mathbf{v} = (\begin{array}{cccc} x_1 & y_1 & z_1 & 0\end{array})$。

3　线性变换与齐次坐标

3.1 概述

代数中的线性变换的概念很抽象，涉及到向量空间、线性映射之类的概念，在这里不做过多解释，如下想了解可以度娘或必应。给一个通俗点的解释，三维线性变换就是将点/向量的坐标值做一个运算，使其坐标值发生改变，这在几何中的反映就是几何体的形状被改变了。在计算机图形学中，线性变换一般是指平移、旋转、缩放、投影（正交投影和透视投影）以及这些基本变换的综合运算。通过刚才的描述，我们知道一下几点信息：几何中的点或向量由四个坐标值确定，而坐标值是由坐标系确定的，坐标系又是由三个不共面的向量和坐标原点构成。也就是说，对于同一点，在不同的坐标系下，描述它的坐标值是不一样的，而变换就是建立这两种不同描述之间的联系——所以在以前我们称之为坐标变换。例如：在坐标系$\mathbf{O}_1-\mathbf{i}_1\mathbf{j}_1\mathbf{k}_1$坐标系下，某一点可以描述为$P$点可以用四元祖$(x_1, y_1, z_1, o_1)$描述，

\begin{equation}\label{p2}P = \begin{array}{cccc} (x_1 & y_1 & z_1 & o_1)\end{array}\left(\begin{array}{c}\mathbf{i}_1 \\ \mathbf{j}_1 \\ \mathbf{k}_1 \\ \mathbf{O}_1\end{array}\right) = (\begin{array}{cccc} \mathbf{i}_1 & \mathbf{j}_1 & \mathbf{k}_1 & \mathbf{o_1}\end{array})\left(\begin{array}{c}x_1 \\ y_1 \\ z_1 \\ o_1 \end{array}\right)\end{equation}

在另一个坐标系为$\mathbf{O}_2-\mathbf{i}_2\mathbf{j}_2\mathbf{k}_2$，可以用另一个有序元组描述它，设为$(x_2, y_2, z_2, o_2)$

\begin{equation}\label{p1}P = \begin{array}{cccc} (x_2 & y_2 & z_2 & o_2)\end{array}\left(\begin{array}{c}\mathbf{i}_2 \\ \mathbf{j}_2 \\ \mathbf{k}_2 \\ \mathbf{O}_2\end{array}\right) = (\begin{array}{cccc} \mathbf{i}_2 & \mathbf{j}_2 & \mathbf{k}_2 & \mathbf{O_2}\end{array})\left(\begin{array}{c}x_2 \\ y_2 \\ z_2 \\ o_2 \end{array}\right)\end{equation}

那么怎么建立$(\ref{p1})$和$(\ref{p2})$之间的联系呢？还是之前我们说的，任意一个三维向量都可以表示用三个不共面的向量表示，所以$\mathbf{i}_2, \mathbf{j}_2, \mathbf{k}_2$可以用$\mathbf{i}_1, \mathbf{j}_1, \mathbf{k}_1$线性表出：

$$\mathbf{i}_2 = T_{11} \mathbf{i}_1 + T_{21} \mathbf{j}_1 + T_{31} \mathbf{k}_1 + 0 \mathbf{O}_1$$

$$\mathbf{j}_2 = T_{12} \mathbf{i}_1 + T_{22} \mathbf{j}_1 + T_{32} \mathbf{k}_1 + 0 \mathbf{O}_1$$

$$\mathbf{k}_2 = T_{13} \mathbf{i}_1 + T_{23} \mathbf{j}_1 + T_{33} \mathbf{k}_1 + 0 \mathbf{O}_1$$

$$\mathbf{O}_2 = T_{14} \mathbf{i}_1 + T_{24} \mathbf{j}_1 + T_{34} \mathbf{k}_1 + T_{44} \mathbf{O}_1$$

 即：

$$(\begin{array}{cccc}\mathbf{i}_2 & \mathbf{j}_2 & \mathbf{k}_2 & \mathbf{O}_2 \end{array}) = (\begin{array}{cccc}\mathbf{i}_1 & \mathbf{j}_1 & \mathbf{k}_1 & \mathbf{O}_1 \end{array})\left(\begin{array}{cccc}T_{11} & T_{12} & T_{13} & T_{14} \\T_{21} & T_{22} & T_{23} & T_{24}\\T_{31} & T_{32} & T_{33} & T_{34}\\0 & 0 &0& T_{44}\end{array}\right)$$

于是，我们就可以写出从$(\begin{array}{cccc}x_1 & y_1 & z_1 & o_1 \end{array})^{\text{T}}$变换到$(\begin{array}{cccc}x_2 & y_2 & z_2 & o_2 \end{array})^{\text{T}}$的变换表达式为：

$$\left(\begin{array}{c}x_2 \\ y_2 \\ z_2 \\ o_2 \end{array}\right) = (\begin{array}{cccc}\mathbf{i}_1 & \mathbf{j}_1 & \mathbf{k}_1 & \mathbf{O}_1 \end{array})\left(\begin{array}{cccc}T_{11} & T_{12} & T_{13} & T_{14} \\T_{21} & T_{22} & T_{23} & T_{24}\\T_{31} & T_{32} & T_{33} & T_{34}\\0.0 & 0.0 &0.0& T_{44}\end{array}\right)\left(\begin{array}{c}x_1 \\ y_1 \\ z_1 \\ o_1 \end{array}\right) $$

其中，将

$$T=\left(\begin{array}{cccc}T_{11} & T_{12} & T_{13} & T_{14} \\T_{21} & T_{22} & T_{23} & T_{24}\\T_{31} & T_{32} & T_{33} & T_{34}\\0.0 & 0.0 &0.0& T_{44}\end{array}\right)$$

称为坐标变换矩阵。接下来主要就是讲解怎么求基本的坐标变换(仿射变换)矩阵。

3.2 缩放

缩放应该是所有线性变换中最简单的变换了。执行缩放操作，例如将一个向量缩放为原来的$s$倍，相当于原点不变，$x$、$y$、$z$三个坐标轴缩放为原来的$s$倍。根据3.1介绍的，缩放操作的变换矩阵为：

$$T_s = \left(\begin{array}{cccc}s & 0 & 0 & 0 \\ 0 & s & 0 & 0 \\ 0 & 0 & s & 0 \\ 0 & 0 & 0 & 1\end{array}\right)$$

3.3 平移

所谓平移，就是在坐标系中的三个坐标轴保持不变，原点沿着平移向量移动到新位置。假设平移向量为$v_p = (\begin{array}{cccc}x_p & y_p & z_p & 0 \end{array})$同样，根据可以得到，平移操作的变换矩阵为：

$$T_p = \left(\begin{array}{cccc}1 & 0 & 0 & x_p \\ 0 & 1 & 0 & y_p \\ 0 & 0 & 1 & z_p \\ 0 & 0 & 0 & 1\end{array}\right)$$

3.4 旋转

最后来推导最难的旋转变换矩阵。与平移、旋转矩阵的不同，旋转矩阵就不那么直观了。下面，我们来具体看一下旋转矩阵的推导，这个推导是执行三次向量的平行四边形法则进行分解得到，整个分解过程如下图所示：

三次分解由不同的颜色表示出来了，分别是红色、浅蓝色和紫色。

已知条件：$\mathbf{i}$、$\mathbf{j}$和$\mathbf{k}$是三维笛卡尔坐标系的基向量，原点为$O$，旋转轴为$\mathbf{u}$，也是单位向量，向量$\mathbf{i'}$为$x$方向的基向量$\mathbf{i}$绕旋转轴$\mathbf{u}$旋转$\theta$后的新向量——旋转后坐标系$x$轴的基向量。

我们的目的：将向量$\mathbf{i'}$用基向量$\mathbf{i}$、$\mathbf{j}$和$\mathbf{k}$表示出来。

第一步向量分解：将$\mathbf{i'}$分解为沿着旋转轴$\mathbf{u}$的向量$\vec{OA}$和垂直于$\mathbf{u}$的向量$\vec{OB}$，则：

\begin{equation}\label{341}\mathbf{i'} = \vec{OA} + \vec{OB}\end{equation}

且：

\begin{equation}\label{342}\vec{OA} = u_x \mathbf{u} = u_x^2\mathbf{i} + u_xu_y\mathbf{j} + u_xu_z\mathbf{k}\end{equation}

第二步向量分解：将$\mathbf{i}$分解为沿着旋转轴$\mathbf{u}$的向量$\vec{OA}$和垂直于$\mathbf{u}$的向量$\vec{OC}$，则

$$\mathbf{i} = \vec{OA} + \vec{OC}$$

且：

\begin{equation}\label{344}\vec{OC} = \mathbf{i} - u_x\mathbf{u} = (1-u_x^2)\mathbf{i} - u_xu_y\mathbf{j} - u_xu_z\mathbf{k} \end{equation}

第三步向量分解：建立$\vec{OB}$与$\vec{OC}$之间的联系，将向量$\vec{OB}$分解为沿着$\vec{OC}$方向的向量$\vec{OD}$和垂直于$\vec{OB}$的向量$\vec{OE}$，则

\begin{equation}\label{345}\vec{OB} = \vec{OD} + \vec{OE}\end{equation}

根据$\ref{344}$可得：

\begin{equation}\label{346}\vec{OD} = |\vec{OB}|\cos\theta\frac{\vec{OC}}{|\vec{OC}|} = \cos\theta \vec{OC} = \cos\theta(\mathbf{i} - u_x\mathbf{u}) = (1-u_x^2)\cos\theta \mathbf{i} - u_xu_y\cos\theta \mathbf{j} -u_xu_z\cos\theta \mathbf{k} \end{equation}

另外，注意到$\vec{OE}$和$\vec{OC}$垂直，$\mathbf{u}$是旋转轴，则$\mathbf{u}$与平面$OEBD$垂直，所以$\mathbf{u}$与$OE$垂直，则$\vec{OE}$在向量$\mathbf{u}$和向量$\vec{OC}$的叉乘向量上，假设 $\vec{OF} = \mathbf{u} \times \vec{OC}$，于是：

$$\vec{OE} = k\vec{OF} = k\mathbf{u}\times \vec{OC}=k\mathbf{u}\times (\mathbf{i} - u_x\mathbf{u}) = k \mathbf{u}\times \mathbf{i}$$

所以现在求出$k$就可以了，由叉乘定义：$|\vec{OF}| = |\mathbf{u}||\vec{OC}|sin(90) = |\vec{OC}| = |\vec{OB}|$，所以：$k=\sin\theta$，最后得到

\begin{equation}\label{349}\vec{OE}=\sin\theta \mathbf{u}\times (\mathbf{i} - u_x\mathbf{u}) = \sin\theta \left(\begin{array} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ u_x & u_y & u_z \\ 1 & 0 & 0 \end{array}\right) =  u_z\sin\theta\mathbf{j} -u_y\sin\theta\mathbf{k}\end{equation}

将$(\ref{346})$和$(\ref{349})$代入$(\ref{345})$得：

\begin{equation}\label{3410}\vec{OB} = (1-u_x^2)\cos\theta\mathbf{i} - (u_xu_y\cos\theta - u_z\sin\theta)\mathbf{j} - (u_xu_z\cos\theta + u_y\sin\theta)\mathbf{k} \end{equation}

最后，将$(\ref{342})$和$(\ref{3410})$代入$(\ref{341})$可得

$$\mathbf{i'} = (\cos\theta + u_x^2(1-\cos\theta))\mathbf{i} + (u_xu_y(1-cos\theta) + u_z\sin\theta)\mathbf{j} + (u_xu_z(1-\cos\theta) - u_y\sin\theta)\mathbf{k} + 0\mathbf{O}$$

其余两个变换后的基向量$\mathbf{i'}$和$\mathbf{j'}$也可以由$\mathbf{i}$、$\mathbf{j}$和$\mathbf{k}$表示出来，最终得到齐次旋转矩阵为

$$M_r = \left(\begin{array}{cccc}\cos\theta+u_x^2(1-\cos\theta)& u_xu_y(1-\cos\theta)-u_z\sin\theta & u_xu_z(1-\cos\theta+u_y\sin\theta & 0 \\ u_yu_x(1-\cos\theta)+u_z\sin\theta & \cos\theta+u_y^2(1-\cos\theta) & u_yu_z(1-\cos\theta)-u_x\sin\theta & 0 \\ u_zu_x(1-\cos\theta)-u_y\sin\theta & u_zu_y(1-\cos\theta)+u_x\sin\theta & \cos\theta+u_z^2(1-\cos\theta) & 0 \\ 0 & 0 & 0 & 1\end{array}\right)$$

4 总结

最后总结一下，在这篇博文中我们讲述了点及其相对性，接着介绍了向量的概念，由平行四边形法则引出坐标系的概念，然后介绍了点在坐标系下的表示，最后介绍了坐标变换和变换矩阵的概念，给出了三种基本变换——平移变换、旋转变换和缩放变换的变换矩阵。这些矩阵综合运用，就构成了三维空间中复杂的变换了，三维变换是三维图形绘制的基础，也是学习OpenGL时较难理解的知识点之一。