简单RNN

递归神经网络（RNN）对于自然语言处理和其他序列任务非常有效，因为它们具有“记忆”功能。 它们可以一次读取一个输入x⟨t⟩

（如单词），并且通过隐藏层激活从一个时间步传递到下一个时间步来记住一些信息/上下文，这允许单向RNN从过去获取信息来处理后面的输入，双向RNN可以从过去和未来中获取上下文。

有些东西需要声明：

 

 

1 - 循环神经网络的前向传播
 我们来看一下下面的循环神经网络的图，在这里使用的是Tx=Ty，我们来实现它。

 

我们怎么才能实现它呢？有以下步骤：

实现RNN的一个时间步所需要计算的东西。
在Tx 时间步上实现一个循环，以便一次处理所有输入。

1.1 - RNN单元

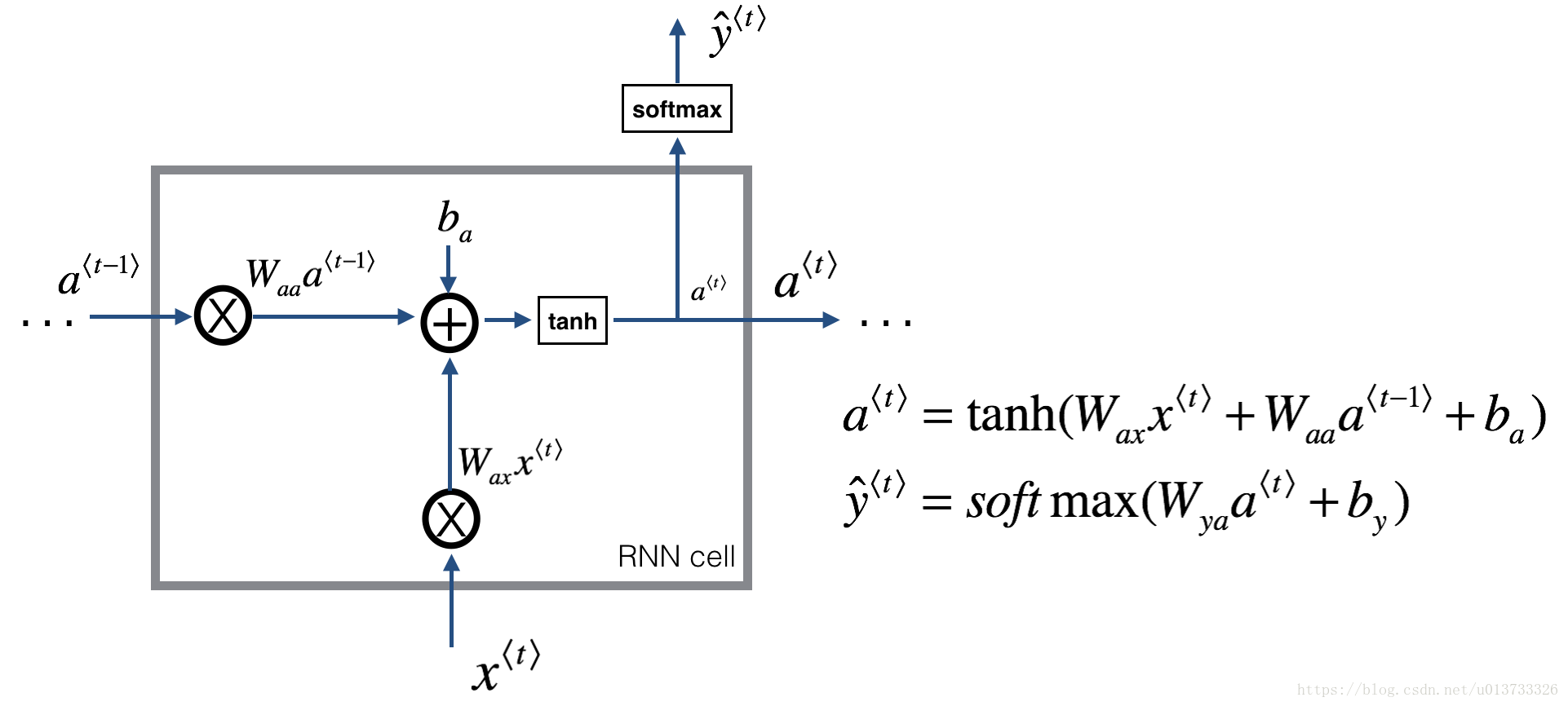
 循环神经网络可以看作是单元的重复，首先要实现单个时间步的计算，下图描述了RNN单元的单个时间步的操作。

 

def rnn_cell_forward(xt, a_prev, parameters):
    """
    根据图2实现RNN单元的单步前向传播
    
    参数：
        xt -- 时间步“t”输入的数据，维度为（n_x, m）
        a_prev -- 时间步“t - 1”的隐藏隐藏状态，维度为（n_a, m）
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）
    
    返回：
        a_next -- 下一个隐藏状态，维度为（n_a， m）
        yt_pred -- 在时间步“t”的预测，维度为（n_y， m）
        cache -- 反向传播需要的元组，包含了(a_next, a_prev, xt, parameters)
    """
    
    # 从“parameters”获取参数
    Wax = parameters["Wax"]
    Waa = parameters["Waa"]
    Wya = parameters["Wya"]
    ba = parameters["ba"]
    by = parameters["by"]
    
    # 使用上面的公式计算下一个激活值
    a_next = np.tanh(np.dot(Waa, a_prev) + np.dot(Wax, xt) + ba)
    
    # 使用上面的公式计算当前单元的输出
    yt_pred = rnn_utils.softmax(np.dot(Wya, a_next) + by)
    
    # 保存反向传播需要的值
    cache = (a_next, a_prev, xt, parameters)
    
    return a_next, yt_pred, cache

 

1.2 - RNN的前向传播

 可以看到的是RNN是刚刚构建的单元格的重复连接，如果输入的数据序列经过10个时间步，那么将复制RNN单元10次，每个单元将前一个单元中的隐藏状态

（a⟨t−1⟩ a^{\langle t-1 \rangle}a ⟨t−1⟩）和当前时间步的输入数据（x⟨t⟩ x^{\langle t \rangle}x ⟨t⟩）作为输入。 它为此时间步输出隐藏状态（a⟨t⟩ a^{\langle t \rangle}a ⟨t⟩）和预测（y⟨t⟩ y^{\langle t \rangle}y ⟨t⟩）。

我们要根据图3来实现前向传播的代码，它由以下几步构成：

创建0向量zeros(a)，它将保存RNN计算的所有的隐藏状态。

使用“a0 a_0a
0
​
”初始化“next”隐藏状态。

循环所有时间步：

使用rnn_cell_forward函数来更新“next”隐藏状态与cache。

使用a来保存“next”隐藏状态（第t）个位置。

使用y来保存预测值。

把cache保存到“caches”列表中。

返回a,y与caches。

def rnn_forward(x, a0, parameters):
    """
    根据图3来实现循环神经网络的前向传播
    
    参数：
        x -- 输入的全部数据，维度为(n_x, m, T_x)
        a0 -- 初始化隐藏状态，维度为 (n_a, m)
        parameters -- 字典，包含了以下内容:
                        Wax -- 矩阵，输入乘以权重，维度为（n_a, n_x）
                        Waa -- 矩阵，隐藏状态乘以权重，维度为（n_a, n_a）
                        Wya -- 矩阵，隐藏状态与输出相关的权重矩阵，维度为（n_y, n_a）
                        ba  -- 偏置，维度为（n_a, 1）
                        by  -- 偏置，隐藏状态与输出相关的偏置，维度为（n_y, 1）
    
    返回：
        a -- 所有时间步的隐藏状态，维度为(n_a, m, T_x)
        y_pred -- 所有时间步的预测，维度为(n_y, m, T_x)
        caches -- 为反向传播的保存的元组，维度为（【列表类型】cache, x)）
    """
    
    # 初始化“caches”，它将以列表类型包含所有的cache
    caches = []
    
    # 获取 x 与 Wya 的维度信息
    n_x, m, T_x = x.shape
    n_y, n_a = parameters["Wya"].shape
    
    # 使用0来初始化“a” 与“y”
    a = np.zeros([n_a, m, T_x])
    y_pred = np.zeros([n_y, m, T_x])
    
    # 初始化“next”
    a_next = a0
    
    # 遍历所有时间步
    for t in range(T_x):
        ## 1.使用rnn_cell_forward函数来更新“next”隐藏状态与cache。
        a_next, yt_pred, cache = rnn_cell_forward(x[:, :, t], a_next, parameters)
        
        ## 2.使用 a 来保存“next”隐藏状态（第 t ）个位置。
        a[:, :, t] = a_next
        
        ## 3.使用 y 来保存预测值。
        y_pred[:, :, t] = yt_pred
        
        ## 4.把cache保存到“caches”列表中。
        caches.append(cache)
    
    # 保存反向传播所需要的参数
    caches = (caches, x)
    
    return a, y_pred, caches