交叉熵损失函数

交叉熵损失是分类任务中的常用损失函数，但是是否注意到二分类与多分类情况下的交叉熵形式上的不同呢？

两种形式

这两个都是交叉熵损失函数，但是看起来长的却有天壤之别。为什么同是交叉熵损失函数，长的却不一样？

因为这两个交叉熵损失函数对应不同的最后一层的输出：
第一个对应的最后一层是softmax，第二个对应的最后一层是sigmoid

先来看下信息论中交叉熵的形式

 

 

 

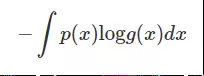
交叉熵是用来描述两个分布的距离的，神经网络训练的目的就是使 g(x) 逼近 p(x)。

 

softmax层的交叉熵

(x)是什么呢？就是最后一层的输出 y 。
p(x)是什么呢？就是我们的one-hot标签。我们带入交叉熵的定义中算一下，就会得到第一个式子：

其中 j 代表样本 x 属于第 j 类。

 

sigmoid作为输出的交叉熵

sigmoid作为最后一层输出的话，那就不能吧最后一层的输出看作成一个分布了，因为加起来不为1。

现在应该将最后一层的每个神经元看作一个分布，对应的 target 属于二项分布(target的值代表是这个类的概率)，那么第 i 个神经元交叉熵为：

 

 

所以最后一层总的交叉熵损失函数是：

 

 

 

但是在二分类中，逻辑回归的交叉熵损失函数同样具有两种形式，其原因是由类别取值所导致的。

1. 类别取值为0和1

   1. 逻辑回归中我们给定的假设函数（目标函数）是给定x的条件下，预测其属于类别1的概率，线性回归中的目标函数是：

      
      
       

      

       
      
      

      其中z是一个实数值，显然不能直接作为逻辑分类的预测值，因此想办法将其映射为概率值，引入了sigmoid函数，那么逻辑回归的假设函数就是：

      
      
       

      

       

   2. 有了假设函数，我们先尝试借鉴线性回归的方式定义损失函数：

      
      
       

      

       
      
      

      但是发现这样的损失函数并不是一个严格的凸函数，容易陷入局部最优解，因此摒弃该损失函数。
      由于我们引入的sigmoid可视作是类别为1的后验概率（说白了，就是给一个x，那么可以通过sigmoid算出来该样本点属于类别1的概率），所以可以得到类别为1以及类别为0时的条件概率为：

      
      
       

      

       
      
      上面两式合并在一起：
      
       

      

       

   3. MLE
      ok，现在我们得到了逻辑回归的分布函数（即最终的目标函数），那么我们现在为了唯一确定最优的模型，需要对模型中的参数进行估计。引入极大似然估计法，回忆一下MLE的目标，就是通过极大化已出现样本的联合概率来求解出我们认为最优的参数。
      根据极大似然法以及联合概率求解，得到：

      
      
       

      

       
      
      

      为了简化运算，我们对上面这个等式的两边取对数：

      
      
       

      

       
      
      目标就是找到使得上式最大的参数w，没错，对上式加上负号，就得到了逻辑回归的代价函数：
      
       

      

   类别为 1 和 -1 的情况

   首先回忆sigmoid的特殊性质：

   
   

    

   

    

   
   

   如果 y = +1 时

   
   

    

   

    

   
   如果 y = -1 时：
   

    

   

    

   
   

   因为 y 取值为 +1 或 -1，可以把 y 值带入，将上面两个式子整合到一起：

   
   

    

   

    

   
   

    

   

    

   
   引入MLE：
   

    

   

    

   
   

    

   

    

   
   将sigmoid形式代入：
   

    

   

    

   
   那么就推导出该情况下的交叉熵的损失函数形式了。
   

   如果有N个样本，那么：