完全背包问题

分析

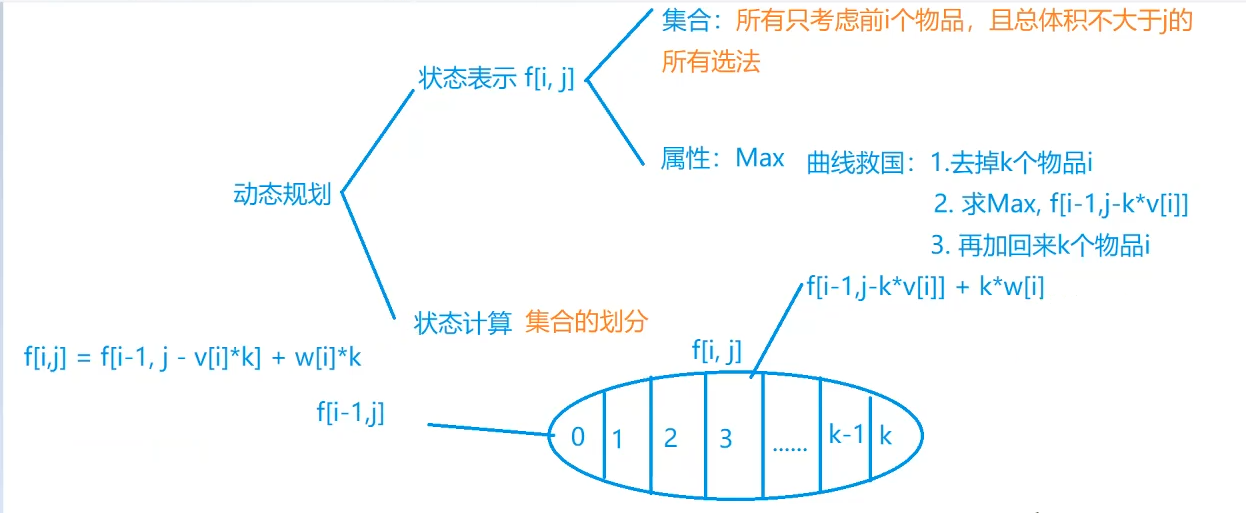
代码

朴素O(n^3)会TLE

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N];
int f[N][N];

int main(){
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
	
	for (int i = 1; i <= n; i ++ )
		for (int j = 0; j <= m; j ++ )
		for (int k = 0; k*v[i] <= j; k ++ )
	 		f[i][j] = max(f[i][j],f[i - 1][j - v[i]*k] + k*w[i]);
			
	cout << f[n][m] << endl;
	
    return 0;
}

O(n^2)优化代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N];
int f[N][N];

int main(){
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
	
	for (int i = 1; i <= n; i ++ )
		for (int j = 0; j <= m; j ++ )
		{
			f[i][j] = f[i-1][j];
			if (j >= v[i])
			f[i][j] = max(f[i][j],f[i][j-v[i]] + w[i]);
		}
		
	cout << f[n][m] << endl;
	
    return 0;
}

优化成一维数组形式

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>

using namespace std;

const int N = 1010;

int n,m;
int v[N],w[N];
int f[N];

int main(){
	scanf("%d%d",&n,&m);
	for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];
	
	for (int i = 1; i <= n; i ++ )
		for (int j = v[i]; j <= m; j ++ )
			f[j] = max(f[j],f[j-v[i]] + w[i]);
		
	cout << f[m] << endl;
	
    return 0;
}

01背包与完全背包状态转移方程异同：

为什么会有这样的差异？