下推自动机(PDA)在程序设计中的应用
(一)下推自动机简介(Pushdown Automation)
下推自动机﹙PDA﹚是自动机理论中定义的一种抽象的计算模型。下推自动机比有限状态自动机复杂:除了有限状态组成部分外,还包括一个长度不受限制的栈;下推自动机的状态迁移不但要参考有限状态部分,也要参照栈当前的状态;状态迁移不但包括有限状态的变迁,还包括一个栈的出栈或入栈过程。
物理模型如下:
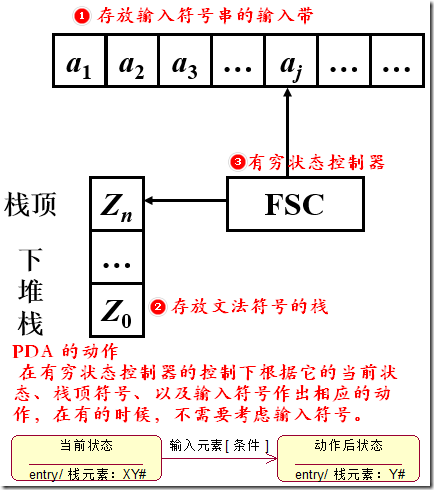
PDA 应该含有三个基本结构:①存放输入符号串的输入带 ②存放文法符号的栈 ③有穷状态控制器。
PDA的动作:在有穷状态控制器的控制下根据它的当前状态、栈顶符号、以及输入符号作出相应的动作,在有的时候,不需要考虑输入符号。
(二)PDA的形式语言定义
下推自动机 (pushdown automaton,PDA) M = (Q, ∑, Γ, δ, q0 , Z0 , F)
Q——状态的非空有穷集合。q∈Q,q 称为M 的一个状态(state);
∑——输入字母表 (input alphabet)。要求 M 的输入字符串都是∑上的字符串;
Γ——栈符号表 (stack alphabet)。∀A∈Γ,叫做一个栈符号;
Z0——Z0∈Γ叫做开始符号(start symbol),是 M 启动时候栈内惟一的一个符号。所以,习惯地称其为栈底符号;
q0——q0∈Q,是 M 的开始状态(initial state),也可叫做初始状态或者启动状态;
F——FQ,是 M 的终止状态(final state) 集合,简称为终态集。∀q∈F,q 称为 M 的终止状态,也可称为接受状态 (accept state),简称为终态。
δ——状态转移函数(transition function),有时候又叫做状态转换函数或者移动函数。 描述如下:
①:δ(q, a, Z )={ (p1, γ1) , (p2, γ2) , … , (pm, γm) } 表示 M 在状态 q,栈顶符号为 Z 时,读入字符 a,对于i = 1, 2, …, m,可以选择地将状态变成 pi,并将栈顶符号 Z 弹出,将 γi 中的符号从右到左依次压入栈,然后将读头向右移动一个带方格而指向输入字符串的下一个字符。
②:δ(q,ε, Z)={(p1, γ1), (p2, γ2),…,(pm, γm)} 表示 M 进行一次ε-移动 (空移动),即 M 在状态 q,栈顶符号为 Z 时,无论输入符号是什么,对于 i = 1, 2, …, m,可以选择地将状态变成 pi,并将栈顶符号 Z 弹出,将 γi 中的符号从右到左依次压入栈,读头不移动。



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:向量存储与相似性搜索在 .NET 中的实现
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· winform 绘制太阳,地球,月球 运作规律
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人