[题解]洛谷P3384 轻重链剖分
首先是传送门:洛谷P3384轻重链剖分
先把版面拿过来
题面
题目描述
如题,已知一棵包含 NN 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作 11: 格式: 1\ x\ y\ z1 x y z 表示将树从 xx 到 yy 结点最短路径上所有节点的值都加上 zz。
操作 22: 格式: 2\ x\ y2 x y 表示求树从 xx 到 yy 结点最短路径上所有节点的值之和。
操作 33: 格式: 3\ x\ z3 x z 表示将以 xx 为根节点的子树内所有节点值都加上 zz。
操作 44: 格式: 4\ x4 x 表示求以 xx 为根节点的子树内所有节点值之和
输入格式
第一行包含 44 个正整数 N,M,R,PN,M,R,P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 NN 个非负整数,分别依次表示各个节点上初始的数值。
接下来 N-1N−1 行每行包含两个整数 x,yx,y,表示点 xx 和点 yy 之间连有一条边(保证无环且连通)。
接下来 MM 行每行包含若干个正整数,每行表示一个操作,格式如下:
操作 11: 1\ x\ y\ z1 x y z;
操作 22: 2\ x\ y2 x y;
操作 33: 3\ x\ z3 x z;
操作 44: 4\ x4 x。
输出格式
输出包含若干行,分别依次表示每个操作 22 或操作 44 所得的结果(对 PP 取模)。
输入输出样例
5 5 2 24 7 3 7 8 0 1 2 1 5 3 1 4 1 3 4 2 3 2 2 4 5 1 5 1 3 2 1 3
2 21
说明/提示
数据规模:
对于 30\%30% 的数据: 1 \leq N \leq 10,1 \leq M \leq 101≤N≤10,1≤M≤10;
对于 70\%70% 的数据: 1 \leq N \leq {10}^3, 1 \leq M \leq {10}^31≤N≤103,1≤M≤103;
对于 100\%100% 的数据: 1\le N \leq {10}^5, 1\le M \leq {10}^5,1\le R\le N,1\le P \le 2^{31}-11≤N≤105,1≤M≤105,1≤R≤N,1≤P≤231−1。
样例说明:
树的结构如下:
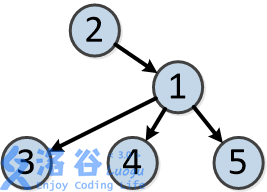
各个操作如下:
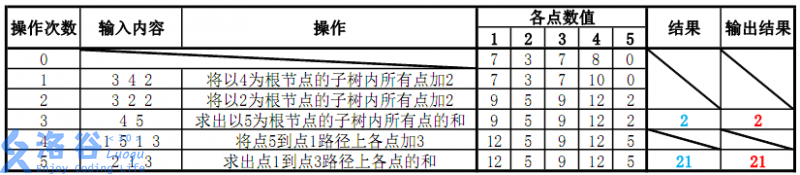
故输出应依次为 22 和 2121。
分析
首先我们很容易看出这是一道树链剖分的模板题。
先建边,再建线段树,通过线段树区间维护来维护这颗树。
在树链剖分时由于先遍历重边,所以新编号中重边是连续的。
同时新编号子树的排列也是连续的,所以可以通过线段树维护。
因为是模板题所以不用讲太多了。
代码贴出来
#include<iostream> #include<fstream> using namespace std; const int Max_N = 4e5 + 5; typedef long long ll; #define lson(x) (x<<1) #define rson(x) (x<<1|1) int n,m,r,p; ll A[Max_N]; int cnt; int head[Max_N],nxt[Max_N],to[Max_N]; ll w[Max_N],s[Max_N]; int tot; int tag[Max_N],No[Max_N],size[Max_N],Fa[Max_N],heavy[Max_N],top[Max_N],dep[Max_N]; inline void Add_Edge(int,int,ll); inline void dfs1(int); inline void dfs2(int,int); inline void Add_line(int,int,ll); inline ll Query_line(int,int); inline void Add_tree(int,ll); inline ll Query_tree(int); inline void build(int,int,int); inline void modify(int,ll,int,int,int,int); inline void update_w(int); inline void down(int,int,int); inline ll Query(int,int,int,int,int); int main() { scanf("%d%d%d%d",&n,&m,&r,&p); int i; for(i = 1;i <= n;i++) scanf("%lld",&A[i]); int x,y; for(i = 1;i < n;i++){ scanf("%d%d",&x,&y); Add_Edge(x,y,A[i]); Add_Edge(y,x,A[i]); } dfs1(r); dfs2(r,r); build(1,1,tot); int opi,z; for(i = 1;i <= m;i++){ scanf("%d",&opi); switch(opi){ case 1: scanf("%d%d%lld",&x,&y,&z); Add_line(x,y,z); break; case 2: scanf("%d%d",&x,&y); printf("%lld\n",Query_line(x,y)); break; case 3: scanf("%d%lld",&x,&z); Add_tree(x,z); break; case 4: scanf("%d",&x); printf("%lld\n",Query_tree(x)); break; } } return 0; } inline void Add_Edge(int x,int y,ll k) { to[++cnt] = y; nxt[cnt] = head[x]; head[x] = cnt; return ; } inline ll Query_tree(int x) { return Query(1,No[x],No[x] + size[x] - 1,1,n) % p; } inline void Add_tree(int x,ll k) { modify(1,k,No[x],No[x] + size[x] - 1,1,n); return ; } inline void Add_line(int x,int y,ll k) { while(top[x] != top[y]){ if(dep[top[x]] < dep[top[y]]) swap(x,y); modify(1,k,No[top[x]],No[x],1,tot); x = Fa[top[x]]; } if(dep[x] > dep[y]) swap(x,y); modify(1,k,No[x],No[y],1,tot); return ; } inline ll Query(int idx,int x,int y,int l,int r) { if(l > y || r < x) return (ll)0; if(x <= l && r <= y) return s[idx]; down(idx,l,r); int mid = l + r >> 1; return (Query(lson(idx),x,y,l,mid) % p + Query(rson(idx),x,y,mid+1,r) % p ) % p; } inline ll Query_line(int x,int y) { ll res = 0; while(top[x] != top[y]){ if(dep[top[x]] < dep[top[y]]) swap(x,y); res += Query(1,No[top[x]],No[x],1,tot); x = Fa[top[x]]; } if(dep[x] > dep[y]) swap(x,y); return (res % p + Query(1,No[x],No[y],1,tot) % p) % p; } inline void down(int idx,int l,int r) { if(tag[idx]){ int mid = l + r >> 1; s[lson(idx)] += tag[idx] * (mid - l + 1); s[lson(idx)] = s[lson(idx)] % p; s[rson(idx)] += tag[idx] * (r - mid); s[rson(idx)] = s[rson(idx)] % p; tag[lson(idx)] += tag[idx]; tag[rson(idx)] += tag[idx]; tag[idx] = 0; } return ; } inline void update_w(int idx) { s[idx] = ((s[lson(idx)] % p) + (s[rson(idx)] % p)) % p; return ; } inline void modify(int idx,ll k,int x,int y,int l,int r) { if(l > y || r < x) return ; if(x <= l && r <= y){ s[idx] = ((s[idx] % p) + ((r - l + 1) * k)%p)%p; tag[idx] += k%p; return ; } down(idx,l,r); int mid = l + r >> 1; modify(lson(idx),k,x,y,l,mid); modify(rson(idx),k,x,y,mid + 1,r); update_w(idx); return ; } inline void dfs1(int idx) { size[idx] = 1; dep[idx] = dep[Fa[idx]] + 1; int i; for(i = head[idx];i;i = nxt[i]){ if(to[i] == Fa[idx]) continue; Fa[to[i]] = idx; dfs1(to[i]); size[idx] += size[to[i]]; if(!heavy[idx] || size[heavy[idx]] < size[to[i]]) heavy[idx] = to[i]; } return ; } inline void dfs2(int idx,int t) { No[idx] = ++tot; w[tot] = A[idx] % p; top[idx] = t; if(heavy[idx]) dfs2(heavy[idx],t); int i; for(i = head[idx];i;i = nxt[i]){ if(to[i] == Fa[idx] || to[i] == heavy[idx]) continue; dfs2(to[i],to[i]); } return ; } inline void build(int idx,int l,int r) { if(l == r){ s[idx] = w[l]%p; return ; } int mid = l + r >> 1; build(lson(idx),l,mid); build(rson(idx),mid + 1,r); update_w(idx); return ; }


