[题解]图的遍历
版权说明:来自洛谷P3916
题目描述
给出$N$个点,$M$条边的有向图,对于每个点$v$,求$A(v)$表示从点$v$出发,能到达的编号最大的点。
输入输出格式:
输入格式:
第1 行,2 个整数$N,M$。
接下来$M$行,每行2个整数$U_i,V_i$,表示边$(U_i,V_i)$。点用$1, 2,\cdots,N$编号。
输出格式:
N 个整数$A(1),A(2),\cdots,A(N)$。
说明
• 对于60% 的数据,$1 \le N . K \le 10^3$;
• 对于100% 的数据,$1 \le N , M \le 10^5$。
思路:
首先在没有处理前是有向有环图,这样我们直接DFS是会超时的(当然据说还有 DFS100次 玄学做法,但是不推荐)。我们通过tarjan缩点后将其变为有向无环图,如图
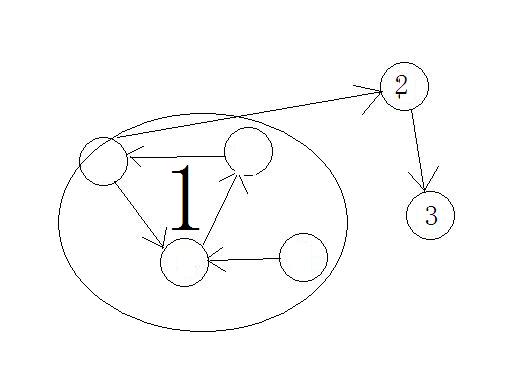
那么后面的事情就很简单了,我们首先染色,继承边,再通过DFS得到结果。当然你也可以记忆化让时间跑快一点。具体请看代码
代码:

1 #include<iostream> 2 #include<fstream> 3 #include<cstring> 4 #include<stack> 5 using namespace std; 6 const int Max_N=1e5+5; 7 const int Max_E=1e5+5; 8 9 int n,e; 10 int U[Max_E],V[Max_E],rem[Max_N]; 11 12 int tot; 13 int head[Max_N],Next[Max_E],to[Max_E]; 14 15 int Index; 16 stack<int>sta; 17 int DFN[Max_N],LOW[Max_N]; 18 bool vis[Max_N]; 19 20 int cnt; 21 int PoiV[Max_N],PoiP[Max_N]; 22 23 void Add_Edge(int u,int v) 24 { 25 Next[++tot]=head[u]; 26 head[u]=tot; 27 to[tot]=v; 28 // 前向星 29 return ; 30 } 31 void tarjan(int p) 32 { 33 vis[p]=1; 34 sta.push(p); 35 DFN[p]=LOW[p]=++Index; 36 register int i; 37 for(i=head[p];i^0;i=Next[i]){ 38 int u=p,v=to[i]; 39 if(!DFN[v]){ 40 tarjan(v); 41 LOW[u]=min(LOW[u],LOW[v]); 42 } 43 else if(vis[v]) 44 LOW[u]=min(LOW[u],DFN[v]); 45 } 46 // tarjan操作 47 if(DFN[p]==LOW[p]){ 48 int pos; 49 cnt++; 50 while(pos=sta.top()){ 51 sta.pop(); 52 vis[pos]=0; 53 PoiP[pos]=cnt; 54 PoiV[cnt]=max(PoiV[cnt],pos); 55 // 染色 56 if(pos==p) 57 break; 58 } 59 } 60 return ; 61 } 62 int DFS(int p) 63 { 64 if(rem[p]^-1) 65 return rem[p]; 66 rem[p]=PoiV[p]; 67 register int i; 68 for(i=head[i];i^0;i=Next[i]) 69 rem[p]=max(rem[p],DFS(to[i])); 70 // 记忆化搜索得到答案 71 return rem[p]; 72 } 73 int main() 74 { 75 scanf("%d%d",&n,&e); 76 register int i,j; 77 for(i=1;i<=e;i++){ 78 scanf("%d%d",&U[i],&V[i]); 79 Add_Edge(U[i],V[i]); 80 } 81 for(i=1;i<=n;i++) 82 if(!DFN[i]) 83 tarjan(i); 84 // tarjan 85 tot=0; 86 memset(head,0,sizeof(head)); 87 // 清空边 88 for(i=1;i<=e;i++) 89 if(PoiP[U[i]]^PoiP[V[i]]) 90 Add_Edge(PoiP[U[i]],PoiP[V[i]]); 91 // 这里好好理解,继承边部分 92 memset(rem,-1,sizeof(rem)); 93 for(i=1;i<=cnt;i++) 94 DFS(i); 95 // 求出缩点后边的答案 96 for(i=1;i<=n;i++){ 97 if(i>1) 98 printf(" "); 99 printf("%d",rem[PoiP[i]]); 100 } 101 // 输出 102 return 0; 103 }


