
转载请注明 https://www.cnblogs.com/lihaqwq/p/9501876.html
1.对曲线曲面积分的理解
第一型曲线积分和第一型曲面积分是以线密度和面密度为背景的线积分,强调是以线段(弧长)、面积为积分
元素即:ds
第二型曲线曲面积分则是分别以力做功和流量为背景的积分,强调的是对坐标的积分。实际上我认为第二类曲
线曲面积分就是对矢量进行积分的一种积分规则。二、三维空间的矢量依靠分解到三个坐标轴上分别
积分,其中需要通过变换积分元素 、
、 。
。
所以进行计算时按第一类曲线曲面和第二类曲线曲面积分进行区分计算思维上来得更直接。比如第一型曲线曲
面积分是线密度和面密度的基础上来的自然没有方向问题。而第二型曲线曲面积分是做功与流量的矢量计算自然
有方向、又先后。同样第一型曲线曲面积分只需要变化积分元素和变量,而第二型积分是矢量的点乘基础上推导
而来,自然就涉及到偏导数、方向导数以及梯度。
2.第一型曲线曲面积分
第一型曲线积分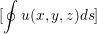 :只需要将ds变为dx即可
:只需要将ds变为dx即可
第一型曲面积分 :同样只需要将ds化为dx同时投影到那个面将对应的变量当成因变量进行
:同样只需要将ds化为dx同时投影到那个面将对应的变量当成因变量进行
改写。(这里的ds指的是面积元素)
tip 1:第一型曲面积分的计算中,若出现封闭曲面需要切割成多个面,直到投影不重合。例如
 就需要分解成2个曲面。
就需要分解成2个曲面。
3.第二型曲线积分
第二型曲线积分又叫对坐标的线积分。按照物理意义进行解释就是力和路程被分解到二维、三维的坐标轴上
直观的进行分析。但是计算的时候需要化到一个坐标轴上进行计算,或者格林公式等手段。
3.1格林公式
![]() 满足单连通和双联通,P、Q一阶连续可偏即可。
满足单连通和双联通,P、Q一阶连续可偏即可。
tip:格林公式实际上就是把线积分化成了二重积分进行计算,所以在为了简化运算进行替换时注意分清楚阶段。
是线积分的限制条件只能在线积分内进行替换。包括积分域的等量代换,积分域对称的奇偶变化。
3.2与路径无关(什么叫柯西黎曼可积:我不是 我没有 别问我。有兴趣自己找一下证明流程)
当第二型先积分满足:1:积分域单连通(单单单单连通!!!) 2:P、Q一阶连续可偏导
并满足![]() ,就称积分与路径无关。
,就称积分与路径无关。
一般与路径无关有2种计算方法:1:既然与路径无关,找与坐标轴平行的路径以避开dx或者dy的积分。
2:满足与路径无关的第三个条件恰好是全微分的特征,找到原函数即可。经过实践,此
方法与计算不太搭调,多用来证明或者求原函数,与微分方程联系。
tips 1:能用与路径无关就能用格林公式![]() ,偏偏两个偏导数相等。一般能出现下面的情况
,偏偏两个偏导数相等。一般能出现下面的情况
求曲线积分![]() ,l曲线没有经过无定义点的闭曲线。这个时候用格林公式方便快捷。也可以直接使
,l曲线没有经过无定义点的闭曲线。这个时候用格林公式方便快捷。也可以直接使
用结论沿G内任意闭曲线的曲线积分为零。
2:与格林类似包括曲面积分,在为了简化运算进行替换时注意分清楚阶段,上一阶段的限制条件不能拿到下一阶段使用。
同一阶段对积分域有多个限制条件也不能以偏概全的代替。
4.第二型曲面积分(想想高中时代学过的力的分解瞬间ez)
4.1计算方法
按照方法的特点上来讲我习惯叫做二重积分法和三重积分法,直接法就是化到3个坐标平面直接积分。高斯公式就是化到三维空间
的体积分。(学过一遍再去看同济教材,才发现教材写得其实相当棒,特别是证明的连贯性)
tips 1:奇偶性有异,由于曲面上向量与坐标轴的夹角关系,关于坐标轴对称的面上对应点的方向余弦互为相反数,所以函数的
奇偶性在第二型曲面积分上的性质恰好相反。
2:同上注意替换的阶段性。同时注意到底哪个才是真的得积分域曲面,形成圆锥曲线的截面不是积分域,可以理解成自变
量的限制条件。
难度不大,把握细节,注意理解,加油
傻蛋 傻蛋 傻蛋 over




