石墨烯在两个重要方面与大多数光学材料不同。 首先，它通常是非常薄的材料层，厚度仅为一个原子。 其次，通常使用表面电导率而不是体积介电常数来表征。 FDTD和MODE中的石墨烯材料模型允许将石墨烯精确地模拟为2D材料，而无需非常小的网格，从而加快了模拟速度。最常用的就是表面电导率模型。
根据Kubo公式，表面电导率模型（单层石墨烯）：由带内电导率和带间电导率两部分组成
\[\sigma(\omega,\Gamma,\mu_c,T)=\sigma_{intra}(\omega,\Gamma,\mu_c,T)+\sigma_{inter}(\omega,\Gamma,\mu_c,T)
\]
\[\sigma_{intra}(\omega,\Gamma,\mu_c,T)=\frac{-ie^2}{\pi\hbar^2(\omega+i2\Gamma)}\int^{\infty}_0\xi(\frac{\partial f_d(\xi)}{\partial\xi}-\frac{\partial f_d(-\xi)}{\partial\xi})d\xi
\]
\[\sigma_{inter}(\omega,\Gamma,\mu_c,T)=\frac{-ie^2(\omega+i2\Gamma)}{\pi\hbar^2}\int^{\infty}_0\frac{f_d(-\xi)-f_d(\xi)}{(\omega+i2\Gamma)^2-4(\xi/\hbar)^2}d\xi
\]
其中：
\(\omega\):角频率，\(\Gamma\):散射率，\(\mu_c\):化学势,其大小由载流子浓度\(n_s决定\)，T：温度，e:元电荷或基本电量，\(\hbar\):约化普朗克常量，\(\kappa_B\):玻尔兹曼常量，以及：
\[f_d(\xi)=\frac{1}{exp((\xi-\mu_c)/(\kappa_BT))+1}
\]
为费米—狄拉克分布。FDTD中添加表面电导率模型：
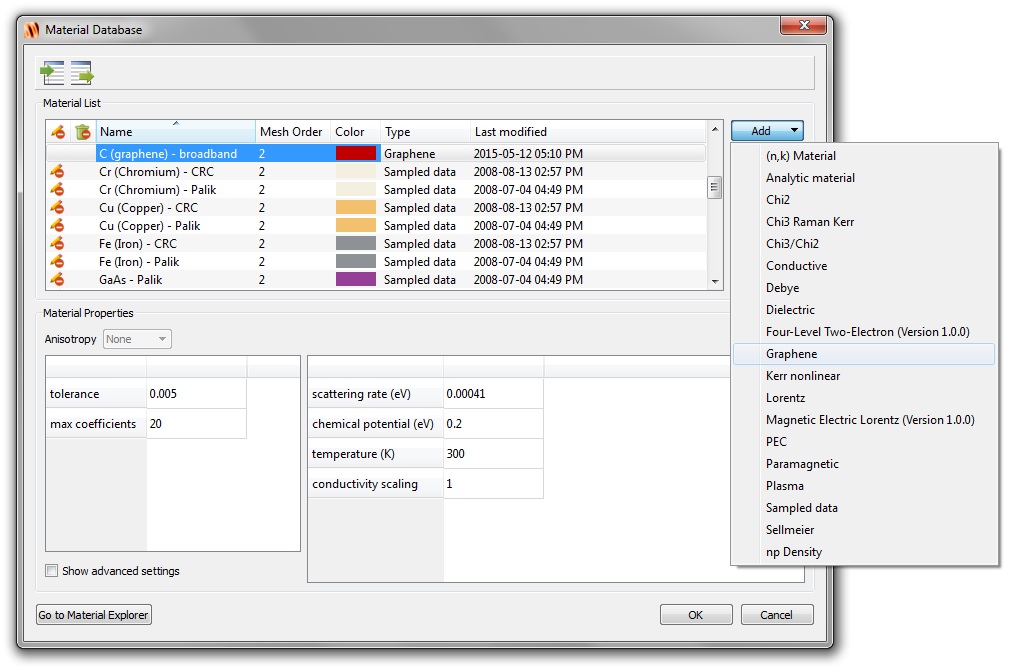
严格来说，由（1）-（4）公式指定的表面电导率材料模型仅对单个石墨烯层有效。 但是，在某些情况下，该模型也可以通过按层数缩放总电导率来表示多层。 为此，在石墨烯材料类型的材料参数中已包含了电导率比例因子（参见上图）。 比例因子乘以（2）和（3）。 一旦指定了所需的散射速率，化学势，温度和比例因子，就可以在材料浏览器中显示相应的表面电导率。将石墨烯材料类型的实例添加到材料数据库后，即可将其分配给任何2D矩形。这提供了将石墨烯层引入仿真的简单机制。为了生成石墨烯的表面电导率，石墨烯材料类型通过分析来评估带内电导率项和带间电导率项。 使用以下公式评估带内项：
\[\sigma_{intra}(\omega,\Gamma,\mu_c,T)=\frac{ie^2\kappa_BT}{\pi\hbar^2(\omega+i2\Gamma)}\left[\frac{\mu_c}{\kappa_BT}+2\ln\left(exp\left(-\frac{\mu_c}{\kappa_BT}\right)+1\right)\right]=\frac{ie^2\kappa_BT}{\pi\hbar^2(2\pi v\lambda^{-1}+i\tau^{-1})}\left[\frac{\mu_c}{\kappa_BT}+2\ln\left(exp\left(-\frac{\mu_c}{\kappa_BT}\right)+1\right)\right]
\]
\[\sigma_{inter}=\frac{ie^2}{4\pi\hbar}\ln\left[\frac{2|\mu_c|-(2\pi v\lambda^{-1}+i\tau^{-1})\hbar}{2|\mu_c|+(2\pi v\lambda^{-1}+i\tau^{-1})\hbar}\right]
\]
其中，\(v\)为光速，\(\lambda\)为响应波长，\(\mu\approx10^4 cm^2\cdot V^{-1}\cdot s^{-1}\)为电子迁移率，\(v_F\approx10^6m\cdot s^{-1}\)为费米速度,设x为化学势的值
\[\tau=\frac{1}{2\Gamma}=\frac{\mu\mu_c}{ev_F^2}=\frac{10^4\cdot cm^2\cdot V^{-1}\cdot S^{-1}\cdot (x)eV}{e\cdot m\cdot S^{-1}\cdot m\cdot S^{-1}\cdot 10^6\cdot 10^6}=x\cdot 10^{-12}S，\mu_c\approx\hbar v_f\sqrt{\pi n_s},\Gamma=\frac{1}{2\tau}=\frac{1}{2x}\cdot 10^{12}Hz=\frac{1}{2x}THz=\frac{1}{2x}\cdot 10^{12}\times4.1356676969\times10^{-15}\div2\pi eV
\]
当\(T=300K\)以及\(\kappa_BT<<|\mu_c|\)时，在太赫兹和中红外波段的带内电导率\(\sigma_{intra}\)起主导作用，石墨烯表面电导率可以简化为：
\[\sigma(\lambda)=\frac{ie^2\mu_c}{\pi\hbar^2(2\pi v\lambda^{-1}+i\tau^{-1})}，\sigma_N(\lambda)=N\sigma(\lambda)
\]
在数值模拟计算中，石墨烯可以被视为厚度为1nm的薄层，石墨烯在平面方向上的介电常数\(\varepsilon\)与复表面电导率\(\sigma(\lambda)\)之间的关系为：
\[\varepsilon=1+\frac{i\sigma(\lambda)}{\varepsilon_0 2\pi v\lambda^{-1}\Delta}
\]
式中，\(\Delta\)为石墨烯的厚度，\(\varepsilon_0\)为真空介电常数。
折射率灵敏度：
\[S=\frac{\Delta\lambda_{res}}{\Delta n}
\]
式中，\(\Delta\lambda_{res}\)为共振波长的变化量，\(\Delta n\)为折射率的变化量。
品质因数：
\[FOM=\frac{S}{FWHM}
\]
\(FWHM\)为共振谷的半峰全宽。
