8种排序算法
共分为五大类:交换排序(冒泡排序、快速排序);插入排序(直接插入排序、希尔排序);选择排序(简单选择排序、堆排序);归并排序;基数排序。
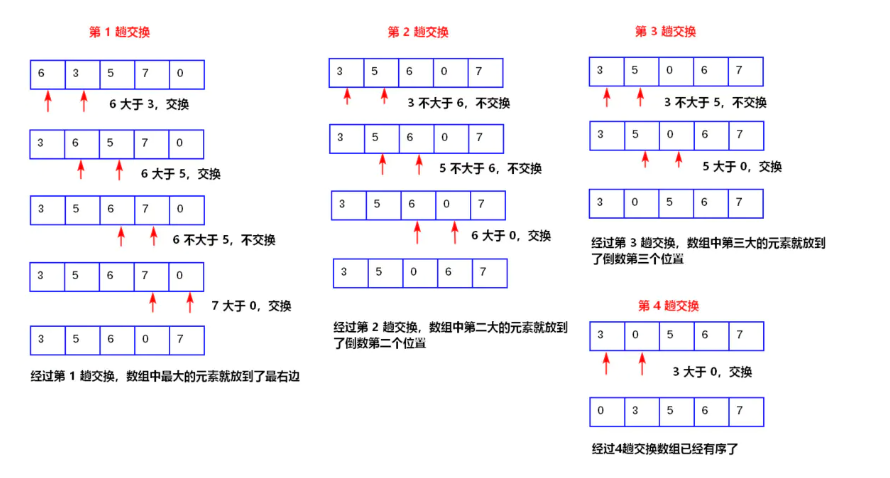
(1)冒泡排序:
比较两个相邻的元素,将值大的元素交换到右边
import java.util.Arrays;
public class BubbleSort {
public static void main(String[] args) {
int[] arr=new int[] {5,7,2,9,4,1,0,5,7};
System.out.println(Arrays.toString(arr));
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
//冒泡排序
/**
* 5,7,2,9,4,1,0,5,7 共需要比较length-1轮
* 5,7,2,9,4,1,0,5,7
* 5,2,7,9,4,1,0,5,7
* 5,2,7,4,1,0,5,7,9
* 2,5
*/
public static void bubbleSort(int[] arr) {
//控制共比较多少轮
for(int i=0;i<arr.length-1;i++) {
//控制比较的次数
for(int j=0;j<arr.length-1-i;j++) {
if(arr[j]>arr[j+1]) {
int temp=arr[j];
arr[j]=arr[j+1];
arr[j+1]=temp;
}
}
}
}
}
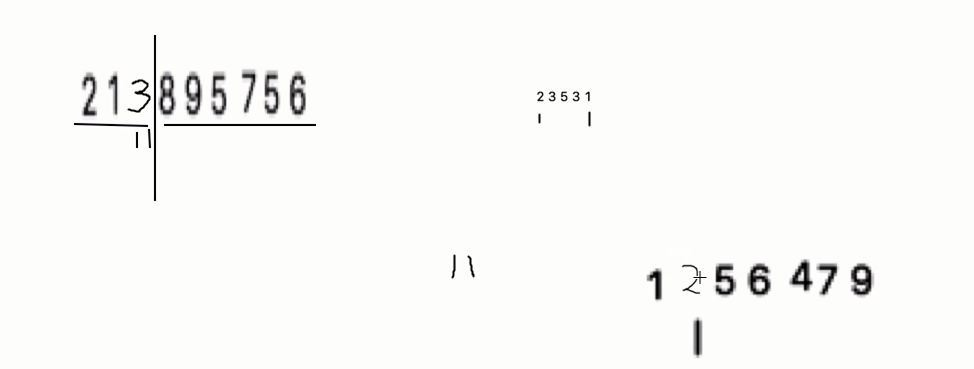
(2)快速排序,使用递归思想:
快速排序是对冒泡排序的一种改进。它的基本思想是:通过一次排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一不部分的所有数据都要小,然后再按次方法对这两部分数据分别进行快速排序,整个排序过程可以递归或者非递归进行,以此达到整个数据变成有序序列。
参考:https://www.sohu.com/a/246785807_684445
import java.util.Arrays;
public class QuickSort {
public static void main(String[] args) {
int[] arr = new int[] {3,4,6,7,2,7,2,8,0,9,1};
quickSort(arr,0,arr.length-1);
System.out.println(Arrays.toString(arr));
}
public static void quickSort(int[] arr,int start,int end) {
if(start<end) {
//把数组中的第0个数字做为标准数
int stard=arr[start];
//记录需要排序的下标
int low=start;
int high=end;
//循环找比标准数大的数和比标准数小的数
while(low<high) {
//右边的数字比标准数大
while(low<high&&stard<=arr[high]) {
high--;
}
//使用右边的数字替换左边的数
arr[low]=arr[high];
//如果左边的数字比标准数小
while(low<high&&arr[low]<=stard) {
low++;
}
arr[high]=arr[low];
}
//把标准数赋给低所在的位置的元素
arr[low]=stard;
//处理所有的小的数字
quickSort(arr, start, low);
//处理所有的大的数字
quickSort(arr, low+1, end);
}
}
}
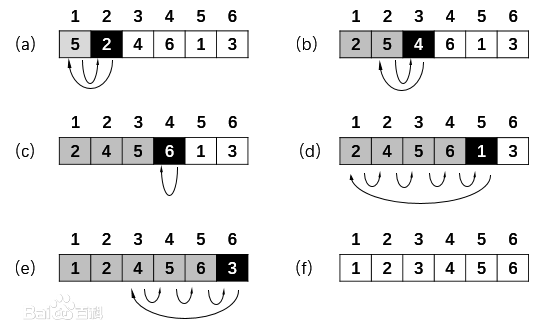
(3)直接插入排序:
将一个记录插入到已排好序的序列中,从而得到一个新的有序序列(将序列的第一个数据看成是一个有序的子序列,然后从第二个记录逐个向该有序的子序列进行有序的插入,直至整个序列有序)
参考:https://www.sohu.com/a/246785807_684445
import java.util.Arrays;
public class InsertSort {
public static void main(String[] args) {
int[] arr = new int[] {5,3,2,8,5,9,1,0};
insertSort(arr);
System.out.println(Arrays.toString(arr));
}
//插入排序
public static void insertSort(int[] arr) {
//遍历所有的数字
for(int i=1;i<arr.length;i++) {
//如果当前数字比前一个数字小(待排元素小于有序序列的最后一个元素时,向前插入)
if(arr[i]<arr[i-1]) {
//把当前遍历数字存起来
int temp=arr[i];
int j;
//遍历当前数字前面所有的数字
for(j=i-1;j>=0&&temp<arr[j];j--) {
//把前一个数字赋给后一个数字
arr[j+1]=arr[j];
}
//把临时变量(外层for循环的当前元素)赋给不满足条件的后一个元素
arr[j+1]=temp;
}
}
}
}

(4)希尔排序
参考:https://blog.csdn.net/qq_39207948/article/details/80006224
https://baijiahao.baidu.com/s?id=1644158198885715432&wfr=spider&for=pc
import java.util.Arrays;
public class ShellSort {
public static void main(String[] args) {
int[] arr = new int[] { 3, 5, 2, 7, 8, 1, 2, 0, 4, 7, 4, 3, 8 };
System.out.println(Arrays.toString(arr));
shellSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void shellSort(int[] arr) {
int k = 1;
// 遍历所有的步长
for (int d = arr.length / 2; d > 0; d /= 2) {
// 遍历该d下所有元素
for (int i = d; i < arr.length; i++) {
// 遍历本组中所有的元素(以d为间隔,...,i-2d,i-d,i,i+d,i+2d,...),由于i++,各组同时进行,d=1时,等同于做直接插入排序
for (int j = i - d; j >= 0; j -= d) {
// 如果当前元素大于加上步长后的那个元素
if (arr[j] > arr[j + d]) {
int temp = arr[j];
arr[j] = arr[j + d];
arr[j + d] = temp;
}
}
}
System.out.println("第" + k + "次排序结果:" + Arrays.toString(arr));
k++;
}
}
}
(5)直接选择排序:
选择排序法第一次扫描会找出最大或者最小值,放到正确的位置;第二次扫描会在剩余数据找出最大或者最小值,放到正确位置;以此类推,直到扫描完成。
步骤:1.从待排序序列中,找到最小的元素;
2.如果最小元素不是待排序序列的第一个元素,将其和第一个元素互换;
3.从余下的 N - 1 个元素中,找出关键字最小的元素,重复(1)、(2)步,直到排序结束。
参考:https://www.jianshu.com/p/f78295dcec07
import java.util.Arrays;
public class SelectSort {
public static void main(String[] args) {
int[] arr = new int[] {3,4,5,7,1,2,0,3,6,8};
selectSort(arr);
System.out.println(Arrays.toString(arr));
}
//选择排序
public static void selectSort(int[] arr) {
//遍历所有的数
for(int i=0;i<arr.length;i++) {
int minIndex=i;
//把当前遍历的数和后面所有的数依次进行比较,并记录下最小的数的下标
for(int j=i+1;j<arr.length;j++) {
//如果后面比较的数比记录的最小的数小。
if(arr[minIndex]>arr[j]) {
//记录下最小的那个数的下标
minIndex=j;
}
}
//如果最小的数和当前遍历数的下标不一致,说明下标为minIndex的数比当前遍历的数更小。
if(i!=minIndex) {
int temp=arr[i];
arr[i]=arr[minIndex];
arr[minIndex]=temp;
}
}
}
}
(6)归并排序:
参考:https://www.jianshu.com/p/33cffa1ce613
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
int[] arr = new int[] {1,3,5,2,4,6,8,10};
System.out.println(Arrays.toString(arr));
mergeSort(arr, 0, arr.length-1);
System.out.println(Arrays.toString(arr));
}
//归并排序(递归思想,从最小一层开始,每一层,先处理左边,再处理右边)
public static void mergeSort(int[] arr,int low,int high) {
int middle=(high+low)/2;
if(low<high) {
//处理左边
mergeSort(arr, low, middle);
//处理右边
mergeSort(arr, middle+1, high);
//归并
merge(arr,low,middle,high);
}
}
public static void merge(int[] arr,int low,int middle, int high) {
//用于存储归并后的临时数组
int[] temp = new int[high-low+1];
//记录第一个数组中需要遍历的下标
int i=low;
//记录第二个数组中需要遍历的下标
int j=middle+1;
//用于记录在临时数组中存放的下标
int index=0;
//遍历两个数组取出小的数字,放入临时数组中
while(i<=middle&&j<=high) {
//第一个数组的数据更小
if(arr[i]<=arr[j]) {
//把小的数据放入临时数组中
temp[index]=arr[i];
//让下标向后移一位;
i++;
}else {
temp[index]=arr[j];
j++;
}
index++;
}
//处理多余的数据
while(j<=high) {
temp[index]=arr[j];
j++;
index++;
}
while(i<=middle) {
temp[index]=arr[i];
i++;
index++;
}
//把临时数组中的数据重新存入原数组
for(int k=0;k<temp.length;k++) {
arr[k+low]=temp[k];
}
}
}
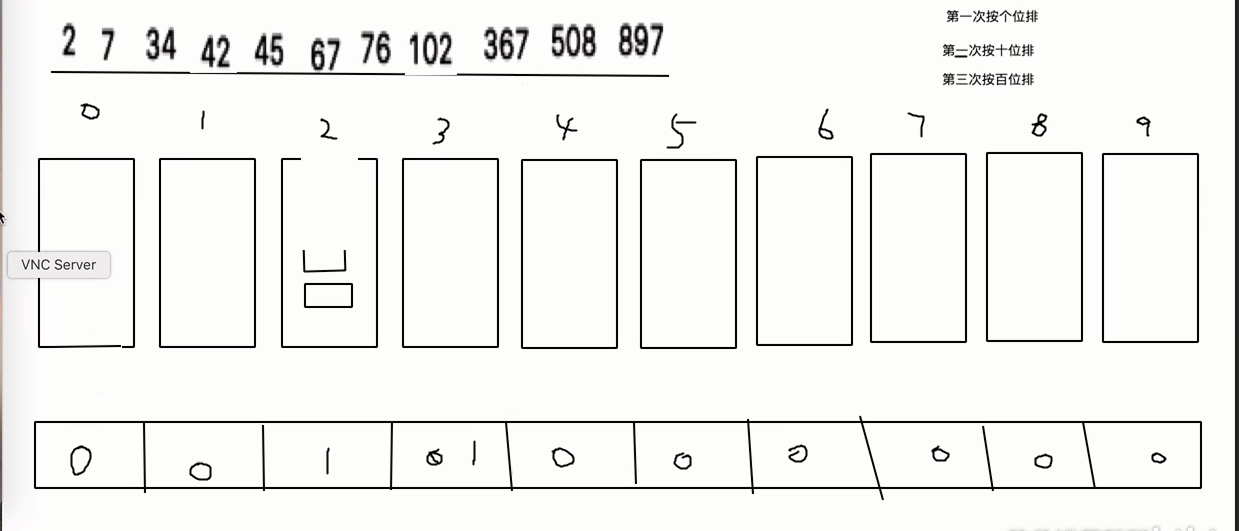
(7)基数排序:
参考:https://www.jianshu.com/p/8340dfaea3af
import java.util.Arrays;
public class RadixSort {
public static void main(String[] args) {
int[] arr = new int[] {23,6,189,45,9,287,56,1,798,34,65,652,5};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr) {
//存最数组中最大的数字
int max=Integer.MIN_VALUE;
for(int i=0;i<arr.length;i++) {
if(arr[i]>max) {
max=arr[i];
}
}
//计算最大数字是几位数
int maxLength = (max+"").length();
//用于临时存储数据的数组
int[][] temp = new int[10][arr.length];
//用于记录在temp中相应的数组中存放的数字的数量
int[] counts = new int[10];
//根据最大长度的数决定比较的次数
for(int i=0,n=1;i<maxLength;i++,n*=10) {
//把每一个数字分别计算余数
for(int j=0;j<arr.length;j++) {
//计算余数
int ys = arr[j]/n%10;
//把当前遍历的数据放入指定的数组中
temp[ys][counts[ys]] = arr[j];
//记录数量
counts[ys]++;
}
//记录取的元素需要放的位置
int index=0;
//把数字取出来
for(int k=0;k<counts.length;k++) {
//记录数量的数组中当前余数记录的数量不为0
if(counts[k]!=0) {
//循环取出元素
for(int l=0;l<counts[k];l++) {
//取出元素
arr[index] = temp[k][l];
//记录下一个位置
index++;
}
//把数量置为0
counts[k]=0;
}
}
}
}
}
(7)基数排序之队列实现:
import java.util.Arrays;
import demo2.MyQueue;
public class RadixQueueSort {
public static void main(String[] args) {
int[] arr = new int[] {23,6,189,45,9,287,56,1,798,34,65,652,5};
radixSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void radixSort(int[] arr) {
//存最数组中最大的数字
int max=Integer.MIN_VALUE;
for(int i=0;i<arr.length;i++) {
if(arr[i]>max) {
max=arr[i];
}
}
//计算最大数字是几位数
int maxLength = (max+"").length();
//用于临时存储数据的队列的数组
MyQueue[] temp = new MyQueue[10];
//为队列数组赋值
for(int i=0;i<temp.length;i++) {
temp[i]=new MyQueue();
}
//根据最大长度的数决定比较的次数
for(int i=0,n=1;i<maxLength;i++,n*=10) {
//把每一个数字分别计算余数
for(int j=0;j<arr.length;j++) {
//计算余数
int ys = arr[j]/n%10;
//把当前遍历的数据放入指定的队列中
temp[ys].add(arr[j]);
}
//记录取的元素需要放的位置
int index=0;
//把所有队列中的数字取出来
for(int k=0;k<temp.length;k++) {
//循环取出元素
while(!temp[k].isEmpty()) {
//取出元素
arr[index] = temp[k].poll();
//记录下一个位置
index++;
}
}
}
}
}
(8)堆排序:
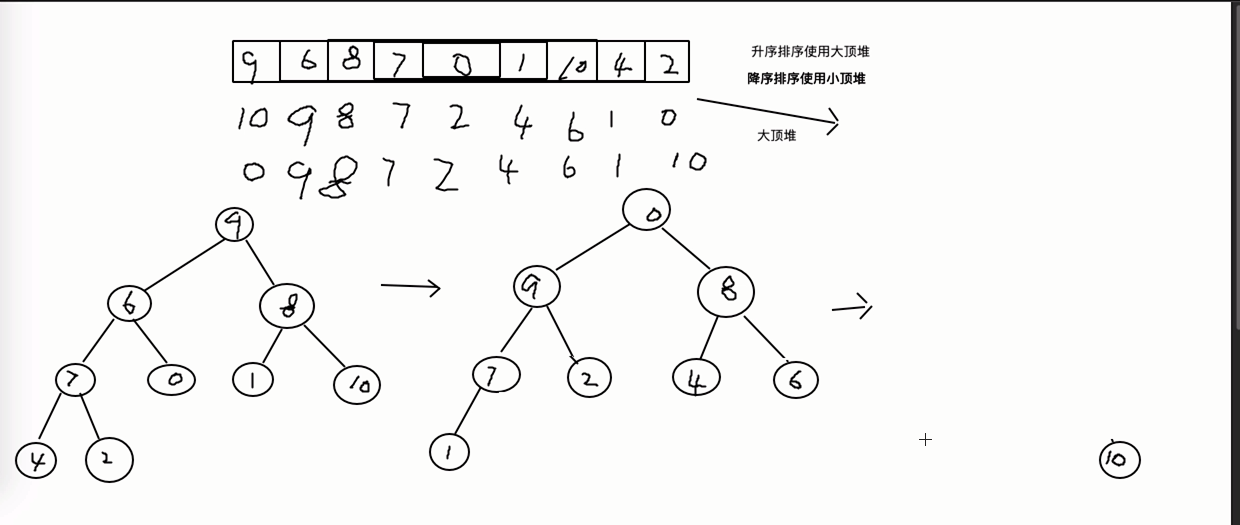
package demo4;
import java.util.Arrays;
public class HeapSort {
public static void main(String[] args) {
int[] arr = new int[] {9,6,8,7,0,1,10,4,2};
heapSort(arr);
System.out.println(Arrays.toString(arr));
}
public static void heapSort(int[] arr) {
//开始位置是最后一个非叶子节点,即最后一个节点的父节点
int start = (arr.length-1)/2;
//调整为大顶堆
for(int i=start;i>=0;i--) {
maxHeap(arr, arr.length, i);
}
//先把数组中的第0个和堆中的最后一个数交换位置,再把前面的处理为大顶堆
for(int i=arr.length-1;i>0;i--) {
int temp = arr[0];
arr[0]=arr[i];
arr[i]=temp;
maxHeap(arr, i, 0);
}
}
public static void maxHeap(int[] arr,int size,int index) {
//左子节点
int leftNode = 2*index+1;
//右子节点
int rightNode = 2*index+2;
int max = index;
//和两个子节点分别对比,找出最大的节点
if(leftNode<size&&arr[leftNode]>arr[max]) {
max=leftNode;
}
if(rightNode<size&&arr[rightNode]>arr[max]) {
max=rightNode;
}
//交换位置
if(max!=index) {
int temp=arr[index];
arr[index]=arr[max];
arr[max]=temp;
//交换位置以后,可能会破坏之前排好的堆,所以,之前的排好的堆需要重新调整
maxHeap(arr, size, max);
}
}
}


