递归、斐波那契数列、汉诺塔
递归:在一个方法(函数)的内部调用该方法(函数)本身的编程方式。

public class TestRecursive {
public static void main(String[] args) {
print(3);
}
//递归
public static void print(int i) {
if(i>0) {
System.out.println(i);
print(i-1);
}
}
}
public class TestFebonacci {
public static void main(String[] args) {
//斐波那契数列:1 1 2 3 5 8 13
int i = febonacci(7);
System.out.println(i);
}
//打印第n项斐波那契数列
public static int febonacci(int i) {
if(i==1 || i==2) {
return 1;
}else {
return febonacci(i-1)+febonacci(i-2);
}
}
}
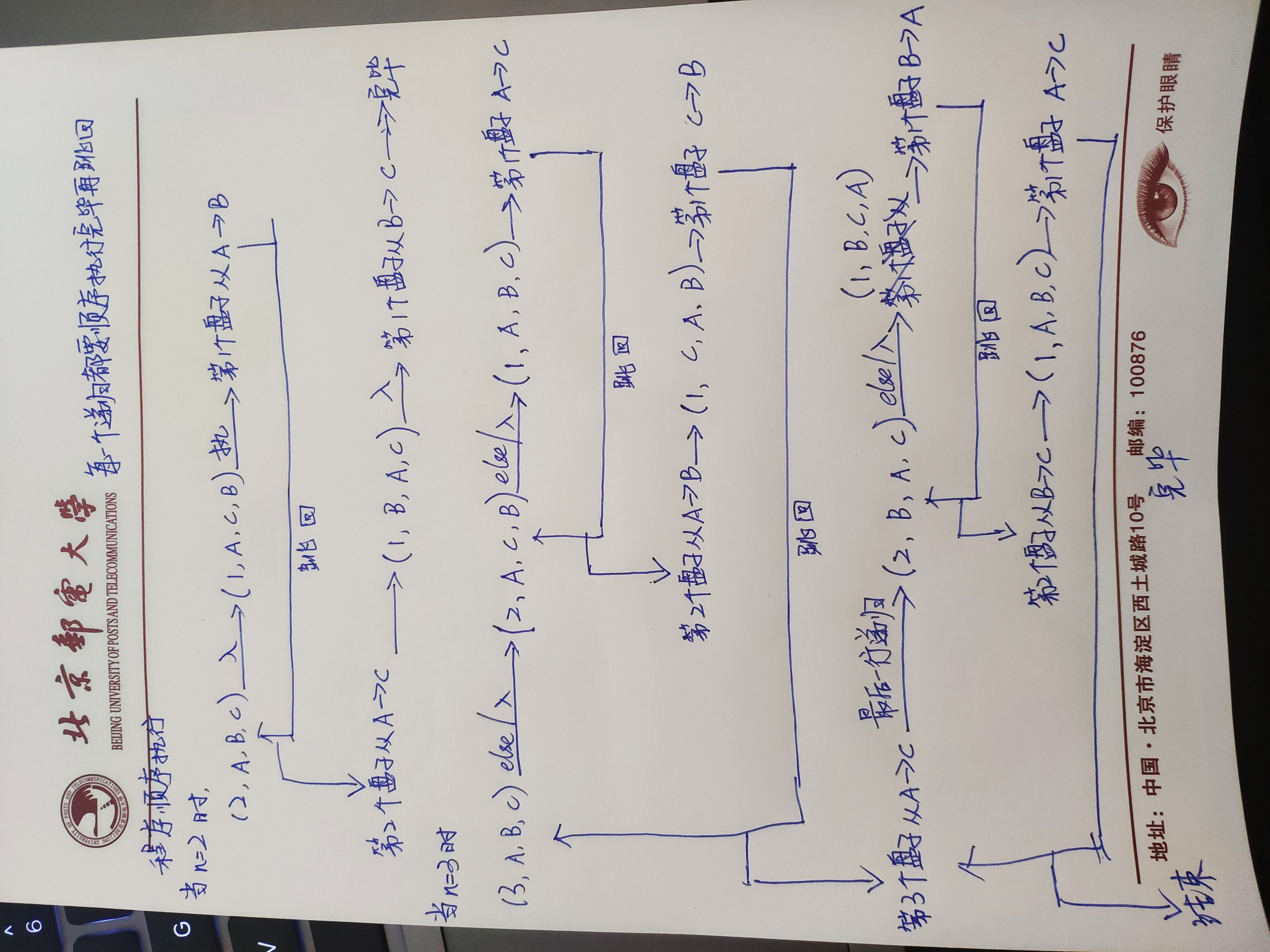
public class TestHanoi {
public static void main(String[] args) {
hanoi(3,'A','B','C');
}
/**
* @param n 共有N个盘子
* @param from 开始的柱子
* @param in 中间的柱子
* @param to 目标柱子
* 无论有多少个盘子,都认为只有两个。上面的所有盘子和最下面一个盘子。
*/
public static void hanoi(int n,char from,char in,char to) {
//只有一个盘子。每层递归执行到n=1结束,跳回各自的顺序执行位置。
if(n==1) {
System.out.println("第1个盘子从"+from+"移到"+to);
//无论有多少个盘子,都认为只有两个。上面的所有盘子和最下面一个盘子。
}else {
//移动上面所有的盘子到中间位置
hanoi(n-1,from,to,in);
//移动下面的盘子,相对于每层递归,最开始传进的实参与形参对应不变
System.out.println("第"+n+"个盘子从"+from+"移到"+to);
//把上面的所有盘子从中间位置移到目标位置
hanoi(n-1,in,from,to);
}
}
}
运行结果:

参考资料: https://baijiahao.baidu.com/s?id=1651515518415910066&wfr=spider&for=pc
分析流程: