聊聊GIS中的坐标系|再版

 

 

目录

• 1. 经纬度与米【告诉大家GIS中的坐标系核心的两种坐标系定义，地理坐标系统vs投影坐标系统】
• 2. 为什么有两种表达（不同点）
• 3. 内在联系（相同点）【指出投影坐标系统的广义定义，即PCS=f（GCS）】
• 4. 常用坐标系统（4.1 WKID；4.2 地理坐标系统；4.3 投影方法；4.4 投影坐标系统；4.5 GCJ02与BD09；4.6 经纬度直投）
• 5. 常用坐标系统的判别与常用软件中的操作（待补充）

---

 

1. 经纬度(例: 119.32°E, 32.48°N)与米(∟, 直角坐标)

让基础浅薄的同学、GIS外行疑惑的，可能就是这两种“单位”的坐标值，以及他们的转换了吧。

2019年是一个不同寻常的年份，大大小小的地震总能被人民日报大V转发。

地震信息一般会带什么呢？

这是一条地震消息，它除了时间、地震等级等消息外，有一个很重要的消息：北纬36.16度，东经98.93度，为了方便，我们用数学的坐标表示法：

点P，P(98.93°E, 36.16°N)

其中，E就是单词East(东)，N就是单词North(北)。

我们先引入两个定义（敲重点）：

• 地理坐标系统（英文简写GCS，Geographical Coordinate System）
• 投影坐标系统（英文简写PCS，Projection Coordinate System）

上述地震点，它用角度值来表示某个点，尽管角度值可以是十进制度，也可以是度分秒（参考初中数学知识）我们说，这种表示空间上的点所用到的坐标参考，叫做地理坐标系统。

与之相对的，用米、千米这种单位表达的，我们在初中数学里很熟悉的，用笛卡尔平面直角坐标系表示的点，我们说它用的是“投影坐标系统”。

注意了！

这个定义是严格的，请用这一组概念继续阅读，我知道读者可能在此之前会看过所谓的“大地坐标系统”、“平面坐标”、“经纬度坐标”等表达，但是，至少在我这里，请用我的这组定义。

我们现在说的，是地理数据的数学基础，即坐标系它自己本身的定义，现在，我说地理数据用的坐标系有“地理坐标系统”和“投影坐标系统”两种，但不止这两种。

2. 为什么有两种表达（不同点）

为什么会有这些差别呢？

我们还要从地球的形状说起。地球是一个近似的椭球，越靠近赤道，越肥。当然，这个“肥”在地球这个尺度下，好几千千米vs20千米，几乎看不出来。

我们GIS是讲究数学的，必须用数学的语言。地球既然是个“椭球”，自然就可以用三维的坐标系统来描述。经纬度，就是解析立体几何里用的“球面坐标系统”。

有好奇的同学会问了，三维坐标有三个坐标值啊，为什么只有经纬度呢？（笑）

在这，我们不画图，也不展开，我在之后的讲解种会展开地理坐标系统的严格定义。但是投影坐标系统的广义定义非常简单，下一节就讲了。

现在，在数学上，只需知道（经度、纬度）是球面坐标系的下的两个分量罢了。

而在地理上，（经度、纬度）则是用角度值表达的“地理坐标系统”的两个分量。

我们拿一个地球仪来看看：

如果初中地理知识过关的话，我认为都能认出：南北极点的经线非常密集，纬线干脆就从赤道的一个大圆变成了一个点。反而越靠近赤道，纬线圈越大，经线圈的距离也越大。

我们计算矩形的面积是怎么计算的了？

S=a×b，a为长边长，b为短边长。

这种“非线性”的变化，就不能用1个经度×1个纬度来表示面积了，因为不同经纬度的地方，1个经度和1个纬度代表的长度并不一样。

正是这个“几何上的计算”的麻烦，所以在计算几何有关值（长度、面积）时，大家更喜欢在【笛卡尔直角坐标系】上计算，也即“投影坐标系统”。

通常，在表示位置的时候，我们喜欢说“xx度东经，yy度北纬”，因为这个基于整个地球，用这简单的两三位数字（不包括小数）就可以精确定位到地球的任意一点。

而在局部某个地区，可以是某个市的行政区，某个省的某几个市，我们喜欢用平面直角坐标来计算长度、面积。

这就是“地理坐标系统”和“投影坐标系统”的一个最原始的需求差异。

事实上，用角度来计算面积在高等数学中并非难事，但是，能用S=a×b来算，先人就不会用复杂的表达式了。

所以，

既然一个擅长定位，一个擅长计算，二者是如何联系在一起的呢？

是啊，我们只有一个地球，但是可以用不同的表达方法（没错，就是坐标系统）来描述同一个地方，坐标系这个小东西确实让一些人头疼啊。

3. 内在联系（相同点）

上来开大，投影坐标系统的广义定义如下：

投影坐标系统 = f(地理坐标系统)

我们说，投影坐标系统是基于一个法则f和一个地理坐标系统而定义的。

这个定义是一个广义定义，有更精确的定义于以后讲解。

• 法则f：学名“投影方法”，简称“投影”
• 地理坐标系统：非精确定义见上文

为什么球面坐标（角度值）能通过一个投影方法f计算得到平面直角坐标（千米、米）呢？

如何以曲化直呢？

这得得益于数学家的功劳，赶紧给高斯、牛顿、莱布尼茨、拉格朗日、欧拉这些大佬烧香啊~

举个最简单的例子，在平面上，用角度+长度表达的极坐标就能通过一组简单的公式换算到平面直角坐标：

• x=R×sin∠A
• y=R×cos∠A

具体定义不扯太远，但是，这个法则f远远比这两个公式复杂得多。

在这里，只需记住，一个投影坐标系统，必然包括一个投影方法和一个地理坐标系统的定义。

那么，

• 投影方法有哪些呢？
• 地理坐标系统有哪些呢？
• 基于某个地理坐标系统，又有哪些投影坐标系统呢？
• 在软件上又是如何识别和计算、操作的呢？

死亡四连问啊，没关系，马上解答。

4. 常用坐标系统

4.1. 一对名词：WKID与EPSG

WKID即Well Known ID，众所周知的ID号的意思。EPSG是管理这些ID号的一个组织，网站是epsg.io

通常来说，一个GIS里的坐标系统，必须有一个WKID，某些特别的除外，下面会讲。

例如，WKID=4326，即WGS84这个地理坐标系统的ID。

注意！！！

地理坐标系统和投影坐标系统均使用这套定义，但是不会重复，也没有规律说哪一段数字是地理坐标系统，哪一段是投影坐标系统。

幸运的是，我们并不需要完全记完，网上这个WKID大全列表很容易找到，而且只需记住项目中用的、以及常见的即可。

4.2. 常见地理坐标系统及WKID

①WGS84（WKID=4326）

美国GPS使用的一个全球地理坐标系统，osm地图、谷歌地图（国外版）、Landsat系列卫星影像图等均在地理坐标系统上使用了这个，有许多开发地图的api默认是使用WGS84的，WGS84使用极其广泛。

全称 World Geodetic System 1984。我们在网上交流的数据大多数也是WGS84的，毕竟osm地图是开源免费的，任意下载。

需要注意的是，加密前的高德、百度用的也是WGS84，有关高德百度等常见国内电子地图的坐标系统，在4.5节会详细介绍。

②CGCS2000（WKID=4490）

我国的GPS系统-北斗导航系统以及国家发行的“天地图”，用的是这一套地理坐标系统，中文名“中国国家2000地理坐标系统”，英文全称翻译名“中国大地坐标系2000”。

英文名 China Geodetic Coordinate System 2000。

③北京54、西安80

是我国已经逐渐停止使用的两个地理坐标系统。

北京54坐标系统WKID是4214，西安80坐标系统的WKID是4610。

尽管有大量历史遗留数据仍采用这两个坐标系统，作为学习研究使用当然是可以的，但是建议尽快转移到国家2000坐标系来（转换方法暂且不说，以后会说）。

小补充：

北京54是建国初，在当时技术条件不高时“引”苏联的地理坐标系统到我国境内的，在地理坐标系统的精确定义时会详细展开为何北京54在我国境内为何有较大偏差。

而西安80则是改革开放后，技术稍好，为解决北京54偏差问题，为我国各项事业发展搞的一个适用于国内的地理坐标系统。

为什么会启用国家2000呢？也留到以后地理坐标系统的精确定义来谈，感兴趣的朋友可以等等我。

④美国常用地理坐标系统

NAD27、NAD83

4.3. 常见投影方法

什么是投影？这里，待投影的“东西”是地球表面这个曲面——投影到哪里？假如地心有一个灯泡，灯泡的光线能把地表照射到一个面上，而这个面可以展开成为平面，我们说投影到的这个面，叫投影面。

 

（网络图，灯光将物体投影到墙面这个平面，墙面与物体呈垂直方向，即纵轴投影）

事实上，能展开成平面的面有平面本身、椭圆柱面、圆锥面（好像就见过这仨）等。根据投影面和地球的相对位置，可以有非常多种投影方法。

①高斯克吕格（Gauss - Kruger）

高斯克吕格是由高斯和克吕格两人一起搞的投影法则，投影面是一个椭圆柱面打横着套在地球的数学椭球面上，围绕地轴旋转，将地球表面投影到该椭圆柱面的一种投影方法。

不懂？看图：

 

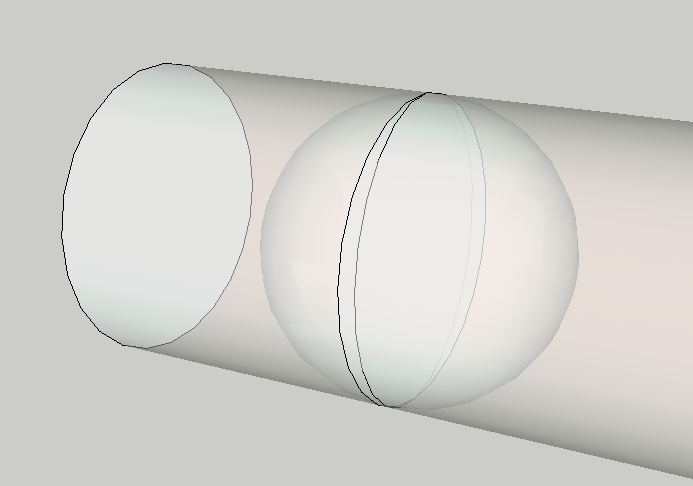
以某条经线与椭圆柱面相切（这条经线就叫中央经线），投影到椭圆柱面后，再沿着椭圆柱面的高剪开摊成平面，就是高斯投影的原理啦。

高斯克吕格投影是分带的，经度不是有东西各180度吗？所以可以按3度或者6度剥开一瓣用于投影。

 

旋转高斯克吕格的投影面，可以获取下一个分带的投影，以合适全球所有的地方。

请读者发挥一下想象力，因为从图上看，越远离中央经线的地方投影到椭圆柱面上，变形越严重，反而是中央经线附近的地方非常能贴合投影面。

--- 如果不懂也没关系，我们已经能给出高斯投影的学名了：横轴（因为投影面是躺着的 与地轴垂直）切（因为与地表面是相切关系）椭圆柱（投影面是椭圆柱面）投影。

实际上，高斯克吕格投影也叫“横轴墨卡托投影”，因为投影面是（椭）圆柱面的投影均叫“墨卡托投影”，见第②点。

②墨卡托投影（Mercator）

墨卡托发明的投影叫墨卡托投影，特点是纵轴，即投影面是个圆柱，与地球赤道相切（立着的水管里塞了个乒乓球），学名：正轴切圆柱投影。

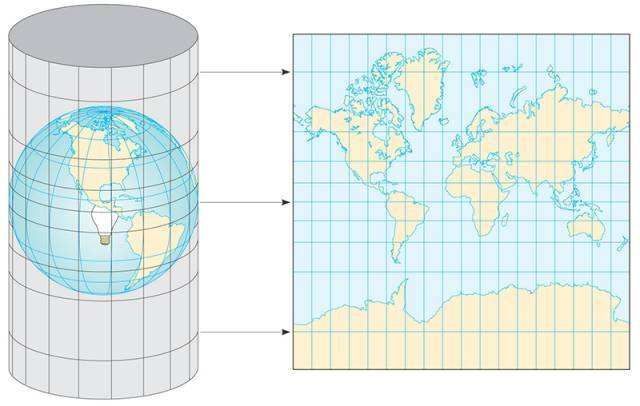
 （网络图片）

③UTM投影（Universal Transverse Mercator）

全称“通用横轴墨卡托投影”，和高斯克吕格投影非常相似，只不过它并不是切于经线圈，而是穿地球而过。我们从侧面来看，高斯投影面和经线圈是完全重合的，但是UTM则不是：

（网络图片，很复杂，但很形象）

UTM投影是贯穿地球的，应该是侧面上看相割。

UTM投影为美国陆军工程兵测绘局于20世纪40年代提出。当时对美国本土采用Clarke 1866椭球体，对全球其它地方采用其他椭球体。

UTM投影现在采用WGS84地理坐标系统进行投影。

现在，很多遥感影像图用的就是UTM投影出来的投影坐标系统。

③网络墨卡托（WebMercator）

Web Mercator投影不是严格意义的墨卡托投影，而是一个伪墨卡托的投影方法，这个伪墨卡托投影方法的大名是 Popular Visualization Pseudo Mercator，PVPM。

因为这个投影方法是Google Map最先发明并使用的。

它的地理上的不严谨性在于，在投影过程中，将表示地球的椭球面作为正球面处理。

传说中是因为谷歌程序员懒得用椭球面来编程计算屏幕坐标...

有关网络墨卡托，还有一段更有趣的故事，见参考文献。

④兰伯特（Lambert）投影与阿尔伯斯（Albers）投影

兰伯特投影，投影面是圆锥面，更像是一个圆锥筒子套在一个球上（图a）：

此时的兰伯特投影是切圆锥投影，当然兰伯特也可以是割圆锥投影（图b）。

它类似于阿尔伯斯投影，不同之处在于其描绘形状比描绘面积更准确。

中国国家全幅地图、美国国家平面坐标系对所有具有较大东西范围的区域均使用此投影。国际上用此投影编制1∶100万地形图和航空图。

而阿尔伯斯投影常见于我国的省区投影，因为面积更准确。

阿尔伯斯投影是一种圆锥等面积投影。

* 补充：兰伯特投影还有另外一种投影方法，投影面并不是圆锥面，而是平面。见维基定义上的图：

4.4. 常见投影坐标系统及WKID

①基于高斯克吕格投影的投影坐标系统族

在我国，基于北京54、西安80、国家2000，均可以使用高斯克吕格投影定义出投影坐标系统。

因为地理坐标系统有这三个（实际上高斯克吕格投影在别的国家也有应用，不过这里只讨论我国），加上高斯克吕格投影方法允许分带表达，

所以，该投影坐标系统族有很多个，以WKID=4547为例。

WKID=4547这个投影坐标系统是这样定义的：

地理坐标系为国家2000坐标系，使用3度分带规则，中央经线为东经114°，使用高斯克吕格投影的投影坐标系统，并且平面坐标系统的经度方向上的Y坐标值无投影带号。

简写为：3度投影带114°中央经线的高斯投影坐标系统（2000坐标不带带号）。

坐标值若不带带号的投影坐标系统会产生重叠。那么带带号的呢？WKID=4526正是WKID=4547这个带带号的PCS对应的有带号的投影坐标系统。

在ArcGIS中，区分有无带号，从投影坐标系统的名称中可以看出：

• CGCS2000_3_Degree_GK_CM_111E：名称中有CM，在Y坐标（经线方向）不带带号
• CGCS2000_3_Degree_GK_Zone_30：名称中有Zone，则在Y坐标（经线方向）带带号
• Beijing_1954_3_Degree_GK_CM_111E：（同上）
• Beijing_1954_3_Degree_GK_Zone_35：（同上）
• Xian_1980_3_Degree_GK_CM_111E：（同上）
• Xian_1980_3_Degree_GK_Zone_34：（同上）

带带号就是在Y坐标值前多加投影带数字，例如，某第38投影带上的不带投影带的坐标值为（494832，2546025），则带投影带的坐标为（38494832，2546025）

以上为国家2000、北京54、西安80在“GK投影（高斯克吕格投影）”下同一中央经线，坐标值内带投影带与不带投影带投影坐标系统的名称。

总结：常用的高斯投影的PCS族，在我国，地理坐标系统只有北京54、西安80、国家2000，根据中央经线按需选用。

②基于UTM投影的投影坐标系统族

和①中高斯投影坐标系统族类似，只不过仅仅基于WGS84。

分带与名称不再赘述，按中央经线自行使用即可。

③基于网络墨卡托（WebMercator）的投影坐标系统

只有一个，WKID=3857。

有趣的是，网络墨卡托投影坐标系统还有102100、900913这俩ID，有兴趣的朋友可以看参考文献里的《Web Mercator 公开的小秘密》一文。

当前，我国的高德、百度、腾讯地图，谷歌地图（国内国外均）、osm地图都用了网络墨卡托来平面化展示，只不过国内高德百度腾讯和国内谷歌地图的地理坐标系统经过加密，加密知识见4.5节。

而天地图虽然用的是国家2000地理坐标系，但是也提供了墨卡托投影方法来展示平面地图。

ArcGIS Earth这个免费的小软件则直接使用3857坐标系（和Google Earth类似）。

④基于兰伯特与阿尔伯斯的投影坐标系统

时间原因，此处暂不列举WKID，总之我国大公鸡图喜欢用阿尔伯斯投影，我国省区图喜欢用兰伯特圆锥投影。

⑤不常见投影坐标系统

我国因部分地区建设需求，自己给自己定义了投影坐标系统，在我的实践经验中，见过的有：NJ08坐标系（基于CGCS2000）、广州地方坐标系（基于CGCS2000）等。

4.5. 假坐标系统：GCJ02与BD09

在4.4节的第③点中已经提及，国内高德、百度、腾讯和国内谷歌地图的地理坐标系统均经过加密。

它们使用的都是WGS84坐标系（坊间传）。

因为国家保密需要，网络地图至少要用一种特殊的算法进行加密，那就是大（e）名（chou）鼎（bu）鼎（kan）的加密算法——GCJ02。（当然，天地图没有加密，直接是CGCS2000）

民间也叫火星坐标系，它加密后的WGS84坐标，与真实的WGS84坐标是有误差的，这个误差值并不固定，通常是几十米到几百米。

GCJ02加密算法是一种多项式+正弦函数加密算法，通常隔一段时间就换一下参数，所以，网上所谓的解密算法并不是官方的精确算法，隔一段时间说不定就不准确了。

有关WGS84和GCJ02，可以查阅参考文档里的《关于GCJ02和WGS84坐标系的一点实验》，出自李民录。这里摘抄一张图，是我国各个地区GCJ02加密后的不同偏移值：

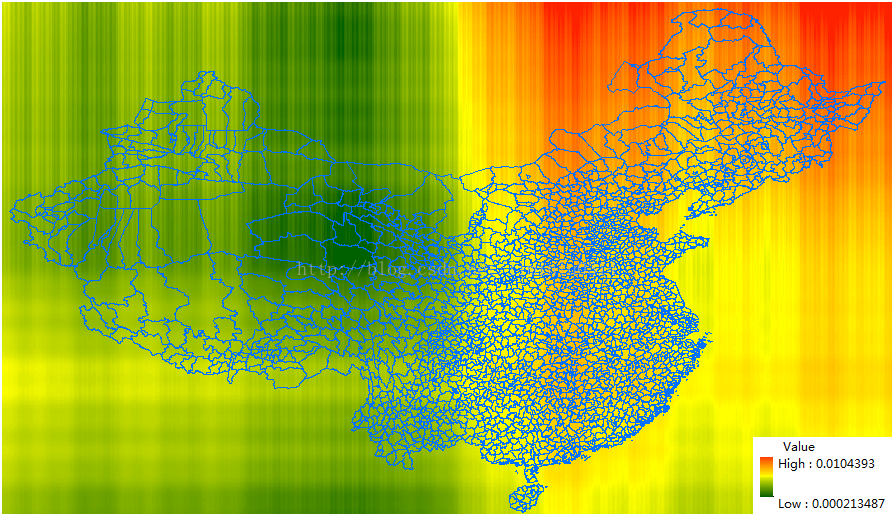
百度地图更为恶心，在GCJ02的基础上再次偏移，也就是BD09。

这个加密算法并不公开，需要找有关部门交钱审核才能获取，而且没有精确的反向算法（多项式咋反向啊）。

所以，知道为什么说GCJ02/BD09是“假的坐标系”了吧？

4.6. 经纬度直投

这是一个非常恶心的做法，即把经纬度等同直角坐标来绘制，这样就有一个后果：

当纬度=90度时，理论上有无限个点（即经度有无限个），若经纬度=直角坐标，那么赤道有多长，极点就展开拉的有多长。

这种拉扯是非常恶心的，天地图就这么干，在我国高纬度地区，使用经纬度直投的绘制方法，会使得本来直角相交的两条道路斜变：

 

  

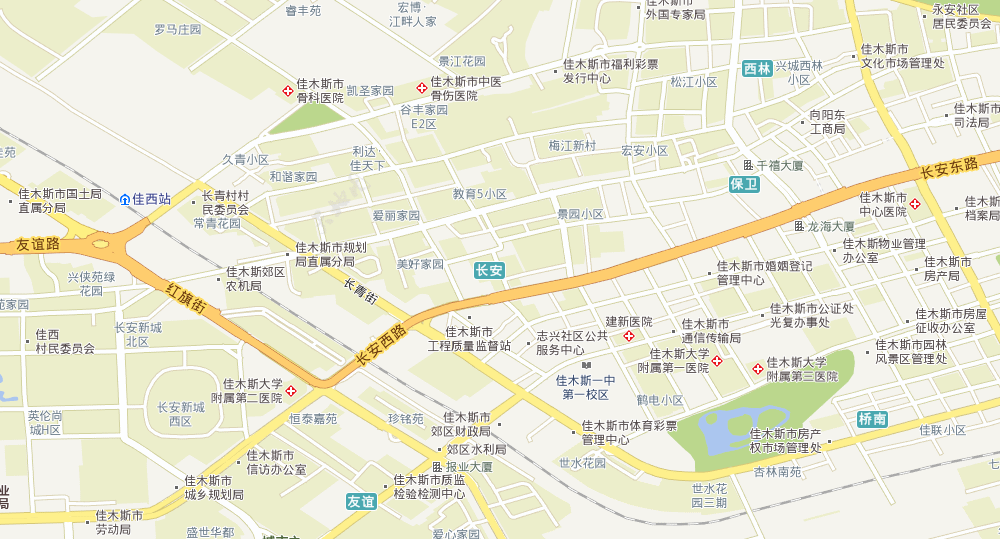
（天地图，黑龙江佳木斯市两种投影的对比，上图为经纬度直投）

这也是ArcMap的默认“投影”，通常比较丑，尤其是高纬度地区变形非常严重，但是胜在渲染速度快。

5. 常用坐标系统在软件中的判别与操作

5.1. 判别（具体问题具体分析）

• 如果数据有坐标系统的定义，则可以从数据的坐标系统中得知坐标系（假如定义的正确）。
• 如果数据没有坐标系统定义，需要通过观察数据坐标值来判断GCS、PCS类型，则需要一定的经验。
• 如果数据是两位数+三位数或者三位数+三位数等落于我国经纬度范围的数字，则可以大致判断是地理坐标系统，只需询问数据提供者，然后自己为数据定义地理坐标系统即可。
• 如果给的数据尺度很小，例如是一个厂房，而且一个单位数值差不多就是1米，则判断是CAD绘图，是未经校准的平面直角坐标系，可以理解为投影坐标系，只不过位置并不准确罢了，需要校准。
• 如果给的数据单位很大，通常是几万、几十万（5位数+6位数，是无投影带的，5位数是经线x方向，6位数是纬线y方向）（6位数+7位数，是有投影带的，6位数是纬线y方向，7位数是经线x方向，通过7位数的前两个数字判断投影带），此时可以粗略判断是投影坐标系统。
• 如果均不是以上的数值，则判断为误操作，可能是错误定义了坐标系，也可能是错误进行投影计算。

5.2. 操作：以主流软件为例

①ArcMap

简单讲一下，在arcgis - arcmap中，在数据管理工具箱>投影工具集下，是处理坐标系统的强大工具。

“定义投影”工具，是为无坐标系统定义的数据定义GCS或PCS用的；

“投影”工具，是转换坐标系统用的，可以由GCS投影到指定PCS，也可以由PCS转到指定GCS（可以是PCS定义内的GCS，也可以是其他GCS），也可以由PCS转到另一个PCS（换投影带，或者连GCS、PCS一起换）

>注意，跨GCS的“投影”操作，需要“地理转换”辅助，有关地理转换，会专门出一篇博客讲解。

“投影栅格”工具，是转换栅格数据用的，用法同“投影”工具。

以后放图及其他软件的操作。