十四、降维 (Dimensionality Reduction)
14.1 动机一:数据压缩
本小节主要介绍另外一种无监督学习方法:dimensionality reduction,从而实现数据的压缩。这样不仅能够降低数据所占磁盘空间,还能够提高程序的执行速度。例如以下图所看到的的样例,如果有一个具有许多维特征的数据集(尽管下图仅仅画出2个特征),能够看到x1以cm为单位,x2以inches为单位,它们都是測量长度的。所以,给出的数据是很冗余的,应该把这两维数据降到一维(这样的情况是常见的。比如,採用两种不同的仪器来測量一些物体的尺寸。当中一个仪器測量结果的单位是英寸,还有一个仪器測量的结果是厘米。这样的情况在project中是常常会发生的,有时可能有几个不同的project团队,第一个project队给出二百个特征。第二个project队给出另外三百个的特征,第三个project队给出五百个特征,这些特征放在一起很的多,而且可能会出现一些冗余)。
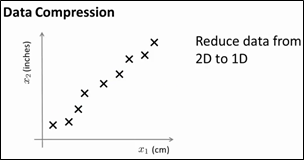
怎样将2D数据降到1D?降维,就是希望找到例如以下图所看到的的直线,全部的点映射到这条直线上,这个新特征叫做z1,要确定点在这条直线上的位置,仅仅须要一个数字就可以。
比如。表示原来的样本x(1)须要两个数字或者是一个二维向量,降维后,用z(1)就能够表示这个样本。总结一下,假设能够将原数据集中的全部数据都映射到一条直线上,用映射后的数据来近似原来的数据集,那么,仅仅须要一个实数来确定某个点在直线上的位置。所以。如今仅仅须要为每一个样本保留一个数字。
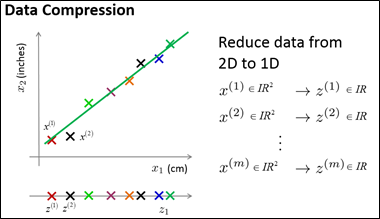
以下。给出一个将数据从三维降至二维的样例。例如以下图所看到的(在实际应用中。可能具有10000维的特征。须要降到100维。这里仅以3D降到2D为例),给出了一个数据集,每一个样本有三个特征。全部这些数据点可能都能差点儿相同经过一个平面,所以,将全部这些数据点都投影到这个二维平面上,为了表示某个点在平面上的位置,须要两个数,降维后,利用z1、z2表示每一个样本。下图中分别给出了3D数据、降维后的2D数据和降维后的2D数据的鸟瞰图。
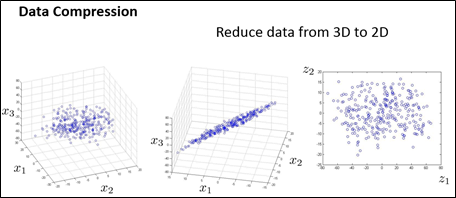
14.2 动机二:数据可视化
本小节将主要解说降维的另外一种应用,即数据的可视化。很多机器学习算法可以帮助我们开发高效的学习算法,但前提是我们可以更好地理解数据。数据降维是可以将数据可视化的一种实用的工具。假如我们已经搜集了大量的数据,具有很多的特征。如x∈R50。那么,怎样可以将这些数据可视化呢?绘制一幅50维的图是不可能的。
那么,有没有可以观察数据的好方法呢?可以使用降维方法,比如。可以利用两个数总结50个特征。
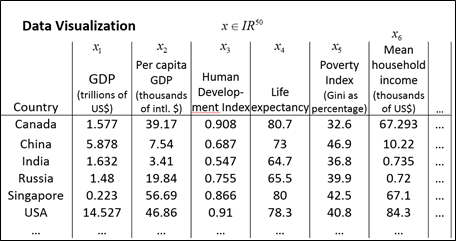
假使我们有关于很多不同国家的数据,每个特征向量由50个特征构成(如。GDP,人均 GDP,平均寿命等)。假设要将这个50维的数据可视化是不可能的。假设可以使用降维的方法将其降至2维,便可以将其可视化了。
这样做的问题在于,降维算法仅仅负责降低维数。而新产生的特征的意义就必须由我们自己去发现了。
14.3 主成分分析问题
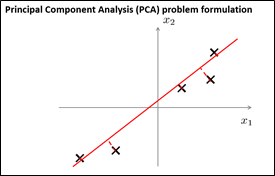
对于降维问题来说,眼下最流行、最有用的方法是主成分分析法(Principal Componet Analysis, PAC)。本小节主要介绍PCA的公式描写叙述。如果有下图所看到的的数据集,该数据集中含有二维实数空间内的样本x,如今,须要对数据进行降维。由2D降到1D。想找到一条直线。把全部数据点都投影到该直线上,那么。怎么可以找到这样一条直线呢?例如以下图所看到的,事实上就是想找到一条直线,使得全部数据点到它们在这条直线上的投影点之间的距离的平方和最小,这些距离被称为投影误差。所以,PCA的目的就是为了寻找到一个投影平面。使得投影误差平方和达到最小。在进行PCA之前。须要先进行数据归一化和特征规范化,使得x1、x2的特征均值为0。
仍回到刚刚的问题,如今,如果选择另外一条投影直线。会发现结果非常的差,由于投影误差非常大,每一个样本都须要移动非常大的距离才干被投影到这条投影直线上。这也就是为什么PCA会选择第一条直线作为投影直线。
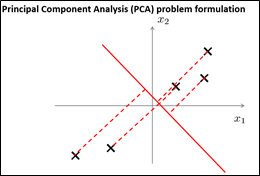
在PCA中,我们要做的是找到一个方向向量(Vector direction),当我们把全部的数据都投射到该向量上时,使得投射平均均方误差能尽可能地小。方向向量是一个经过原点的向量。而投影误差是从特征向量向该方向向量作垂线的长度,而且,与方向向量的方向无关。主成分分析问题的描写叙述:问题是要将n维数据降至k维,目标是找到向量u(1), u(2),..., u(k)使得总的投影误差最小。

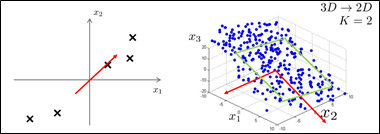
对于3D降到2D的目的就是:找到两个方向向量。它们能够确定一个2D平面,全部3D数据点到该2D平面投影误差平方和最小。
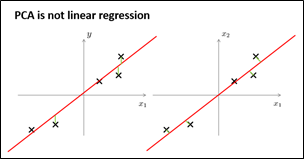
主成分分析与线性回归之间有什么关系呢?主成分分析与线性回归是两种不同的算法,它们仅仅是看起来有点类似。
主成分分析最小化的是投影误差(Projected Error)。而线性回归尝试的是最小化预測误差。
例如以下图所看到的。左边的是线性回归的误差(垂直于横轴投影)。右边则是主要成分分析的误差(垂直于红线投影)。线性回归的目的是预測结果,而主成分分析不作不论什么预測。
PCA是在寻找一个低维的平面,使得数据在其上的投影具有最小化的投影误差平方和。
14.4 主成分分析算法
本小节開始介绍主成分分析算法。即它的实现过程。在进行PCA之前,须要先进行一个数据预处理过程,拿到一组具有m个无标签样本训练集,一般先进行归一化处理,然后,因为不同特征的取值范围不同。须要进行特征缩放。

PCA的主要目的就是求解k个方向向量和全部数据点在投影后的低维面的投影点。
以下给出PCA的步骤:
(1)数据归一化和特征尺度缩放。
我们须要计算出全部特征的均值(即全部样本每一维特征的均值),然后令xj= xj -μj(每个样本的特征向量-特征均值向量)。
假设特征是在不同的数量级上,须要将其除以标准差σ。
(2)计算全部数据点的协方差矩阵Σ(covariance matrix):

(3)计算协方差矩阵Σ的特征向量(eigenvectors):
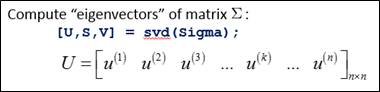
(4)对于一个 n×n维度的矩阵,上式中的矩阵U的各列是使得已知数据具有最小投影误差的方向向量。假设我们希望将数据从n维降至k维。仅仅须要从U中选取前k个向量。获得一个n×k维度的矩阵。用Ureduce 表示,然后通过下式获得要求的新特征向量 z(i):
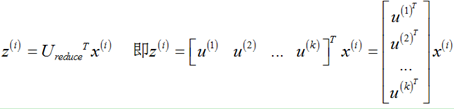
当中x(i)是n×1维的,因此结果z(i)为k×1维度。注: PCA不考虑x0=1。
14.5 选择主成分的数量
在PCA算法中,将n维特征变量变换为k维特征变量,这里的參数k是一个重要的參数,被称为主成分的数量,本小节主要讲述怎样选择这个參数k。首先,给出几个概念。
(1)投影误差平方和均值(average squared projection error):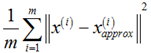 ,当中,
,当中,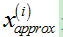 是
是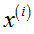 在降维平面上的投影点,
在降维平面上的投影点,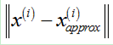 是
是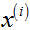 和
和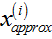 之间的距离;
之间的距离;
(2)数据总变差(Total variation in the data):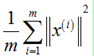 。即数据集中全部样本长度的平方和的均值,也就是,平均来看。样本距离原点有多远;
。即数据集中全部样本长度的平方和的均值,也就是,平均来看。样本距离原点有多远;
选择k值时。一个经验法则是:选择使以上两个数据(投影误差平方和均值、数据总变差)之间的比例≤0.01的最小k值,所以。在选择k值时,重要的是选择0.01这个数还是其它的数字。假设选择0.01。则表示保留了99%的差异性(这是PCA的语言)。假设选择0.05,则表示保留了95%的差异性;选择0.1,表示保留了90%的差异性,这些都是比較典型的数值。这样,在保证降维的基础上,还能保留大部分的差异性。
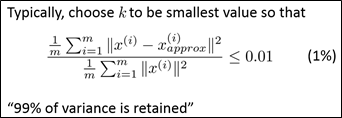
那么,假设实现这个过程呢?首先,令k=1。进行PCA。然后。计算样本投影误差平方和均值与数据总变差之间的比值。假设满足范围要求,则停止。k=1就是比較好的选择。否则,接下来尝试k=2。知道满足要求为止。但这个过程效率比較底下。要一个个去尝试,实际上。在进行PCA时,在对协方差矩阵进行svd时。还会得到一个矩阵S,它是一个维数为n的正方阵。能够证明。给定一个k值,样本投影误差平方和均值与数据总变差之间的比值能够由下式计算得到:
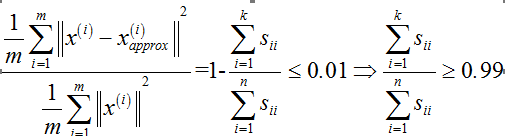
所以。在对k值进行尝试时,仅仅须要计算上式就可以,从而逐渐找到可以确保99%差异性被保留的最小k值。这样做。仅仅须要调用一次svd,而不是一遍一遍调用svd。

总结一下。在利用PCA进行数据压缩时。通常使用的方法是:对协方差矩阵进行一次svd,然后找到使得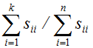 满足要求的最小k值。
满足要求的最小k值。
(在解释PCA获得比較好性能的这个数字时。应该说"有百分之多少的差异性能被保留下来了",表明了这些近似数据对原始数据的近似有多好)

14.6 重建的压缩表示
PCA作为数据压缩算法,它能够把1000维的数据压缩100维特征,或将3D数据压缩到2D。
有这样一个数据压缩方法,那么对应地也应该有一个算法能够将压缩过的数据近似地变回到原始的高维度数据。
如果有一个已经被压缩过的z(i),它有100个维度,如何将它变回到原始的1000维的x(i)呢?
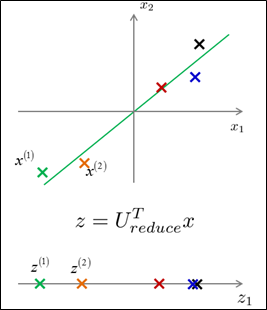
例如以下左图所看到的,给定一组2D样本。将它们降维到1D。如今,假设利用这些1D数据恢复出原来的2D数据呢?因为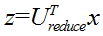 ,那么,能够
,那么,能够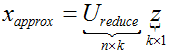 ,依据PCA,投影误差平方和不会非常大,所以,
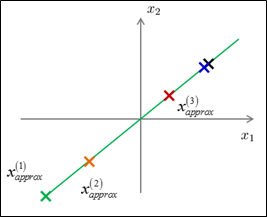
,依据PCA,投影误差平方和不会非常大,所以, 会比較接近于x。例如以下右图所看到的。
会比較接近于x。例如以下右图所看到的。
14.7 主成分分析法的应用建议
如前面所述,PCA能够提高机器学习算法的速度,本小节主要讲述在实际应用中怎样实现PCA。怎样通过PCA提高学习算法的效率呢?如今有一个监督学习问题。训练样本为输入的x和标签y,假设样本x(i)的维度很高,比如,x(i)∈IR10,000,在计算机视觉问题中。有一张100×100的图像,假设以全部像素点的强度值作为特征。则会得到一个特征维数为10,000的特征向量,这样的维度很高的特征向量,执行速度很慢。须要进行降维,详细方法例如以下:
从训练集中提取出x(临时不考虑y,相当于得到一组无标签的训练集),利用PCA从中得到一组降维的数据。这样。得到一组新的训练集。同一时候,将原有的标签增加。然后,将已经降维的数据集输入到学习算法中。假设有一个新的样本x,对它的类别进行预測,那么,须要利用PCA对其进行降维,然后利用学习算法得到的分类器对其进行分类。

PCA的主要应用为:数据压缩(Compression)、数据可视化(Visualization)。
以下,介绍PCA常见的错误。有人用它来进行过拟合的控制,这不是一个好的应用,由于。PCA并不须要标签,它把某些特征舍弃掉了。

另一个关于PCA的误用。比如,在设计机器学习算法时。有人会进行例如以下操作,在项目的初期使用PCA,但这不是非常恰当。在使用PCA之前,应该先用原始数据进行学习,在确定原始数据确实不是非常好的时候,再去考虑PCA,而不应该在没有对原始数据进行学习时,就直接使用PCA。




